Гидравлический расчет трубопроводов
Основной задачей гидравлического расчета является определение диаметра d трубопровода и потери напора h по заданной производительности Q (объемному или массовому расходу). Расчет вновь проектируемого трубопровода начинают с предварительного выбора диаметра и ориентировочно выбранной скорости движения жидкости [51, 60]. Рекомендуемая скорость в напорном трубопроводе зависит от вязкости нефтепродукта и выбирается в пределах 1 – 2,5 м/c. Чем меньше вязкость нефтепродукта, тем больше его скорость. Основным свойством жидкости, влияющим на давление и производительность перекачки, является вязкость, характеризующая собой внутреннее трение жидкости. В формулах гидравлики трубопроводов обычно фигурирует кинематическая вязкость, измеряемая в квадратных метрах на секунду (м2/с), в стоксах (см2/с), или сантистоксах (мм2/с). Динамическая вязкость измеряется в (Н/м2)∙с или Па∙с (Паскаль – секунда). Для перевода кинематической вязкости в динамическую ее значение в м2/с необходимо умножить на плотность в кг/м3. По скорости В гидравлике различают два основных режима движения жидкости – ламинарный (спокойный) и турбулентный (вихревой). При ламинарном (lamina – лат. слой) движении частицы жидкости движутся без перемешивания. Примером ламинарного движения может быть перемещение нефти в трубе. При турбулентном (turbulentus – лат. вихревой) частицы жидкости движутся с завихрениями, имея сложные траектории. На вихреобразование затрачивается часть энергии потока жидкости, что приводит к большим потерям. Режим движения жидкости определяют по числу Рейнольдса:
где Установлено, что при Re > 2320 в трубопроводе кругового сечения всегда имеет место турбулентный режим, а при Re < 2320 – ламинарный. Для труб произвольного сечения вместо диаметра d подставляют значение, равное 4 Rг. Величина Rг = Перемещение жидкости связано с потерей напора. Потери напора зависят от величины скорости движения жидкости и пропорциональны скорости в квадрате. Напор – это энергия, отнесенная к единице веса. Напор измеряют единицами длины (м, см, мм). Различают напор геометрический, пьезометрический и скоростной. Геометрический напор зависит от высоты положения, например, резервуара. При подъеме резервуара с жидкостью плотностью 1000 кг/ м3 на высоту 10 м в шланге (трубопроводе) на плоскости сравнения (у основания) будет действовать избыточное давление 0,98∙105 Н/м2 (1 атм.). Пьезометрический (пьезо – греч. давлю) напор зависит от величины давления, действующего на стенки трубы со стороны жидкости (газа). Пьезометрический напор определяют из выражения При перемещении жидкости по трубопроводам насос должен развивать напор, необходимый для преодоления гидравлических сопротивлений трения по длине трубопровода; местных сопротивлений (вентили, изгибы, повороты); геометрической высоты, равной разности отметок уровней жидкости в конечном и начальном пунктах перекачки, а также на создание скоростного напора жидкости (свободного напора на выходе). Величина потери напора на трение по длине для труб круглого сечения выражается следующим уравнением гидравлики, предложенным учеными Дарси и Вейсбахом в 1755 г. [37, 61]:
где Потерю напора можно выразить через объемный расход, который определяется выражением:
где F – площадь трубы. Определив значение
Гидравлический уклон:
где Под шероховатостью понимают неровности (выступы) внутренних поверхностей стенок. Различают естественную и эквивалентную шероховатость. Эквивалентная (усредненная) шероховатость Значения эквивалентной шероховатости для стальных и чугунных труб следующие: 1. Стальные новые – 0,02 – 0,1 мм. 2. Стальные, находящиеся в эксплуатации, до 1,0 мм. 3. Чугунные новые – 0,25 – 1,0 мм. 4. Чугунные, находящиеся в эксплуатации, до 1,5 мм. При расчете потерь напора в стальных трубах нефтепроводов и газопроводов значение эквивалентной шероховатости Трубопроводы разделяются на гидравлически гладкие и гидравлически шероховатые. Гидравлически гладкими называются трубопроводы, в которых отдельные струи потока, двигаясь параллельно друг другу, плавно обтекают все неровности внутренней поверхности трубы, в результате чего шероховатость не оказывает влияния на сопротивление потока. Такое явление наблюдается при ламинарном режиме. Коэффициент гидравлического сопротивления С увеличением турбулентности толщина пограничного слоя уменьшается, становится меньше естественной. Движущийся поток жидкости соприкасается с шероховатостью трубы, и потери напора по длине трубы увеличиваются. Получаются дополнительные завихрения, создаваемые выступами, за счет которых величина коэффициента гидравлического сопротивления увеличивается. В этом случае коэффициент сопротивления зависит от шероховатости стенок трубопровода и числа Рейнольдса (зона смешанного трения). При дальнейшем увеличении числа Рейнольдса повышается турбулентность потока и, начиная с определенного значения Рейнольдса, коэффициент Величина коэффициента гидравлического сопротивления при ламинарном режиме, когда Re < 2320, зависит только от числа Рейнольдса (от скорости) и не зависит от состояния стенок (шероховатости), определяется по формуле Пуазейля (француз, доктор медицины 1840 г.):
Для гидравлически гладких труб коэффициент
Для шероховатых труб коэффициент сопротивления зависит от относительной шероховатости
Для труб, по которым движутся нефтепродукты, величина При движении реальной жидкости кроме потерь напора на трение по длине потока могут возникать местные потери напора. В местных сопротивлениях изменяется скорость по величине (сужение, расширение), направлению (колено) или одновременно по величине и по направлению (тройник). При обтекании турбулентным потоком какой-либо преграды происходит отрыв транзитной струи от стенки с образованием вихревых зон. Вихревые зоны образуются вследствие трения транзитной струи с жидкостью, находящейся в мертвых зонах. Деформация потока и вращение жидкости в мертвых зонах происходит за счет энергии основного потока, что и вызывает потерю напора в местных сопротивлениях. По предложению немецкого ученого Вейсбаха (1806 – 1871 гг.) местные потери напора принято выражать в частях от скоростного напора, подсчитанного за местным сопротивлением
где Значения коэффициентов местных сопротивлений приводятся в справочной литературе, а величины некоторых из них приведены в таблице 7.1.
Таблица 7.1
|

 , диаметру d и кинематической вязкости
, диаметру d и кинематической вязкости  устанавливается безразмерный параметр Рейнольдса Re и характер движения жидкости. Затем определяют коэффициент гидравлического сопротивления
устанавливается безразмерный параметр Рейнольдса Re и характер движения жидкости. Затем определяют коэффициент гидравлического сопротивления  , потери напора h на трение в трубопроводе и гидравлический уклон i.
, потери напора h на трение в трубопроводе и гидравлический уклон i. , (7.1)
, (7.1) / s – это гидравлический радиус, равный отношению смоченного периметра
/ s – это гидравлический радиус, равный отношению смоченного периметра  к площади сечения s. Для трубы круглого сечения смоченный периметр равен
к площади сечения s. Для трубы круглого сечения смоченный периметр равен  ∙d, а площадь сечения
∙d, а площадь сечения  . Скоростной напор зависит от величины средней скорости
. Скоростной напор зависит от величины средней скорости  .
. , (7.2)
, (7.2) – средняя скорость движения жидкости, м/с; l – длина трубы, м; d – внутренний диаметр трубы, м; g = 9,81 м/с2 – ускорение свободного падения.
– средняя скорость движения жидкости, м/с; l – длина трубы, м; d – внутренний диаметр трубы, м; g = 9,81 м/с2 – ускорение свободного падения. , (7.3)
, (7.3) и подставив его в выражение 7.2, получим:
и подставив его в выражение 7.2, получим: . (7.4)
. (7.4) (7.5)
(7.5) равна 0,5 – 0,7 от максимальной величины естественной шероховатости.
равна 0,5 – 0,7 от максимальной величины естественной шероховатости.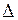 берут равным 0,1 – 0,2 мм.
берут равным 0,1 – 0,2 мм. . (7.6)
. (7.6) . (7.7)
. (7.7) . (7.8)
. (7.8) лежит в пределах 0,01 – 0,03. Для приближенных расчетов величину
лежит в пределах 0,01 – 0,03. Для приближенных расчетов величину  , (7.9)
, (7.9) – безразмерный коэффициент или коэффициент местного сопротивления зависит от формы последнего.
– безразмерный коэффициент или коэффициент местного сопротивления зависит от формы последнего.


