Понятие определенного интеграла
Пусть функция f(x) определена на отрезке [a,b]. Разделим отрезок на n произвольных частей точками а = х0 < x1< x2 <… < xn = b. Выберем на каждом элементарном отрезке произвольную точку xk. Длину каждого отрезка обозначим Dхk. Длину наибольшего из отрезков обозначим через d. Составим сумму всех произведений f (xk)Dхk . При различных разбиениях отрезка [а,b] на части будут получаться различные суммы, которые называются интегральными суммами. Определенныминтегралом от функции f(x) на отрезке [a,b] называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков d стремится к нулю: I =
Другими словами, из всей совокупности неопределенного интеграла F(х) + С можно выбрать один – определенный интеграл, если будут заданы пределы изменения для переменной х от a до b. Определенный интеграл обозначается символом:
где а – нижний предел интегрирования; b – верхний предел интегрирования.
Процесс вычисления определенного интеграла производится по формуле Ньютона - Лейбница:
Чтобы вычислить определенный интеграл нужно: 1.найти неопределенный интеграл от функции, в котором постоянная С = 0; 2. в полученном выражении подставить вместо х сначала верхний предел b, затем вычесть выражение с нижним пределом а. Формула Ньютона –Лейбница устанавливает связь определенного интеграла с неопределенным интегралом.
|

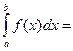


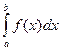 ,
,


