Основные свойства определенного интеграла
Постоянный множитель C можно выносить за знак определенного интеграла. Определенный интеграл от суммы (разности) непрерывных функций равен сумме (разности) определенных интегралов.
Приложение определенного интеграла И его геометрический смысл Площадь фигуры, ограниченной кривой y = f(x), осью Ох и двумя вертикальными прямыми х = а и х = b (а < b), вычисляется по формуле: S = В этом заключается геометрический смысл определенного интеграла, то есть данный определенный интеграл численно равен площади указанной криволинейной трапеции. Если фигура ограничена графиком непрерывной и неположительной на отрезке [a,b ] функции f(x), осью Ох и прямыми х = а, х = b, то площадь криволинейной трапеции вычисляется по формуле: S = - Пример Дано: y = х, у = 0, пределы интегрирования: а = 0, b = 4 Решение Фигура представляет собой прямоугольный треугольник с катетами равными 4 ед.
Замена переменной в определенном интеграле
где х = ф(t) – функция непрерывная вместе со своей производной на отрезке a £ t £b. При замене переменной в определенном интеграле необходимо заменить пределы интегрирования таким образом: a = ф (a) и b = ф (b).
|
= 
+ 
= 
= 
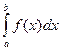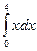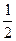(42 – 0) = 8.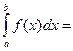
ф¢(t)dt,
