Однородные дифференциальные уравнения 1-го порядка.
Определение 1. Уравнение 1-го порядка Пример 1. Показать, что функция Решение.
Что и требовалось доказать. Теорема. Любая функция Определение 2. Уравнение В котором M И N – однородные функции одной и той же степени, т. е. обладают свойством Очевидно, что это уравнение всегда может быть приведено к виду Однородное уравнение приводится к уравнению с разделяющимися переменными с помощью замены искомой функции Y по формуле Y=Zx, Где Z(X) – новая искомая функция. Выполнив эту подстановку в уравнении (4.2), получим: Интегрируя, получаем общий интеграл уравнения относительно функции Z(X)
Замечание. Иногда целесообразно вместо указанной выше подстановки использовать подстановку X=Zy.
|
называется однородным, если для его правой части при любых 
справедливо соотношение 
, называемое условием однородности функции двух переменных нулевого измерения.
- однородная нулевого измерения.
,
- однородна и, наоборот, любая однородная функция 
нулевого измерения приводится к виду 
.
(4.1)
при всех 
, называется однородным.
(4.2), хотя для его решения можно этого и не делать.
или 
или 
.
, который после повторной замены 
дает общий интеграл исходного уравнения. Кроме того, если 
- корни уравнения 
, то функции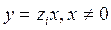 
- решения однородного заданного уравнения. Если же 
, то уравнение (4.2) принимает вид
и становится уравнением с разделяющимися переменными. Его решениями являются полупрямые: 
.
