Линейные дифференциальные уравнения 1-го порядка.
Линейным уравнением 1-го порядка называется уравнение, линейное относительно искомой функции и ее производной. Оно имеет вид:
Где P(X) И Q(X) – заданные непрерывные функции от X. Если функция И называется линейным однородным уравнением, в противном случае Линейное однородное дифференциальное уравнение (7.2) является уравнением с разделяющимися переменными:
Выражение (7.3) есть общее решение уравнения (7.2). Чтобы найти общее решение уравнения (7.1), в котором функция P(X) обозначает ту же функцию, что и в уравнении (7.2), применим прием, называемый методом вариации произвольной постоянной и состоящий в следующем: постараемся подобрать функцию С=С(X) Так, чтобы общее решение линейного однородного уравнения (7.2) являлось бы решением неоднородного линейного уравнения (7.1). Тогда для производной функции (7.3) получим:
Подставляя найденную производную в уравнение (7.1), будем иметь:
Или Откуда Первое слагаемое в этой формуле представляет общее решение (7.3) линейного однородного дифференциального уравнения (7.2), а второе слагаемое формулы (7.4) есть частное решение линейного неоднородного уравнения (7.1), полученное из общего (7.4) при Теорема. Если известно одно частное решение линейного неоднородного дифференциального уравнения Однако надо отметить, что для решения линейного неоднородного дифференциального уравнения 1-го порядка (7.1) чаще применяется другой метод, иногда называемый методом Бернулли. Будем искать решение уравнения (7.1) в виде Объединим, например, второе и третье слагаемые последнего выражения и вынесем функцию U(X) за скобку: Потребуем обращения в нуль круглой скобки: Решим это уравнение, полагая произвольную постоянную C равной нулю: Решая его, получим: Следовательно, общее решение уравнения (7.1) имеет вид:
Заключение (итог занятия): (повторение основных положений лекции, обобщение изложенного, установление связей изложенного с последующим материалом). Оснащение занятия: Ä доска, Ä раздаточный материал - учебно-методическое пособие "Дифференциальные уравнения" Домашнее задание: Ä Математика: учеб. пособие §2.2. Ä Расчётно-графическая работа по теме «Применение дифференциальных уравнений первого порядка для решения задач»
Литература: Основные источники:
Дополнительные источники:
|

 , (7.1)
, (7.1)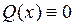 , То уравнение (7.1) имеет вид:
, То уравнение (7.1) имеет вид:  (7.2)
(7.2)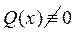 оно называется линейным неоднородным уравнением.
оно называется линейным неоднородным уравнением.
 (7.3)
(7.3) .
.
 .
. , где
, где  - произвольная постоянная. В результате общее решение неоднородного линейного уравнения (7.1) будет
- произвольная постоянная. В результате общее решение неоднородного линейного уравнения (7.1) будет  (7.4)
(7.4) 
 . Этот важный вывод выделим в виде теоремы.
. Этот важный вывод выделим в виде теоремы. , то все остальные решения имеют вид
, то все остальные решения имеют вид  , где
, где  - общее решение соответствующего линейного однородного дифференциального уравнения.
- общее решение соответствующего линейного однородного дифференциального уравнения. . Тогда
. Тогда  . Подставим найденную производную в исходное уравнение:
. Подставим найденную производную в исходное уравнение:  .
.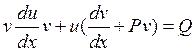 (7.5)
(7.5) .
. . С найденной функцией V(X) вернемся в уравнение (7.5):
. С найденной функцией V(X) вернемся в уравнение (7.5):  .
. .
. .
.


