Электрический заряд. Электрическое поле в вакууме. Число силовых линий точечного заряда. Закон Кулона.

101. - волновые уравнения в однородной,

непроводящей среде

102. - уравнение плоской волны, бегущей в произвольном направлении

103. или - вектор Пойнтинга

104. или - импульс электромагнитной волны

Электрический заряд. Электрическое поле в вакууме. Число силовых линий точечного заряда. Закон Кулона.

Электрический заряд – св-ва элементарных частиц, из кот. состоит вещ-во. Это такое же св-во частиц как их масса, форма и т.д.

Особенности электрического заряда:

1) не может быть ‹ некоторой минимальной величины «е», названной элементарным зарядом.

2) заряд передается только порциями, кратными электрическому заряду

q=Ne, N =1,2,3 q- заряд

3) в электрически изолированной сис-ме полный заряд остается неизменным в любых процессах проходящих в этой сис-ме – закон сохранения заряда.

формула Кулона.

r – расстояние

– коэффициент пропорциональный

ε₀- эл. постоянная е_r – орт вектора F

закон Кулона для тел в вакууме

электрич. заряды взаимодействуют благодаря образованию вокруг них электрич. поля, кот. действует на любой пробный заряд.

существует 2 типа заряда:

положительный и отрицательный

одноименные заряды отталкиваются, а разноименные притягиваются.

эта сила является характеристикой пробного заряда так как не зависит от величины q_пр. Е – напряженность поля заряда q на r. Если поле создается несколькими зарядами, то результирующая поля – векторная сумма полей отдельных зарядов.

принцип суперпозиции эл.полей.

графически эл.поле изображается с помощью силовых линий тока (воображаемые линии, проводимые таким образом, что касательная в любой точке, показывает направление вектора E, а их густота величину вектора Е.)

G – густота линий

 

 

S – площадь сферы

N = количество линий пронизывающих поверхность

линии поля могут возникать только в заряде и уходить по заряду в бесконечность (положит. заряд), либо приходить по заряду из бесконечности и замыкаться в заряде (отрицат. заряд).

 

Поток вектора напряженности и электростатического поля. Закон Гаусса для электростатического поля в интегральной форме.

 

Дана жидкость, текущая по трубе.

 

- поток вектора скорости.

 

cosα - так как площадка находится под углом.

dS- дополнительный вектор.

если дано векторное поле а, то его поток через площадку dS:

если нормаль направлена по направлению вектора, то поток положит., а если против направления, то поток отрицат. → если поверхность замкнута, и пронизывается вектором α, то поток вектора α:

N₂- количество линий входящих в поверхность

N₁ - количество линий выходящих из поверхности

дан заряд q_1, окруженный производной замкнутой поверхностью S.

 

 

если имеем n- зарядов то полный заряд

теорема Гаусса в интегральной форме для электростатического поля.

 

 

Дивергенция вектора напряженности электростатического поля. Теорема Гаусса в дифференциальной форме.

Дано векторное поле вектора V в некоторой жидкости.

тогда внутри поверхности есть источник.

 

тогда внутри поверхности есть стоки.

Если внутри поверхности есть и источники, и стоки то

при V→0,

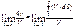
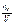отношение удельной мощности всех источников и стоков к объему поверхности.

суммарная мощность всех источников и стоков, заключенное в эл. V dV.

- суммарная мощность всех источников и стоков всего объема.

- теорема Остроградского- Гаусса.

- объемная плотность заряда

- дифференциальная форма теоремы Гаусса для вектора электрич. поля.