Пусть заданы векторы в прямоугольной системе координат
Пусть заданы векторы в прямоугольной системе координат
Скалярное произведение векторов. Определение. Скалярным произведением векторов
Свойства скалярного произведения: 1) ( 2) ( 3) ( 4) ( 5) (m Если рассматривать векторы
( Используя полученные равенства, получаем формулу для вычисления угла между векторами:
Формула для нахождения проекции вектора на вектор:
Векторное произведение векторов. Определение. Векторным произведением векторов 1) вектор 2) 3)
Обозначается:
j
Свойства векторного произведения векторов: 1) 2) 3)[ (m 4) [ 5) Если заданы векторы:
[
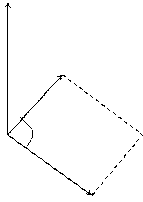
6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах
Смешанное произведение векторов. Определение. Смешанным произведением векторов Обозначается ( Смешанное произведение
Свойствасмешанного произведения:
1)Смешанное произведение равно нулю, если: а) хоть один из векторов равен нулю; б) два из векторов коллинеарны; в) векторы компланарны. 2) 3) 4) 5) Объем треугольной пирамиды, образованной векторами треугольной призмы 6)Если
7)Если
|

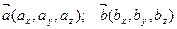 тогда линейные операции над ними в координатах имеют вид:
тогда линейные операции над ними в координатах имеют вид: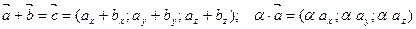
 и
и  называется число, равное произведению длин этих сторон на косинус угла между ними.
называется число, равное произведению длин этих сторон на косинус угла между ними. (
( ) = (
) = (
 ) =
) = 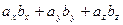



 , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям: , где j - угол между векторами
, где j - угол между векторами 
 или
или  .
.
 ;
;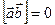 , если
, если  , то
, то

 по модулю равно объему параллелепипеда, построенного на векторах
по модулю равно объему параллелепипеда, построенного на векторах 




 ;
; , четырехугольной пирамиды
, четырехугольной пирамиды 
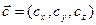 , то
, то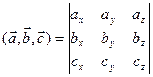
 >0, то векторы образуют правую тройку, если
>0, то векторы образуют правую тройку, если 


