СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

К понятию скалярного произведения приводит необходимость определения угла между векторами и их модулей. Эти метрические характеристики появляются в задаче вычисления работы, совершаемой заданной постоянной силой F при прямолинейном перемещении материальной точки на расстояние AB. Тогда работа определяется в виде А=|F|×|AB|cos(F^ÙAB).:

Линейное векторное пространство оснащенное скалярным произведением называется евклидовым.

Скалярным произведением (ск.пр) двух векторов называется число (скаляр) равное произведению их модулей на косинус угла между ними

a×b=|a|×|b|cos(a^Ùb)

Используя определение проекции вектора на ось, в качестве которой можно рассматривать любой из двух векторов можно представить ск.пр. следующим образом a×b=|a|×|b|cos(a^Ùb)=|a|×пр_ab=|b|×пр _ba

(а,b)=|a| |b| cos j, j <90, (а,b)>0; j=90, (а,b)=0; j>90, (а,b)<0.

Из определения с.к. векторов как произведения трех скаляров следует, что оно является скаляром и обладает свойствами:

1. Коммутативность: a×b=b×a;
2. Дистрибутивность: a×(b+c)=a×b+a×c;
3..Линейность: следует из свойства линейности операции проектирования c×(aa+bb)=|c|пр_c(aa+bb)=|c|(aпр_ca + bпр_cb) = a|c|пр_ca + b|c|пр_cb= aac + bbc;
4. Ассоциативность относительно скалярного множителя:l(a×b)=(la)×b=a×(lb)

(а,а)=|a|² – скалярный квадрат.

Определение: два вектора называются ортогoнальными, когда ск.пр.равно 0. Условие перпендикулярности a×b = 0 Û cosj = 0 Û a ^ b

Определение: вектор называется нормированным, если его скалярный квадрат равен 1.

Определение: ортом вектора а называется вектор ед. длины имеющий одинаковое направление с вектором а. e_a=a/|a|

Базисные вектора удовлетворяющие условию перпендикулярности образуют ортогональный базис, если кроме того они по длине единичны, то базис называют ортонормированным. Для такого базиса принято обозначение i - единичный вектор оси ОХ, j -оси ОУ, k -оси ОZ.

Существует понятие скалярного квадрата: a²= a×a=|a|² Þ |а| = - модуль вектора |a + b|² + |a-b|²=2|a|²+2|b|² - cумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

Теорема: Если векторы а и b заданы координатами в ортонормированном базисе, то их скалярное произведение равно сумме произведений соответствующих координат.

Найдем формулу угла между векторами по определению скалярного произведения. cos j=(a,b)/|a||b|=x₁x₂+y₁y₂+z₁z₂/(x₁²+y₁²+z₁²)^0,5×(x₂²+y₂²+z₂²)^0,5

a×b = |a|×|b|cosj, где j = (а^b) Þ в координатной форме a×b = a_xb_x+ a_yb_y+a_zb_z

В ортонормированном базисе можно использовать матричную запись скалярного произведения в виде произведения вектор строки на вектор столбец a×b = × = a_xb_x+ a_yb_y+a_zb_z

Тройка некомпланарных векторов a,b,c, начало которых совмещены, называется правой, если кратчайший поворот от вектора а к вектору b виден совершающимся против часовой стрелки из конца вектора с.

В противном случае тройка называется левой.

1. Если a,b,c -правая, то тройки b,c,a и c,a,b будут тоже правыми. Такая перестановка называется циклической перестановкой. Т.е. при циклической перестановке ориентация тройки не меняется.
2. Если a,b,c -правая, то тройки b,a.c и a,c,b -левые. Т.е., если поменять местами какие-нибудь два вектора, то ориентация тройки изменится. Векторным произведением a´b двух векторов a и b называется вектор, модуль и направление которого определяются следующим образом:
1) модуль вектора a´b равен произведению модулей векторов сомножителей на синус угла между ними: |a´b|=|a|×|b|sin(a^Ùb), т.е. площади параллелограмма, построенного на векторах сомножителях |a´b| = S _пар
2) направление вектора a´b перпендикулярно плоскости, содержащей вектора сомножители, и если смотреть из конца вектора a´b, то кратчайший поворот первого сомножителя ко второму виден и против часовой стрелки. тройка векторов a, b a´b -правая.

Из определения векторного произведения a´b следуют его свойства:

определения векторного произведения.

СВОЙСТВА векторного произведения:

1. a´b =0 <=>a||b.
2. Антикоммутативность:a´b =- b´a;
3. Дистрибутивность: a´ (b+c)= a´b + a´c или; (a+b)´c= a´c + b´c;
4..Билинейность(линейность по обеим аргументам):следует из свойства линейности операции проектирования c´(aa+bb) = a(a´c)+ b(b´c);
5. Ассоциативность относительно скалярного множителя: l(a´b) =(la)´b=a´(lb)

6. Теорема: Пусть векторы а и b заданы координатами в ортонормированном базисе, тогда векторное произведение равно определителю третьего порядка в первой строке которого наход–ся базисны векторы, во второй – координаты первого вектора, в третьей – координаты второго.

При использовании соотношения между базисными векторами i´j =k, j´i =-k j´k =i, k´j =-i, k´i =j,,i´k=-j. получим координатное выражение a´b=(а_х i+ a_y j+ а_z k) ´(b_х i+ b_y j+ b_z k)= = (а_Y b_Z - b_Y a_Z)i+ (а_Z b_X - b_Z a_X)j +(а_х b_y - b_х a_y)k.

Векторное произведение применяется для:

1) для определения направления перпендикулярного плоскости двух данных векторов;
2) для определения момента М относительно точки А силы F, приложенной к точке В М = АВ´F, при этом поворот плоскости содержащей вектор плечо АВ и силу F из конца вектора М виден против часовой стрелки;
3) Линейная скорость v при вращательном движении точки удаленной от центра вращения на радиус r равна векторному произведению угловой скорости w на радиус вектор r: v = w´r, причем |v| = |w||r| и из конца вектора угловой скорости w вращение происходит против часовой стрелки.

Смешанным произведением упорядоченной тройки векторов a, b, с называется число (скаляр) полученное при скалярном произведении третьего вектора с на вектор равный векторному произведению a´b двух других сомножителей поскольку последней операцией является скалярное произведение то результат смешанного произведения (a´b)×с -число (скаляр)

При перестановке каких либо двух соседних сомножителей в смешанном произведении оно меняет знак abс= -acb = bca = -bac= сab= - сba.

Для того,чтобы a,b,c были компланарными <=> abc=0.. Для того,чтобы a,b,c были линейно зависимыми <=> (abc)=0.

Трилинейность: (a+b)cd=acd+bcd

Вычисление смешанного произведения abс векторов a, b, с заданных своими координатами определяется как величина определителя третьего порядка, в 1-ой строке которого записаны координаты первого сомножителя векторов a, во 2-ой координаты b и в 3-ей координаты с,т.е. abс=

Используя представление cкалярного произведения через проекцию, имеем для смеш. пр. |abс|=|a´b |×|c|×|cos(a´b^c)| =|a´b|×|пр_a´bс|. Поскольку |a´b| = S_пар, и |пр_a´bс|=h_пар. высота параллелипепида, построенного на векторах a, b, с. Следовательно модуль смешанного произведения равен объему паралллелепипеда. построенного на векторах a, b, с |abс|=V_пар. Если abс= 0, то объем равен нулю и вектора a, b, с лежат в одной плоскости и их называют компланарными. Если abс>0, то вектора a, b, с образуют правую тройку, если abс<0 то вектора a, b, с образуют левую тройку. Смешанное произведение позволяет подсчитать не только объем параллелограмма V_пар но и объем треугольной пирамиды V_пир =¹/₆ V_пар, поскольку площадь треугольника в два раза меньше площади параллелогрмма и пирамида с той же высотой и основанием в три раза меньше объема параллелепипеда.

Если векторы a,b,c компланарны, то их смешанное произведение равно 0. Если векторы a,b,c не компланарны, то модуль.смешанного произведения равен объему параллелепипеда,построенного на этих векторах, причем смешанное произведение положительно,если тройка a,b,c - правая, и отрицательно,если тройка векторв -левая.

Задание1.

Даны координаты вершин пирамиды A ₁(x₁, y₁, z₁), A₂(x₂, y₂, z₂), A ₃(x₃; y₃; z₃); A₄(x₄, y₄, z₄). Найти: 1) длину ребра A₁A₂; 2) угол между ребрами A₁A₂ и A₁A ₄; 3) площадь грани A₁A₂A₃; 4) объем пирамиды.

1) Находим длину ребра как модуль вектора a=A₁A₂ с координатами a={x₂ - x₁, y₂ - y₁, z₂ - z₁}. Модуль вектора |a| =|A₁A₂|= .
2) Аналогично находим вектор с=A₁A₄ с координатами с={x₄ - x₁, y₄ - y₁, z₄ - z₁} и его модуль |b| = , затем, используя определение скалярного произведения a×с = |a|×|ñ|cosj, где j = (à^с), и представление скалярного произведения через координаты сомножителей a×с= [(x₂ - x₁) (x₄ - x₁)+(y₂ - y₁)(y₄ - y₁)+(z₂ - z₁)(z₄ - z₁)] и находим cos(A₁A₂^A₁A₄) = cosj =a×с/|a|×|с|.
3) Площадь грани A₁A₂A₃;находим как площадь треугольника построенного на векторах а и b=A₁A₃ с кординатами b={x₃ - x₁, y₃ - y₁, z₃ - z₁} равного половине площади параллелограмма S_D=¹/₂ S_пар= ¹/₂|a´b|. Находим векторное произведение a´b= = (à_Y b_Z - b_Y a_Z)i+ (à_Z b_X - b_Z a_X)j +(а_Х b_y - b_Х a_y)k. S_D= ¹/₂|a´b|.= ¹/₂ .
4) Находим объем треугольной пирамиды ребрами A₁A₂A₃A ₄. V_пир =¹/₆ V_пар =

=¹/₆ |abс|=¹/₆ mod .

Два вектора a={a₁,a₂,a₃} и b={b₁,b₂,b₃} равны тогда и только тогда, когда равны их соответствующие координаты в одном и том же базисе. Необходимым и достаточным условием коллинеарности векторов a={a₁,a₂,a₃} и b={b₁,b₂,b₃},b¹0, является пропорциональность их соответствующих координат: a₁=lb₁,a₂=lb₂,a₃=lb_3. Необходимым и достаточным условием компланарности трех векторов a={a₁,a₂,a₃}, b={b₁,b₂,b₃} и c={c₁,c₂,c₃} является равенство:

=0

Линейные операции над векторами сводятся к линейным операциям над координатами. Координаты суммы векторов a={a₁,a₂,a₃} и b={b₁,b₂,b₃} равны суммам соответствующих координат: a+b={a₁+b₁,a₂+b₂,a₃+b₃}. Координаты произведения вектора а на число l равны произведениям координат а на l:

lа= {lа₁,la₂, la₃}.

Скалярным произведением (а, b) ненулевых векторов а и b называют произведение их модулей на косинус угла j между ними:

(а, b) = | а |×| b | cosj.

За j принимается угол между векторами, не превосходящий p. Если а=0 или b=0, то скалярное произведение полагают равным нулю. Скалярное произведение обладает свойствами:

(a, b)= (b, а) (коммутативность),

(a, b+с)= (a,b) + (а,с) (дистрибутивность относительно сложения векторов),

l(a,b)=(la, b) =(a,lb) (сочетательность относительно умножения на число),

(a,b)=0, лишь если а=0 или (и) b=0 или a^b.

Для вычисления скалярных произведений векторов часто пользуются декартовыми прямоугольными координатами, т.е. координатами векторов в базисе, состоящем из единичных взаимно перпендикулярных векторов (ортов) i, j, k (ортонормированный базис). Скалярное произведение векторов:

a={a₁,a₂,a₃} и b={b₁,b₂,b₃}

заданных в ортонормированном базисе, вычисляется по формуле:

(a,b)=a₁b₁+a₂b₂+a₃b₃

Косинус угла j между ненулевыми векторами a={a₁,a₂,a₃} и b={b₁,b₂,b₃} может быть вычислен по формуле:

где и

Косинусы углов вектора a={a₁,a₂,a₃} с векторами базиса i, j, k называют. направляющими косинусами вектора а:

, , .

Направляющие косинусы обладают следующим свойством:

cos²a+cos²b+cos²g=1

Осью называется прямая с лежащим на ней единичным вектором е-ортом, задающим положительное направление на прямой. Проекцией Пр. _е а вектора a на ось называют направленный отрезок на оси, алгебраическое значение которого равно скалярному произведению вектора а на вектор е. Проекции обладают свойствами:

Пр. _е (a+b)= Пр. _е a+ Пр. _е b (аддитивность),

Пр. _е a = Пр. _е la (однородность).

Каждая координата вектора в ортонормированном базисе равна проекции этого вектора на ось, определяемую соответствующим вектором базиса.

В пространстве различают правые и левые тройки векторов. Тройка некомпланарных векторов а, b, с называется правой, если наблюдателю из их общего начала обход концов векторов a, b, с в указанном порядке кажется совершающимся по часовой стрелке. В противном случае a,b,c - левая тройка. Правая (левая) тройка векторов располагается так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки(см. рис). Все правые (или левые) тройки векторов называются одинаково ориентированными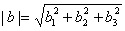.