Разложение вектора по ортам декартовой системы координат
Разложить по базису a, b вектор с, лежащий в плоскости базисных векторов значит представить его в виде c=xa + yb, где x, y - координаты вектора c в базисе a, b, аналогично для пространственного базиса. При решении задач координатным методом или с помощью векторов - главным является удачный выбор системы координат - желательно чтобы система координат естественным образом определялась условиями задачи
Система координат это начало координат О и направляющие векторы осей, длины которых определяют масштаб на осях. Для перпендикулярных и единичных по длине направляющих векторов принято обозначение i, j, k. На плоскости направляющие векторы осей (базис) - любая пара неколлинеарных (непараллельных) векторов, в пространстве базис - любая тройка некомпланарных (непараллельных одной плоскости) векторов.
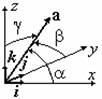
Коэффициенты этого разложения - координаты вектора в данной системе координат - проекции вектора на координатные оси, что можно записaть в виде a={ах, аy, аz} = ахi+ аyj+ аzk. Направляющие косинусы вектора - косинусы углов a = (i^а), b = (j^а), g = (k^а), которые вектор cоставляет с осями OХ, OY, OZ. (cosa = aх/|a|, cosb = ay/|а|, cosg = az/|a|, тогда ах= прoхa = |a|cosa, аy=прoya = |a|cosb, аz=прoza =|a|cosg, cos2a+ cos2b+ cos2g =1 Если возвести последние три равенства в квадрат и сложить, то получим основное тригонометрическое тождество для направляющих косинусов вектора: Пусть в декартовой системе кooрдинат в пространстве заданы две точки или два их радиуса вектора rA = ОА ={хA, yA, zA}, r B = OB ={хB, yB, zB}. Из векторного равенства АВ=rВ - rА = {хВ-хА, yВ-yА, zВ-zА}, т. е. для нахождения координат вектора при известных координатах его начала и конца следует из координат координат конца вычесть координаты начала соответственно a = {xВ - xА; yВ - yА; zВ - zА} МОДУЛЬ (ДЛИНА) ВЕКТОРА:- расстояние от начала до конца вектора. Модуль вектора с помощью его координат определяется:|a| = = В заданном базисе любой вектор линейного пространства однозначно определяется своими координатами Ecли два вектора равны, то равны их координаты, следовательно равны модули и направляющие косинусы Сложение векторов: координатной форме a ± b={àx ± bx; ay ± by; az ± bz}. Коллинеарность векторов a =lb, причем |a |=|l | b| - условие коллинеарности в координатной форме имеет вид: Иногда удобно представлять вектор не в виде строки составленной из его координат а в виде столбца a=
|

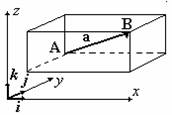
 Модуль вектора | АВ | =
Модуль вектора | АВ | = 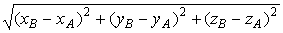 cовпадает с формулой расстояния между точками. А и В.
cовпадает с формулой расстояния между точками. А и В.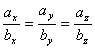 .
. и рассматривать его как матрицу размера 3´1. Такая запись векторов называется матричной.
и рассматривать его как матрицу размера 3´1. Такая запись векторов называется матричной.


