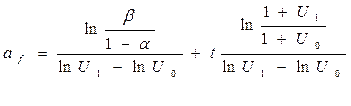значения Р заданное.

 

Пример: при принятии решения об отбраковки партии

продукции Р заданное- вероятность того что в

партии содержится некоторая доля

бракованных изделий, которая допустима (это

допустимый % брака). Нужно на основе

конечной выборки объема определить, что %

брака реальный < заданного, т.е. P<Pзад.

Результаты наблюдений на каждом шаге эксперимента обозначим через , где

ì 1, если проверенные изделия не бракованные

í

î 0, если проверенные изделия бракованные

n - число проверок или опытов

среди них m проверок- число случаев, когда

изделия бракованные.

В данной задаче неизвестный параметр , который есть вероятность того, что партия изделий не бракованная, т.е. определяется условие, что P<Pзад.

Следующий шаг: определение допустимых границ, в которых может находиться Pзад., т.е. определяет интервал P <Pзад.<P , в котором текущие результаты являются безразличными и требуют проведения эксперимента. Тогда

и .

Будем считать, что результаты эксперимента можно описать биноминальной функцией распределения:

где N-объем генеральной совокупности

n- объем выборки

P- вероятность того, что имеет место в 1-ом

эксперименте наличие требуемого признака

{в нашем случае вероятность появления

неисправных изделий}.

Вероятность

n - количество экспериментов

m - брак с вероятностью P

n - количество экспериментов

m - брак с вероятностью P

Далее - критерий

Вальда.

Для каждого значения n вычисляется значение функции

и проверяется выполнение одного из трех условий:

- принимаем гипотезу.

- не принимаем гипотезу.

- проводим новый эксперимент.

Можно преобразовать приведенные выражения к следующему виду, к виду который содержит в данной форме:

, причем

Если , то переходим к следующему эксперименту.

 

 

m

 

N

 

 

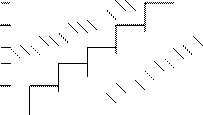
Как только ступенчатая функция вышла за пределы, то мы принимаем решение.

 

Сравнительная оценка двух систем.

 

Задача возникает при сравнении эффективности двух тактических приемов военных действий или при сравнении 2-х технических систем, имеющих одинаковые функциональные назначения.

Математическая постановка: на основе 2-х серий испытаний по комплексам:

требуется проверить гипотезу, что .

a – показатели, характеризующие 1-ую систему.

b – показатели для 2-ой системы.

В частности можно определить или 1.

Если 1- успешный эксперимент, 0- неуспешный эксперимент.

Тоже для b.

В данном последовательном критерии рассматриваются пары , которые принимают значения

01 –1 испытание

11 –2 испытание

00 –3 испытание

10 –4 испытание

Относительное превосходство 2-го процесса над 1-м измеряется отношением их показателей эффективности, которые могут быть представлены:

где Р1 и Р2- вероятность того, что успешно или не успешно прошло испытание. Они не известны.

Если U=1-процессы одинаковы.

U>1-P2 эффективней P1.

U<1- P1 предпочтительнее P2.

Для принятия решения для сравнительной оценки процесса выбираем 2 значения U0 и U1, при чем U0<U1 такие, что отказ процесса или системы 1 в пользу системы 2 рассматривается как ошибка, имеющая практическое значение.

Т.е. U<U0-ошибка 1-го рода

U>U1-ошибка 2-го рода

Используя эти соотношения можно аналогично предыдущему примеру показать, что принятие решения определяется по числу результатов эксперимента.

t=t1+t2

Если a - испытания продолжаются

- принимаем процесс 1

- принимаем процесс 2

 

 

Практическая часть

 

 

Цель работы: Ознакомиться с методами последовательного анализа в задачах подготовки и проведении испытаний.

 

2. Подготовить исходные данные для примера об отбраковки партии продукции.

Для первой этого вычислить заданные параметры:

- P0=0, 0№;

- Р1=3*Р0;

- a=0,02+Р0;

- b=(0,8*a; 1, 1*a; 1,4*a);

- (параметры биномиального распределения: р=10*Р0; n=1-число испытаний)

Составить последовательность случайных чисел (50)с биномиальны законом распределения которые в дальше интерпретируются как результаты испытаний. 0 – интерпретируется как неудачное испытание; 1 – удачное.

4 Построить, по приведенным в теории формулам, границы области принятия решения и используя таблицу случайных чисел определить число испытаний, на основе которого, принимается решение о завершении испытаний и выбранное решение при 3-х значениях b.

- Ознакомиться с методикой сравнительной оценки двух систем и привести описание методики организации процесса подготовки и проведения испытаний по этой методике.

- Построить статистическую модель хода испытаний в виде 2-х выборок из 50 двоичных значений (1– удачное испытание; 0 – неудачное испытание) полученных с помощью генерации биномиальных случайных чисел. Одна выборка – система А: р=0,(№+1), n =1; Вторая выборка – система Б: р=0,(№), n=1.

- Построить, по приведенным в теории формулам, границы области принятия решения и используя таблицу случайных чисел определить число испытаний, на основе которого, принимается решение о завершении испытаний и выбранное решение (т.е. предпочтение между системами А и Б) при α и 3-х значениях b взятых из пункта 2.

4. Вычислить по полученной статистике классическим методом долю брака (Пункт 1) и предпочтительность систем (Пункт 3). Сравнить результаты с результатами полученными по методу Вальда.