Исследование функций автокорреляции случайных процессов. Пример: при принятии решения об отбраковки партии
Исследование функций автокорреляции случайных процессов
1. Цели работы: Исследование автокорреляционных функций стационарных случайных процессов, изучение методов аппаратурного корреляционного анализа стационарных случайных процессов. 2. Некоторые сведения из теории случайных процессов: Функцией автокорреляции случайного процесса
где
В случае стационарного процесса Автокорреляционная функция (АКФ) стационарного случайного процесса обладает следующими основными свойствами: 1. Автокорреляционная функция является чётной функцией переменной 2. Максимальное значение функции автокорреляции достигается при АКФ является характеристикой скорости изменения (ширины спектра) случайного процесса. Широкополосный (быстроменяющийся) процесс имеет быстро уменьшающуюся АКФ, тогда как АКФ медленно меняющегося процесса также уменьшается медленно. Мерой быстродействия, скорости изменения случайного процесса служит время корреляции Одним из таких критериев может быть, например, уменьшение значения АКФ в два раза по сравнению со значением её при Вторым критерием может быть ширина основания прямоугольника, высота которого равна дисперсии процесса, а площадь равна площади фигуры, ограниченной осями координат и кривой функции корреляции
В инженерной практике часто используется нормированная функция корреляции (коэффициент корреляции), представляющая собой отношение:
Тогда
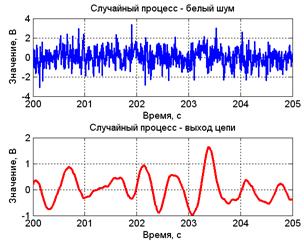
Рассмотрим функцию корреляции процесса, полученного в результате прохождения белого шума – процесса с постоянной спектральной плотностью мощности Функцию корреляции такого процесса Первый способ – использование частотного метода. В этом случае ищется спектральная плотность мощности процесса
Затем использованием обратного преобразования Винера-Хинчина находится функция корреляции:
Основным недостатком этого метода является иногда возникающая трудность вычисления интеграла в (5). Вторым методом является временной, использующий для записи выходного процесса интеграл свёртки:
где
Функция корреляции процесса
где учтено, что При использовании временного метода необходимо получить выражение для импульсной реакции цепи и вычислить интеграл типа свёртки (7) с учётом основного свойства импульсной реакции физически реализуемой цепи Рассмотрим функции корреляции процессов на выходах трёх цепей, используемых в настоящей лабораторной работе, при действии на входе белого шума со спектральной плотностью мощности
Рисунок 2 – Принципиальные схемы цепей, формирующих случайные процессы
Выражения для коэффициентов передачи и импульсных реакций указанных цепей имеют вид:
где
где
где
где В равенстве (13) предполагается, что потери энергии в цепи, схема которой представлена на рисунке 2, в. невелики и выполняется неравенство Применением временного метода можно получить следующие выражения для нормированных функций корреляции процессов Нормированная функция корреляции процесса
Нормированная функция корреляции процесса
Нормированная функция корреляции процесса
3. Характеристика лабораторной установки: Лабораторная работа выполняется с использованием пакета Simulink системы моделирования MATLAB. В основу построения модели лабораторной установки положен принцип замены вычисления среднего по множеству усреднением по времени, справедливый для стационарных случайных процессов, обладающих эргодическим свойством [1-3]. Упрощённая схема лабораторной установки представлена на рисунке 3, а блок-схема её модели – на рисунке 4.
Рисунок 3 – Упрощённая структурная схема лабораторной установки
Генератор шума (ГШ) формирует случайный широкополосный процесс, математической моделью которого является белый шум – случайный процесс с постоянной спектральной плотностью мощности. Подключая с помощью перемычек исследуемые цепи, можно сформировать описанные выше процессы
где
В связи с тем, что на выходе перемножителя возможно присутствие постоянной составляющей напряжения, наличие которой эквивалентно наличию математического ожидания в процессе
где
Структурная схема Simulink-модели, соответствующая реальной установке, изображённой на рисунке 4, приведена на рисунке 3. Здесь гауссов белый шум с генератора Gaussian Noise Generator или равномерный белый шум с генератора Uniform Noise Generator сразу подаётся на входы всех трёх исследуемых цепей, а к коррелометру (блок Correlometer) выходы цепей подключаются через управляемый переключатель (блок Multiport Switch). Время задержки
Рисунок 4 – Блок-схема модели для исследования статистических характеристик эргодических случайных процессов
Индикация результатов моделирования тройная: три сигнала – шум n (t), выход цепи X i(t) и траектория вычисления уровня корреляции R x(t, tau) – передаются в рабочее пространство для последующего построения временных зависимостей, на осциллографе Scope4 можно наблюдать два последних процесса, и, наконец, на цифровом дисплее в конце времени моделирования можно получить числовую оценку уровня корреляции
4. Лабораторное задание: 4.1. В нижнем левом углу программу MATLAB нажмите кнопу старт и выберите Simulink => Library Browser. Создайте рабочее поле File => NEW => Model. Находя в библиотеке необходимые элементы (!!!используйте при необходимости поиск!!!) перетаскивайте их на созданную рабочую область. Настройте параметры, для получения 4.2. Для проведения эксперимента, необходимо собрать схему из типовых элементов, используя при этом браузер библиотеки Simulink, рис.4. Провести измерения, необходимые для построения автокорреляционной функции 4.3 Провести аналогичные измерения и построения функций автокорреляции 4.4 Подключить ко входу цепей генератор равномерного белого шума и повторить измерения функций автокорреляции
5. Требования к отчёту: Отчёт должен содержать: 1) формулировку целей и задач лабораторной работы; 2) функциональную схему установки с подключёнными приборами регистрации; 3) таблицы и графики экспериментальных исследований (пример на рисунке 4); 4) Вывод по результатам эксперимента: как автокорреляционная функция зависит от спектральной плотности мощности случайного сигнала. 5) Ответы на контрольные вопросы
6. Контрольные вопросы: 6.1. Дать определения функции корреляции, функции ковариации, коэффициента корреляции. Указать различия между приведёнными понятиями. 6.2. Записать выражения для функции корреляции с усреднением по множеству значений и с усреднением по времени. Указать, при каких условиях результаты усреднения по множеству значений и по времени одинаковы.
при моделировании RLC -цепи
6.3. Какой может быть функциональная схема коррелометра при использовании метода усреднения по множеству реализаций? 6.4. Разработать функциональную схему коррелометра с использованием усреднения по времени, построенного на базе ЭЦВМ. 6.5. На вход линейной цепи поступает стационарный случайный процесс с известной функцией корреляции. Указать метод расчёта функции корреляции выходного процесса в стационарном режиме при известном комплексном коэффициенте передачи цепи. 6.6. Дать определение стационарного случайного процесса в узком и широком смысле. 6.7. Что такое эргодическое свойство стационарного случайного процесса? Привести пример стационарного процесса, не обладающего эргодическим свойством. 6.8. Дать определение спектральной плотности мощности стационарного случайного процесса. Какими свойствами обладает спектральная плотность мощности? 6.9. Разработать функциональную схему аппаратурного метода исследования спектральной плотности мощности (анализатора спектральной плотности мощности). 6.10. Указать связь спектральной плотности мощности с функцией корреляции случайного процесса. 6.11. Перечислить основные свойства автокорреляционной функции стационарного случайного процесса, обладающего эргодическим свойством. 6.12. Дать определение времени корреляции стационарного случайного процесса. Разработать функциональную схему экспериментального измерения времени корреляции случайного процесса.
|

 называется смешанный центральный момент второго порядка системы двух сечений
называется смешанный центральный момент второго порядка системы двух сечений  ,
,  , рассматриваемый как функция моментов времени
, рассматриваемый как функция моментов времени  и
и  :
: (1)
(1) – плотность вероятности системы
– плотность вероятности системы  ,
,  ;
; ,
,  – математические ожидания сечений
– математические ожидания сечений 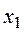 ,
,  – значения сечений
– значения сечений  и
и  соответственно.
соответственно. функция автокорреляции не зависит от значений моментов
функция автокорреляции не зависит от значений моментов  и
и  , а зависит от расстояния между ними
, а зависит от расстояния между ними  .
. .
. и равно дисперсии случайного процесса
и равно дисперсии случайного процесса  .
. , которое характеризует ширину АКФ по определённому критерию.
, которое характеризует ширину АКФ по определённому критерию. .
.
 (2)
(2) (3)
(3)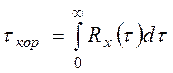 .
. – через линейную цепь с постоянными параметрами, которая характеризуется комплексным коэффициентом передачи
– через линейную цепь с постоянными параметрами, которая характеризуется комплексным коэффициентом передачи  .
. можно найти двумя способами [1-3].
можно найти двумя способами [1-3]. :
: . (4)
. (4) (5)
(5) (6)
(6) – входной процесс, являющийся белым шумом со спектральной плотностью
– входной процесс, являющийся белым шумом со спектральной плотностью  ;
; – импульсная реакция рассматриваемой цепи.
– импульсная реакция рассматриваемой цепи. может быть найдена из выражения
может быть найдена из выражения (7)
(7) – функция корреляции белого шума.
– функция корреляции белого шума. при
при  . При вычислении интеграла в равенстве (7) при
. При вычислении интеграла в равенстве (7) при  можно непосредственно интегрировать по приведённой формуле. Для отрицательных значений
можно непосредственно интегрировать по приведённой формуле. Для отрицательных значений  можно использовать свойство чётности функции автокорреляции
можно использовать свойство чётности функции автокорреляции  и дополнительного интегрирования не проводить.
и дополнительного интегрирования не проводить. . Принципиальные схемы этих цепей приведены на рис. 2. а, 2. б, 2. в.
. Принципиальные схемы этих цепей приведены на рис. 2. а, 2. б, 2. в.
 ,
, 
 (8)
(8) – постоянная времени цепи (рис. 2. а),
– постоянная времени цепи (рис. 2. а), ,
,  (9)
(9) (10)
(10) – постоянная времени звена двухзвенной RC-цепи (рис. 2. б)
– постоянная времени звена двухзвенной RC-цепи (рис. 2. б) ,
,  , (12)
, (12) ,
,  ,
, (13)
(13) .
. .
. ,
,  и
и  на выходах приведённых на рисунке 2 схем электрических цепей, если на их входах действует белый шум:
на выходах приведённых на рисунке 2 схем электрических цепей, если на их входах действует белый шум: :
: (14)
(14) :
: (15)
(15) :
: (16)
(16)
 ,
,  и
и  ,
,  (17)
(17) – напряжение на выходе коррелометра при подаче на вход процесса
– напряжение на выходе коррелометра при подаче на вход процесса  ,
, – время усреднения, в первом приближении равное величине, обратной полосе ФНЧ,
– время усреднения, в первом приближении равное величине, обратной полосе ФНЧ, – время задержки, установленное положением переключателей цепи задержки,
– время задержки, установленное положением переключателей цепи задержки, – постоянный коэффициент, значение которого определяется значениями коэффициентов передачи усилителей и схемы перемножителя.
– постоянный коэффициент, значение которого определяется значениями коэффициентов передачи усилителей и схемы перемножителя. , то вычисление значений нормированной функции корреляции в момент задержки
, то вычисление значений нормированной функции корреляции в момент задержки  целесообразно выполнять по формуле:
целесообразно выполнять по формуле: (18)
(18) – напряжение на выходе коррелометра при конкретном значении
– напряжение на выходе коррелометра при конкретном значении  ,
, – напряжение на выходе коррелометра при максимальной задержке
– напряжение на выходе коррелометра при максимальной задержке  ,
, – напряжение на выходе коррелометра при
– напряжение на выходе коррелометра при  .
. задаётся как единственный параметр коррелометра и меняется от 0 до 10* RC мкс. Поскольку постоянная времени RC = 1 с, то в модели максимальная задержка
задаётся как единственный параметр коррелометра и меняется от 0 до 10* RC мкс. Поскольку постоянная времени RC = 1 с, то в модели максимальная задержка  практически для всех цепей лежит за пределами времени корреляции каждого из процессов.
практически для всех цепей лежит за пределами времени корреляции каждого из процессов.
 , путём подачи на входы цепей гауссова белого шума. Проанализировать и зарисовать графики временных зависимостей, спектрограммы и гистограммы процессов на входе и выходе RC -цепи.
, путём подачи на входы цепей гауссова белого шума. Проанализировать и зарисовать графики временных зависимостей, спектрограммы и гистограммы процессов на входе и выходе RC -цепи. и
и  для процессов на выходах второй и третьей цепей. Для этого с помощью блока N cepi задать номер цепи в переключателе Multiport Switch. Построить все корреляционные функции
для процессов на выходах второй и третьей цепей. Для этого с помощью блока N cepi задать номер цепи в переключателе Multiport Switch. Построить все корреляционные функции  ,
,