Темы. Парето оптимальные распределения и их представление в ящике Эджворта. Равновесие в экономике обмена. Закон Вальраса. Экономика Робинзона Крузо
На 15 полно оплачиваемых детей – предоставляется 1 бесплатный руководитель.
Ремарка: Данные цены, указанные в пунктах 1), 2) и 3), (нетные) в евро за 1 чел. в день включают в себя: размещение, питание, страховку, туристический налог, НДС и бесплатное использование спортивных сооружений в комплексе (тенис-корт, игровые поля в дневное время суток), 24-часовая охрана комплекса, медицинское обслуживание на територии комплекса, спасатели на пляже, зонтики на пляже и зонтики и лежаки у бассейна - бесплатно.
ГУ-ВШЭ, 2007-2008 уч.г. Микроэкономика, модуль-1
Домашнее задание №1
ДЗ сдается преподавателю, ведущему семинары не позже 17-20 октября 2007 г. Темы. Парето оптимальные распределения и их представление в ящике Эджворта. Равновесие в экономике обмена. Закон Вальраса. Экономика Робинзона Крузо
Решение: Ошибка заключается во фразе «вынужден ограничить свое потребление этой величиной». Смысл равновесных цен и равновесия вообще – в том, что в этой ситуации каждый участник обмена сможет купить и продать ровно столько каждого товара, сколько захочет. Нетрудно заметить, что при ценах
Решение: Во-первых, известно, что функции избыточного спроса обладают однородностью степени «0» по ценам. Проверим, соблюдается ли это свойство для заданных нам функций:
Как видим, обе функции однородны степени «0». Во-вторых, если предпочтения монотонны, функции избыточного спроса удовлетворяют закону Вальраса: стоимость совокупного избыточного спроса на все товары тождественно (то есть, для всех возможных наборов цен) равна нулю. Иными словами, Нетрудно видеть, что это выражение равно нулю не для всех возможных цен, а только для p1 = p2. Следовательно, либо предпочтения немонотонны, либо предлагаемые функции не являются функциями избыточного спроса.
Решение: Рассмотрим последовательно три класса точек – над диагональю ящика Эджворта, под диагональю, и на диагонали. Вначале рассмотрим произвольно взятую точку z1 над диагональю ящика, через которую проходят кривые безразличия UA и UB (см. Рисунок 1). Для потребителя A, точке z1 предпочитаются любые наборы, лежащие выше кривой безразличия UA (в области, заштрихованной синим, не включая саму кривую безразличия). Для потребителя B, точке z1 предпочитаются любые наборы, лежащие (в его системе координат) выше кривой безразличия UB (в области, заштрихованной красным, не включая саму кривую безразличия). Таким образом, любой набор внутри треугольной области, где красная и синяя штриховки пересекаются, одновременно принесет обоим потребителям большую полезность, чем z1, т.е. будет Парето-улучшением для z1. Следовательно, никакая произвольно взятая точка z1, лежащая выше диагонали ящика Эджворта, Парето-оптимальной не является. Аналогичным образом можно показать, что никакая произвольно взятая точка z2, лежащая ниже диагонали ящика Эджворта, также не является Парето-оптимальной.
Рисунок 1.
Теперь рассмотрим произвольную точку z3, лежащую на диагонали ящика Эджворта (Рисунок 2). Как и раньше, для А наборы, более предпочтительные чем z3, лежат в области, заштрихованной синим (не включая саму кривую безразличия UA), а для B – в области, заштрихованной красным (не включая саму кривую безразличия U’B). Однако теперь эти области не пересекаются – не существует таких наборов, которые были бы лучше, чем z3 для одного потребителя, и по крайней мере не хуже – для другого. Таким образом, любые точки на диагонали ящика Эджворта не могут быть улучшены по Парето, и являются Парето-оптимальными. Множество всех Парето-оптимальных распределений – диагональ ящика.
Рисунок 2.
б) Изобразите кривые цена-потребление и найдите равновесие/равновесия (укажите цены и соответствующие распределения). Решение: Найдем кривую цена-потребление для потребителя A. Для этого последовательно рассмотрим его бюджетное ограничение при всех возможных комбинациях цен, и для каждой их комбинации (для каждого угла наклона бюджетного ограничения) ответим на вопрос: какие из доступных потребителю А наборов будут лежать на самой высокой кривой безразличия? На самом деле, возможно всего три принципиальных случая (см. Рисунок 3). Случай 1: px = 0. Бюджетное ограничение BC1 является горизонтальной линией, проходящей через точку первоначального запаса ω. Самой высокой из достижимых кривых безразличия здесь является U1A; следовательно, потребитель А может выбрать любой набор, одновременно принадлежащий U1A и BC1 (на «горизонтальном луче» U1A) Случай 2: px > 0, py > 0. Бюджетное ограничение BC2 является наклонной линией, проходящей через точку первоначального запаса ω. Самой высокой из достижимых кривых безразличия здесь является U2A, а единственным набором, одновременно принадлежащим U2A и BC2 - набор z, лежащий на диагонали ящика. Случай 3: py = 0. Бюджетное ограничение BC3 является вертикальной линией, проходящей через точку первоначального запаса ω. Самой высокой из достижимых кривых безразличия здесь является U3A; следовательно, потребитель А может выбрать любой набор, одновременно принадлежащий U3A и BC3 (на «вертикальном луче» U3A).
Рисунок 3
Объединяя на одном графике точки потребительского выбора А при всех комбинациях цен, мы получаем следующую кривую «цена-потребление» (Рисунок 4):
Рисунок 4
Аналогично, найдем кривую цена-потребление для потребителя B, также рассмотрев его бюджетное ограничение при всех возможных комбинациях положительных цен. Здесь возможно пять принципиальных случаев (см. Рисунок 5): Случай 1: px < py. Угол наклона бюджетного ограничения BC1 меньше, чем угол наклона кривых безразличия. Самой высокой из достижимых кривых безразличия является U1B; единственный набор, одновременно принадлежащий U1B и BC1 - набор z1, лежащий на оси 0BXB. Случай 2: px = py. Бюджетное ограничение BC2 фактически совпадает с кривой безразличия U2B, она же является самой высокой из доступных; потребитель может выбрать любую точку на кривой безразличия U2B. Случай 3: px > py. Угол наклона бюджетного ограничения BC3 больше, чем угол наклона кривых безразличия. Самой высокой из достижимых кривых безразличия является U2B; единственный набор, одновременно принадлежащий U2B и BC3 - набор ω – первоначальный запас. Остается рассмотреть два специальных случая: когда цены x и y равны нулю. Поскольку полезность потребителя B монотонно возрастает по обоим благам, ясно, что если какое-то из них бесплатно, потребитель захочет иметь его бесконечно много. Соответственно, при px = 0 выбираемый набор будет находиться в бесконечности на оси 0BXB, при py = 0 - в бесконечности на оси 0YB.
Рисунок 5 Объединяя на одном графике точки потребительского выбора B при всех комбинациях цен, мы получаем следующую кривую «цена-потребление» (Рисунок 6). Ясное дело, точки в бесконечности мы нарисовать не сможем.
Рисунок 6 Наконец, объединяя кривые «цена-потребление» для А и B на одном графике, мы видим, что они пересекаются в двух точках – Z и ω (Рисунок 7). Для того, чтобы точка пересечения кривых «цена-потребление» была равновесием, оба потребителя должны стремиться попасть в эту точку при одних и тех же ценах. Мы видим, что для Z это условие справедливо – при px = py оба потребителя захотят переместиться именно в нее (точнее, А захочет, а B будет не против). Однако, в точку ω потребитель А захочет попасть только при px = 0, а при таких ценах потребитель B будет стремиться оказаться совсем в другом месте – в бесконечно удаленной точке на оси 0BXB.
Рисунок 7 Равновесное распределение можно найти как решение системы двух уравнений в координатах потребителя А:
Соответственно, равновесие:
в) Как изменятся ваши ответы на пункты (а) и (б), если первоначальные запасы имеют вид:
Решение: Множество Парето-оптимальных распределений будет представлять собой отрезок 0AZ’. Ответ на пункт (б) изменится следующим образом (см. Рисунок 8):
Рисунок 8 (По-хорошему, это нужно было бы тоже обосновать!) Точками пересечения кривых «цена-потребление» будут Z’ и ω. В точку ω потребитель А захочет попасть только при px = 0, а при таких ценах потребитель B будет стремиться оказаться в бесконечно удаленной точке на оси 0BXB - ω не может быть равновесием. Однако точка Z’ может быть равновесием при
Рисунок 9. Отсюда также следует, что в равновесии цены обоих товаров не нулевые. В-третьих, ясно, что при ненулевых ценах все решения задачи потребителя А будут удовлетворять свойству: xA = 2yA (1)
Докажем от противного: пусть xA > 2yA – решение задачи потребителя А. Тогда UA = 2yA. Возьмем δ > 0 товара x, такую, что xA - δ > 2(yA + δ) и обменяем ее на Ясно, что равновесие будет лежать на пересечении двух линий – бюджетного ограничения, и луча xA = 2yA: Найдем угол наклона бюджетного ограничения:
Заметим, что общее бюджетное ограничение должно проходить через точку первоначальных запасов (рассмотрим ее в координатах потребителя А):
Выражая отсюда py, получим:
Подставив (3) в (2), получим уравнение:
Воспользуемся известными нам размерами ящика Эджворта, чтобы привести это уравнение к координатам потребителя А:
И наконец, подставим в выражение (4) необходимое условие максимизации полезности потребителя A (1):
Упростив это выражение, мы получим:
Уравнение (5) имеет два корня: yA = 7 и yA = 4. Первый корень мы отбрасываем, так как при нем оптимальное распределение не помещалось бы в ящике Эджворта (потребитель А должен был бы получать yA = 4; xA = 8; - из (1) xB = 5; yB = 5; - в силу монотонности предпочтений потребителей А и B и известных нам размеров ящика Эджворта. px/py = 1; - из (2)
Равновесие:
6. Пусть предпочтения Робинзона заданы функцией полезности а) Найдите Парето оптимальное распределение. б) Найдите равновесие. Будет ли равновесное распределение Парето оптимальным?
Решение: а) Парето-оптимальное состояние возникает при таком распределении Робинзоном своего свободного времени между трудом и отдыхом, которое приносит ему максимальную полезность:
Поскольку эта функция вогнута по l, необходимым и достаточным условием максимума будет:
Домножим на 3, и приведем дроби к одному знаменателю:
б) Поскольку мы уже знаем, что Парето-оптимальное распределение в этой экономике только одно, осталось доказать, что оно и будет равновесием. В силу Второй теоремы экономики благосостояния и того, что предпочтения Робинзона монотонны, это действительно так. Найдем равновесные цены из дифференциальной характеристики оптимума:
подставив с = 16 и l =16, мы получим, что равновесные цены:
|

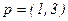 и распределение
и распределение  образуют равновесие в экономике обмена с двумя потребителями, функции полезности которых имеют вид
образуют равновесие в экономике обмена с двумя потребителями, функции полезности которых имеют вид  и
и  , а первоначальные запасы заданы векторами
, а первоначальные запасы заданы векторами  и
и  . Поскольку для потребителя А товары являются совершенными заменителями, то он будет тратить весь свой доход на более дешевый товар, то есть
. Поскольку для потребителя А товары являются совершенными заменителями, то он будет тратить весь свой доход на более дешевый товар, то есть 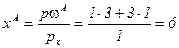 и
и  . Потребитель В ценит только второй товар и хотел бы весь свой доход потратить на него, но, осознавая, что в экономике имеется лишь 6 единиц второго товара, вынужден ограничить свое потребление этой величиной:
. Потребитель В ценит только второй товар и хотел бы весь свой доход потратить на него, но, осознавая, что в экономике имеется лишь 6 единиц второго товара, вынужден ограничить свое потребление этой величиной:  . В результате у него остается еще 2 единицы первого товара:
. В результате у него остается еще 2 единицы первого товара:  . Итак, мы показали, что выполнена рациональность потребителей и, кроме того, как мы видим, совокупное потребление по каждому благу в точности равно его запасу в экономике, то есть мы имеем дело с равновесием.
. Итак, мы показали, что выполнена рациональность потребителей и, кроме того, как мы видим, совокупное потребление по каждому благу в точности равно его запасу в экономике, то есть мы имеем дело с равновесием. единиц блага у. То, что он не сможет этого сделать (его партнер способен купить лишь 3 единицы х, и предложить к продаже лишь 1 единицу y), означает, что предлагаемое нам распределение не является равновесным.
единиц блага у. То, что он не сможет этого сделать (его партнер способен купить лишь 3 единицы х, и предложить к продаже лишь 1 единицу y), означает, что предлагаемое нам распределение не является равновесным. . Могут ли следующие функции
. Могут ли следующие функции  и
и  являться функциями избыточного спроса для этой экономики?
являться функциями избыточного спроса для этой экономики?
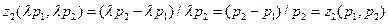
 . Подставив предлагаемые нам функции избыточного спроса в это тождество, мы получим:
. Подставив предлагаемые нам функции избыточного спроса в это тождество, мы получим: 
 и
и  , соответственно. Вектора первоначальных запасов имеют вид:
, соответственно. Вектора первоначальных запасов имеют вид:  и
и  .
. 








 .
.
 (при безупречном решении здесь стоило нарисовать бюджетное ограничение для этого случая, кривые безразличия, и показать, почему оба потребителя захотят оказаться именно в точке Z’). Итак, новое равновесие:
(при безупречном решении здесь стоило нарисовать бюджетное ограничение для этого случая, кривые безразличия, и показать, почему оба потребителя захотят оказаться именно в точке Z’). Итак, новое равновесие: .
. и
и  , соответственно. Вектора первоначальных запасов имеют вид:
, соответственно. Вектора первоначальных запасов имеют вид:  и
и  .
. 
 товара y. Полезность составит UA = 2(yA + δ) – новый набор доступен и лучше старого – первоначальный набор не был решением задачи потребителя А.
товара y. Полезность составит UA = 2(yA + δ) – новый набор доступен и лучше старого – первоначальный набор не был решением задачи потребителя А. Если px = 1, то:
Если px = 1, то: (2)
(2)
 (3)
(3)
 (4)
(4)
 ; (5)
; (5)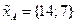 ). Таким образом:
). Таким образом:
 , где
, где  -количество потребляемых кокосов, а
-количество потребляемых кокосов, а  – свободное время. Предположим, что Робинзон открыл фирму по производству кокосов. Кокосы можно достать только собственным трудом, причем технология фирмы описывается производственной функцией вида
– свободное время. Предположим, что Робинзон открыл фирму по производству кокосов. Кокосы можно достать только собственным трудом, причем технология фирмы описывается производственной функцией вида  . Робинзон может работать максимум 24 часа в сутки.
. Робинзон может работать максимум 24 часа в сутки.