Методы математического описания и структурные схемы САР
Теория автоматического регулирования сформировала единый подход к анализу и синтезу систем различной физической природы (систем механических, электрических, гидравлических, акустических и т.д.) Основан он на математическом описании основных элементов САР, включающем и сами объекты регулирования. При этом математическое описание САР представляется в виде уравнения, левая часть которого включает в себя члены, описывающие внутренние (собственные) свойства элементов, управляемые сигналы и их производные. Правая часть уравнений содержит управляющие и внешние воздействия и их производные.
где
Математическое описание движения объектов управления и регуляторов составляется на основе физических законов, определяющих протекающие процессы. Уровень сложности этого описания может быть совершенно различным. Так, например, электрическая цепь, представленная на рисунке 1.3,а и газотурбинный двигатель на рисунке 1.3,б могут быть описаны одинаковыми дифференциальными управлениями:
Таким образом, выражения (1.1) и (1.2) показывают, что изменение выходного напряжения электрической цепи R-C и газотурбинного двигателя описываются одинаковыми дифференциальными уравнениями первого порядка, отличающимися только входящими в них коэффициентами. На практике уравнения, описывающие поведение объектов управления и регуляторов, бывают гораздо более сложными. Определение параметров движения реальных объектов даже с использованием современных ЭВМ представляет значительные трудности. Поэтому проектирование, расчеты параметров и обеспечение заданного качества работы САР основывается на определенных методах, которые заключаются в следующем. 1. Сложные объекты управления и регуляторы разбивают на отдельные типовые элементы, которые описываются достаточно простыми математическими уравнениями. Решения этих уравнений, а значит и свойства этих элементов известны заранее. Результатом этого разбиения являются структурные схемы объектов управления и регуляторов, которые показывают как отдельные элементы, образующие сложную систему, связаны между собой. 2. Для сравнительного анализа поведения отдельных элементов и устройств в целом используют стандартные возмущения в виде ступенчатой функции или гармонической функции (рисунок 1.4).
Рисунок 1.4 – Типовые возмущения используемые в теории автоматического регулирования и их аналитические выражения Реакция элемента или системы в целом на ступенчатое возмущение является функцией времени и называется переходным процессом. Реакция элемента или системы в целом на гармонические возмущения является функцией частоты и амплитуды возмущения и называется частотной характеристикой элемента или системы. Структурные системы САР в наглядной форме отображают состав систем и связи между ними. С их помощью удобно проводить расчеты САР методами анализа и синтеза. В связи с появлением современного программного обеспечения в автоматике используются унифицированные методы изображения элементов структурных схем, значительно упрощающие методы расчета систем на ЭВМ. Основные обозначения элементов структурные схем, используемые в приложении Simulink к MatLab (математическая лаборатория) представлены в таблице 1.1. Таблица 1.1 – Основные обозначения элементов структурных схем
В поле прямоугольника, обозначающего элемент системы, вписывают математическое описание свойств этого элемента, позволяющее определить взаимосвязь в изменении выходного сигнала Хвых в зависимости от изменения входного. Обычно такую взаимосвязь записывают в виде дифференциальных уравнений в полных или частных производных. В теории автоматического регулирования пользуются не уравнениями объектов и устройств систем регулирования, а их передаточными функциями. Под передаточной функцией понимается отношение изображений по Лапласу выходной величины объекта и устройства к изображению функции входной величины, полученных при нулевых начальных условиях. Передаточная функция обозначается Так, например, передаточная функция газотурбинного двигателя имеет общее выражение:
Структурная схема для исследования характеристик двигателя описываемого данной передаточной функцией имеет вид представленный на рисунке 1.5.
Рисунок 1.5 – Структурная схема изучения динамических характеристик двигателя
|

 ,
, - оператор, описывающий внутренние свойства САР или отдельного элемента;
- оператор, описывающий внутренние свойства САР или отдельного элемента; - оператор внешних управляющих воздействий на систему или отдельный элемент.
- оператор внешних управляющих воздействий на систему или отдельный элемент. - для электрической цепи; (1.1)
- для электрической цепи; (1.1) - для газотурбинного двигателя. (1.2)
- для газотурбинного двигателя. (1.2)













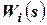 , где s – оператор дифференцирования
, где s – оператор дифференцирования  .
.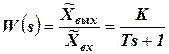 .
.



