АНАЛИЗ ДАННЫХ
Элементы информации о каждом объекте, которые мы собираем в процессе исследования, называются данными, и, как только они получены, перед нами начинает маячить конец работы. Наша цель на этом этапе – уяснить, что именно мы получили для решения проблемы исследования. Имеется ли какая-либо связь между поведением, которое мы надеемся объяснить или лучше понять, с одной стороны, и факторами, которые, как мы думаем, помогут нам сделать это, – с другой? Предположим, например, что, по нашим расчетам, люди, различающиеся уровнем образования, будут систематически различаться по степени вероятности участия в голосовании. Во многих случаях это можно сделать, ответив на три вопроса. Наш первый вопрос: так ли это? Действительно ли люди, отличающиеся друг от друга по одной из этих переменных, будут последовательно различаться и по другой? Будут ли более образованные люди последовательно отличаться от менее [c.34] образованных большей или меньшей склонностью принимать участие в голосовании? Анализируя полученные данные, мы могли бы, например, выяснить, что менее образованные люд и принимают участие в голосовании почти столь же часто, как и более образованные, что знание уровня образования не дает возможности ни предсказать, ни объяснить, почему вероятность участия в голосовании для данного человека отличается от вероятности участия для кого-то другого. Если это так, то мы заявляем, что уровень образования не оказывает влияния на вероятность голосования или, иначе говоря, что между этими двумя переменными нет никакой связи. Таким образом, анализ не подтверждает наши ожидания. С другой стороны, если мы обнаружим, что в шести или семи случаях из десяти знание уровня образования позволяет точно предсказать, примет ли данный человек участие в голосовании, мы получим данные в поддержку нашего утверждения о связи этих двух переменных. Следовательно, мы выясняем, что, когда речь идет о голосовании, более образованные люди систематически отличаются от менее образованных, и получаем возможность понять поведение при голосовании объектов нашего исследования. Итак, основное, что необходимо выяснить при оценке гипотезы, – это наличие между двумя переменными статистической зависимости. Как только эта связь установлена, необходимо задать не менее важный вопрос: как связаны эти две переменные? Будут ли более образованные люди участвовать в голосовании с большей вероятностью, чем менее образованные? Или же связь между этими переменными носит еще более сложный характер? Если мы продумали нашу гипотезу и в результате можно предполагать, что уровень образования связан с голосованием, мы, вероятно, имеем в виду одну из этих возможностей.
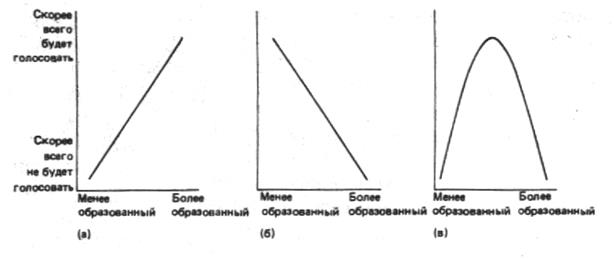
Рис. 1.1. Соотношение между уровнем образования и вероятностью голосования Например, можно было бы утверждать, что при наличии более высокого уровня образования возрастает вероятность наличия у человека навыков и знаний, необходимых для того, чтобы поддерживать у него интерес к политике. Соответственно, более образованный человек скорее примет участие в голосовании, чем тот, кто обладает меньшими навыками или располагает меньшей информацией. Таким образом, мы вправе ожидать, что участие в голосовании будет более [c.35] частым или более типичным для тех исследуемых нами людей, чей уровень образования выше. Этот тип соотношения иллюстрируется на рис.1.1а (точки на прямой представляют соответствующие значения переменных). Однако мы могли бы также считать, что, чем образованнее становится человек, тем сильнее он разочаровывается в политической деятельности. В соответствии с этой точкой зрения образованность ведет к разочарованию, что в свою очередь уменьшает желание принимать участие в голосовании. В этом случае мы можем ожидать, что чаще голосовать будут менее образованные из обследуемых нами людей. Этот тип соотношения иллюстрируется на рис.1.1б. Наконец, мы могли бы даже утверждать, что образование лишь до определенной степени увеличивает возможности для занятий политикой и интерес к ней, тогда как люди с более высоким уровнем образования (например, обучающиеся в колледже) гораздо сильнее разочарованы в политике и потеряли к ней интерес. В этом случае мы можем ожидать, что наиболее часто будут голосовать люди, имеющие средний уровень образования, в то время как на полюсах степень участия в голосовании будет ниже. Это более сложное соотношение иллюстрируется на рис.1.1в. В каждом из случаев между уровнем образования человека и вероятностью его участия в голосовании имеется определенная зависимость, однако совершенно очевидно, что следствия, вытекающие из этих разных соотношений, совершенно различны. Таким образом, мы можем [c.36] обнаружить сильную взаимозависимость между двумя переменными и тем не менее оказаться не в состоянии подтвердить свою гипотезу. Нужно задать себе и третий, возможно, менее очевидный вопрос. Насколько вероятно, что то или иное соотношение, обнаруженное нами при исследовании небольшого числа объектов, будет также получено при исследовании всей той совокупности, из которой выбирались эти объекты? Если угодно, это сформулированный в статистической форме вопрос о том, насколько обоснованно наше утверждение, что небольшая выборка репрезентативна, или типична, для генеральной совокупности. Если, выбирая для исследования конкретные объекты, мы принимали правильные решения, можно с уверенностью утверждать, что наши выводы, хотя и основаны на нескольких объектах, применимы ко всем объектам без исключения. Если мы ошибались, степень нашей уверенности может быть теперь не столь высокой. К сожалению, как станет яснее из последующих глав, когда выводы основаны на выборке из совокупности, никогда нельзя доверять им полностью. [c.37]
|