Колебания.
Колебательный контур состоит из катушки индуктивностью Дано: Найти: Решение: Число колебаний, совершаемых за время уменьшения амплитуды силы тока в
где
R – сопротивление резистора. Подставим эти выражения в (1), получим:
Отсюда искомое сопротивление:
Подставим числовые значения и произведем вычисления:
Ответ: Варианты индивидуальных заданий.
5.1. Записать уравнение гармонических колебаний при следующих параметрах: 1) А = 10 см, 2) А = 5,0 см, 3) А = 4,0 см,
5.2. Материальная точка совершает гармонические колебания по закону
5.3. Определить смещение от положения равновесия материальной точки, совершающей гармонические колебания при: 1) t1 = 0; 2) t2 =
5.4. Написать уравнение гармонического колебания, если амплитуда ускорения am = 50 см/с2, частота колебаний
5.5. Написать уравнение гармонического колебания, если амплитуда скорости υm = 63 см/с, период колебаний Т = 1 с, смещение точки от положения равновесия в начальный момент времени равно нулю. Найти амплитуду ускорения, частоту колебаний.
5.6. Точка совершает гармонические колебания. В некоторый момент времени смещение точки x = 5 см, скорость
5.7. Точка совершает гармонические колебания. Период колебания Т = 2 с, амплитуда А = 50 мм, начальная фаза
5.8. Материальная точка совершает колебание по закону синуса. Наибольшее смещение точки А = 20 см, наибольшая скорость
5.9. Начальная фаза колебаний точки
5.10. Материальная точка совершает колебания по закону x = 2
5.11. Дифференциальное уравнение гармонических колебаний имеет вид:
5.12. Амплитуда скорости материальной точки, совершающей гармоническое колебание, υm = 8 см/c, а амплитуда ускорения am = 16 см/с2. Найти амплитуду смещения и циклическую частоту колебаний.
5.13. Период колебаний математического маятника Т = 10 с. Длина этого маятника равна сумме длин двух других математических маятников, один из которых имеет частоту колебаний ν = 1/6 Гц. Чему равен период колебаний второго из этих маятников?
5.14. Два математических маятника имеют одинаковую массу, длины, отличающиеся в 1,5 раза, и колеблются с одинаковой угловой амплитудой. Какой маятник обладает большей энергией и во сколько раз?
5.15. Два математических маятника, длины которых отличаются на ∆l = 16 см, совершают за одно и тоже время один
5.16. За сколько времени маятник отклонится от положения равновесия на половину амплитуды, если период колебаний Т = 3,6 с?
5.17. Маятник совершает гармонические колебания. Через сколько времени он при первом колебании отклонится от положения равновесия на расстояние, равное
5.18. При фазе
5.19. Математический маятник длиной l = 2,5 м совершает колебания с амплитудой А = 10 см. Написать уравнение движения x = x(t).
5.20. Физический маятник представляет собой тонкий стержень, подвешенный за один из его концов. При какой длине стержня период этого маятника будет равен Т = 1 с?
5.21. Тонкий однородный стержень длиной l = 60 см может свободно вращаться вокруг горизонтальной оси, отстоящей на расстоянии x = 15 см от его середины. Определите период стержня, если он совершает малые колебания.
5.22. Однородный шарик подвешен на нить, длина которой равна радиусу шарика. Во сколько раз период малых колебаний этого маятника больше периода малых колебаний математического маятника с таким же расстоянием от точки подвеса до центра тяжести?
5.23. Однородный диск радиусом R = 20 см колеблется около горизонтальной оси, проходящей на расстоянии l = 15 см от центра диска. Определить период колебания диска относительно этой оси.
5.24. Тонкий обруч радиусом R = 50 см подвешен на вбитый в стену гвоздь и колеблется в плоскости, параллельной стене. Определите период колебания обруча.
5.25. Медный шарик, подвешенный к пружине, совершает вертикальные колебания. Как изменится период колебаний, если к пружине подвесить вместо медного шарика алюминиевый такого же радиуса?
5.26. Тонкий обруч, подвешенный на гвоздь, вбитый горизонтально в стену, колеблется в плоскости параллельно стене. Радиус обруча R = 30 см. Вычислить период колебаний Т обруча.
5.27. Кольцо радиусом R = 0,61 м и весом Р = 35 Н подвешено на горизонтальном гвозде: а) какова будет частота колебания кольца при его малых отклонениях от положения равновесия? б) какова длина эквивалентного математического маятника?
5.28. Найти период колебаний стержня длиной l = 0,5 м, который совершает малые колебания в вертикальной плоскости около горизонтальной оси, проходящей через точку, находящуюся на расстоянии d = 10 см от его верхнего конца.
5.29. Однородный диск радиусом R = 0,4 м колеблется в вертикальной плоскости около горизонтальной оси. Ось перпендикулярна диску и проходит через его край. Как изменится период колебаний диска, если ось перенести к центру параллельно самой себе на расстоянии
5.30. Диск радиусом R = 24 см колеблется около горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Определить частоту колебаний
5.31. Начальная фаза колебаний точки
5.32. Спиральная пружина под действием подвешенного к ней груза растянулась на ∆x = 6,5 см. Если груз оттянуть вниз, а затем отпустить, то он начнёт колебаться вдоль вертикальной линии. Определить период колебаний груза.
5.33. Груз массой m = 200 г подвешен к пружине с коэффициентом упругости k = 10 Н/м. Найти длину математического маятника, имеющего такой же период колебаний, как данный пружинный маятник.
5.34. Математический маятник массой m = 100 г и длиной
5.35. Висящий на пружине груз массой m = 0,10 кг совершает вертикальные колебания. Определить период гармонических колебаний груза, если для упругого удлинения пружины на ∆x = 1,0 см требуется сила F = 0,10 Н. Весом пружины пренебречь.
5.36. Под действием груза массой m = 200 г пружина растягивается на ∆x = 1,86 см. Грузу сообщили кинетическую энергию Е = 0,02 Дж, и он стал совершать гармонические колебания. Определить частоту и амплитуду колебаний.
5.37. Груз, подвешенный к спиральной пружине, колеблется по вертикали с амплитудой А = 8 см. Определите жесткость пружины k, если известно, что максимальная кинетическая энергия груза составляет Е = 0,8 Дж.
5.38. Груз, подвешенный к спиральной пружине, колеблется по вертикали с амплитудой А = 6 см. Определите полную энергию груза, если жесткость пружины k = 500 Н/м.
5.39. Спиральная пружина обладает жесткостью k = 25 Н/м. Тело какой массы должно быть подвешено к пружине, чтобы за t = 1 мин совершилось 25 колебаний?
5.40. Груз массой m = 0,3 кг, подвешенный к пружине, растягивает её на
5.41. К пружине подвешен груз m = 10 кг. Зная, что пружина под влиянием силы F = 9,8 Н растягивается на
5.42. Материальная точка массой m = 7,1 г совершает гармоническое колебание с амплитудой А = 2 см и частотой
5.43. Уравнение колебаний материальной точки массой m =16 г имеет вид:
5.44. Тело массой m = 5 кг совершает гармонические колебания с амплитудой А = 4 см. Найти период колебаний, если максимальная кинетическая энергия колеблющегося тела Ек.макс = 0,98 Дж.
5.45. Материальная точка массой m = 5 г колеблется согласно уравнению
5.46. Полня энергия тела массой m = 1 кг, совершающего гармонические колебания, Е = 1 Дж, максимальная возвращающая сила, действующая на тело, равна Fмакс = 10 Н. Написать дифференциальное уравнение колебаний и его решение, если начальная фаза
5.47. Материальная точка массой m = 10 г колеблется по закону x = 0,05sin(0,6t+0,8), м. Найти максимальную силу, действующую на точку, и полную энергию колеблющейся точки.
5.48. Тело массой m = 10 г совершает гармонические колебания по закону
5.49. Материальная точка массой m = 50 г совершает гармонические колебания согласно уравнению
5.50. Материальная точка массой m = 20 г совершает гармонические колебания по закону
5.51. Полная энергия гармонического колебания точки Е = 10 мкДж, а максимальная сила равна F = 0,5 мН. Напишите уравнение движения этой точки, если период колебаний Т = 4 с, а начальная фаза
5.52. Определите отношение кинетической энергии точки, совершающей гармонические колебания, к её потенциальной энергии, если известна фаза колебания.
5.53. Собственная частота колебаний некоторой системы составляет
5.54. Определить резонансную частоту колебательной системы, если собственная частота колебаний
5.55. Период затухающих колебаний Т = 1 с, логарифмический декремент затухания
5.56. Амплитуда затухающих колебаний маятника за t = 2 мин уменьшилась в 2 раза. Определить коэффициент затухания
5.57. Логарифмический декремент затухания колебаний маятника
5.58. Амплитуда затухающих колебаний математического маятника за t = 1 мин уменьшилась в 3 раза. Во сколько раз она уменьшится за t = 4 мин?
5.59. Начальная амплитуда затухающих колебаний маятника А0 = 3 см. По истечении t1 = 10 с – А1 = 1 см. Через сколько времени амплитуда колебаний станет равной А2 = 0,3 см?
5.60. За время, в течение которого система совершает N = 50 полных колебаний, амплитуда уменьшается в 2 раза. Определите добротность Q системы.
5.61. Частота свободных колебаний некоторой системы
5.62. Тело массой m = 100 г, совершая затухающие колебания, за
5.63. За
5.64. Логарифмический декремент затухания
5.65. Логарифмический декремент затухания
5.66. Через
5.67. Амплитуда колебаний маятника уменьшается в 10 раз за 100 полных колебаний. Определить логарифмический декремент затухания. Через сколько колебаний амплитуда маятника уменьшилась в e раз?
5.68. Колебательный контур состоит из катушки индуктивностью L = 10 мГн, конденсатора емкостью С = 0,1 мкФ и резистора с сопротивлением R = 20 Ом. Через сколько полных колебаний амплитуда тока в контуре уменьшится в e раз?
5.69. Определите логарифмический декремент затухания, при котором энергия колебательного контура за N = 5 полных колебаний уменьшается в n = 8 раз.
5.70. Колебательный контур содержит катушку индуктивностью L = 6 мкГн, конденсатор емкостью С = 10 нФ и резистор сопротивлением R = 10 Ом. Определите для случая максимума тока отношение энергии магнитного поля катушки к энергии электрического поля.
5.71. Частота затухающих колебаний в колебательном контуре с добротностью Q = 2500 равна
5.72. Гиря массой m = 0,5 кг, подвешенная на спиральной пружине жесткостью k = 50 Н/м, совершает колебания в вязкой среде с коэффициентом сопротивления r = 0,5 кг/с. На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону F = 0,1сos
5.73. Гиря массой m = 400 г, подвешенная на спиральной пружине жесткостью k = 40 Н/м, опущена в масло. Коэффициент сопротивления r для этой системы составляет 0,5 кг/с. На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону F = сos
5.74. Гиря массой m = 20 г, подвешенная на спиральной пружине жесткостью k = 50 Н/м, совершает колебания в вязкой среде с коэффициентом сопротивления r = 0,2 кг/с. На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону F = 0,2сos
5.75. Груз массой m = 2,5 кг, подвешенный к пружине с коэффициентом жесткости k = 3,6·102Н/м, совершает вынужденные колебания под действием внешней силы
5.76. Груз массой m = 0,1 кг подвешен на пружине с коэффициентом жесткости k = 10 Н/м. На груз действует вынуждающая сила, описываемая уравнением F = 2cos8t, Н. Коэффициент затухания
5.77. Вынужденные колебания описываются дифференциальным уравнением:
5.78. Два одинаково направленных колебания заданы уравнениями:
5.79. Точка участвует одновременно в двух гармонических колебаниях одинаковой частоты, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями
5.80. При сложении двух одинаково направленных гармонических колебаний с одной и той же частотой и амплитудами, равными А1 = 2 см и А2 = 4 см, получается гармоническое колебание с амплитудой А = 5 см. Найти разность фаз складываемых колебаний.
5.81. Два одинаково направленных гармонических колебания с одинаковой частотой и амплитудами А1 = 3 см и А2 = 5 см складываются в одно гармоническое колебание с амплитудой А = 7 см. Найти разность фаз складываемых колебаний.
5.82. Два одинаково направленных гармонических колебания одинакового периода с амплитудами А1 = 4 см и А2 = 8 см имеют разность фаз
5.83. Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями
5.84. Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями
5.85. Амплитуда результирующего колебания, получающегося при сложении двух одинаково направленных гармонических колебаний одинаковой частоты, обладающих разностью фаз
5.86. Разность фаз двух одинаково направленных гармонических колебаний одинакового периода Т = 4 с и одинаковой амплитуды А = 5 см составляет
5.87. Складываются два гармонических колебания одного направления, описываемых уравнениями
5.88. Колебательный контур содержит соленоид (длина l =5 см, площадь поперечного сечения S1 = 1,5 см2, число витков N = 500) и плоский конденсатор (расстояние между обкладками d = 1,5 мм, площадь пластинок S2 = 100 см2). Определите частоту собственных колебаний контура.
5.89. Колебательный контур состоит из катушки индуктивностью L = 0,1 Гн и конденсатора емкостью С = 39,5 мкФ. Заряд конденсатора q = 3 мкКл. Пренебрегая сопротивлением контура, запишите уравнение: 1) изменения силы тока в цепи в зависимости от времени; 2) изменения напряжения в зависимости от времени.
5.90. Сила тока в колебательном контуре, содержащем катушку индуктивностью L = 0,1 Гн и конденсатор, со временем изменяется согласно уравнению
5.91. Напряжение на обкладках конденсатора в колебательном контуре изменяется по закону U = 10cos104t, В. Емкость конденсатора С = 10 мкФ. Найти индуктивность контура и закон изменения силы тока в нём.
5.92. Сила тока в колебательном контуре изменяется по закону I = 0,1sin103t, А. Индуктивность контура L = 0,1 Гн. Найти закон изменения напряжения на конденсаторе и его емкость.
5.93. В колебательном контуре максимальная сила тока
5.94. Конденсатору емкостью С = 0,4 мкФ сообщается заряд q = 10 мкКл, после чего он замыкается на катушку с индуктивностью L = 1 мГн. Чему равна максимальная сила тока в катушке?
5.95. Максимальная сила тока в колебательном контуре
5.96. Энергия свободных затухающих колебаний, происходящих в колебательном контуре, составляет Е = 0,2 мДж, при медленном раздвигании пластин конденсатора частота увеличилась в 2 раза. Определить работу, совершённую против сил электрического поля.
5.97. Колебательный контур содержит катушку с общим числом витков N = 100, индуктивность L = 10 мкГн и конденсатор емкостью С = 1 нФ. Максимальное напряжение на обкладках конденсатора составляет U = 100 В. Определить максимальный магнитный поток, пронизывающий катушку.
5.98. Катушка без сердечника длиной l = 50 см и сечением S1 = 3 см2 имеет 1000 витков и соединена параллельно с конденсатором. Площадь пластин конденсатора S2 =75 см2. Расстояние между пластинами d = 5 мм, диэлектрик – воздух. Определить период колебаний Т контура.
5.99. Определить энергию электрического и магнитного полей колебательного контура в момент, когда энергия магнитного поля составляет 0,1 энергии электрического поля, если максимальный заряд конденсатора равен q = 10-8 Кл, а максимальное напряжение на его обкладках U = 440 В.
5.100. Колебательный контур имеет собственную частоту Колебания. Ι. Механические.
|

 , резистора и конденсатора емкостью
, резистора и конденсатора емкостью 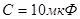 . Определить сопротивление резистора, если известно, что амплитуда тока в контуре уменьшается в
. Определить сопротивление резистора, если известно, что амплитуда тока в контуре уменьшается в  раз за 16 полных колебаний.
раз за 16 полных колебаний. ,
,  ,
,  .
.
 , (1)
, (1) - время релаксации,
- время релаксации,  ;
; - период затухающих колебаний,
- период затухающих колебаний, - собственная циклическая частота колебаний,
- собственная циклическая частота колебаний, - коэффициент затухания,
- коэффициент затухания,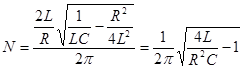 .
.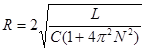
 .
.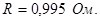
 рад,
рад,  = 2
= 2 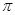 рад/сек;
рад/сек; рад, Т = 2,0 сек;
рад, Т = 2,0 сек; рад,
рад,  = 2,0 сек-1.
= 2,0 сек-1. , см. Определить амплитуду колебания А, начальную фазу
, см. Определить амплитуду колебания А, начальную фазу 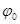 , период колебаний Т.
, период колебаний Т.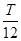 ; 3) t3 =
; 3) t3 =  ; 4) t4 =
; 4) t4 =  . Начальная фаза колебаний
. Начальная фаза колебаний  , амплитуда колебаний А.
, амплитуда колебаний А. = 20 см/с и ускорение a = - 80 см/с. Найти циклическую частоту и период колебаний в рассматриваемый момент времени.
= 20 см/с и ускорение a = - 80 см/с. Найти циклическую частоту и период колебаний в рассматриваемый момент времени. . Найти скорость точки в момент времени, когда смещение от положения равновесия x = 2,5 см.
. Найти скорость точки в момент времени, когда смещение от положения равновесия x = 2,5 см.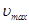 = 40 см/с. Написать уравнение колебаний и найти максимальное ускорение точки.
= 40 см/с. Написать уравнение колебаний и найти максимальное ускорение точки. 15о. Через сколько времени от начала движения смещение точки первый раз достигает величины равной половине амплитуды? Период колебаний Т = 12 с.
15о. Через сколько времени от начала движения смещение точки первый раз достигает величины равной половине амплитуды? Период колебаний Т = 12 с. , см. Найти амплитуду, период, частоту, начальную фазу колебаний, а также максимальные значения скорости и ускорения.
, см. Найти амплитуду, период, частоту, начальную фазу колебаний, а также максимальные значения скорости и ускорения. . Найти период и частоту этих колебаний.
. Найти период и частоту этих колебаний. амплитуды, если период колебаний Т = 4 с, начальная фаза
амплитуды, если период колебаний Т = 4 с, начальная фаза  ?
? рад смещение х = 1см. Найти амплитуду колебаний и смещение при фазе
рад смещение х = 1см. Найти амплитуду колебаний и смещение при фазе 
 рад.
рад. радиуса от прежнего положения.
радиуса от прежнего положения.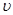 такого физического маятника.
такого физического маятника. равна нулю, период колебаний Т = 1 с. Определить ближайшие моменты времени, в которые смещение, скорость и ускорение вдвое меньше амплитудных значений.
равна нулю, период колебаний Т = 1 с. Определить ближайшие моменты времени, в которые смещение, скорость и ускорение вдвое меньше амплитудных значений. = 1 м совершает гармонические колебания по закону x = 2,5sin2
= 1 м совершает гармонические колебания по закону x = 2,5sin2  x = 2,2 см. Определить кинетическую и потенциальную энергию груза через
x = 2,2 см. Определить кинетическую и потенциальную энергию груза через  t = 3с после начала колебаний, если в начальный момент груз оттянут на
t = 3с после начала колебаний, если в начальный момент груз оттянут на  , см. Определить кинетическую, потенциальную и полную энергии точки через
, см. Определить кинетическую, потенциальную и полную энергии точки через  , см. Найти максимальную силу, действующую на точку, и полную энергию колеблющейся точки.
, см. Найти максимальную силу, действующую на точку, и полную энергию колеблющейся точки. = 45о.
= 45о. , м. Определите максимальные значения: 1) возвращающей силы; 2) кинетической энергии.
, м. Определите максимальные значения: 1) возвращающей силы; 2) кинетической энергии. , м. Определите: 1) возвращающую силу для момента времени
, м. Определите: 1) возвращающую силу для момента времени  .
. = 500 Гц. Определить частоту затухающих колебаний этой системы
= 500 Гц. Определить частоту затухающих колебаний этой системы  , если резонансная частота
, если резонансная частота  = 0,2.
= 0,2. . Смещение точки при t = 2Т составляет 5 см. Запишите уравнение этого колебания.
. Смещение точки при t = 2Т составляет 5 см. Запишите уравнение этого колебания. .
.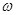 = 65 рад/с, а её добротность Q = 2. Определите собственную частоту колебаний
= 65 рад/с, а её добротность Q = 2. Определите собственную частоту колебаний  = 1 мин потеряло 40% своей энергии. Определите коэффициент сопротивления r.
= 1 мин потеряло 40% своей энергии. Определите коэффициент сопротивления r. собственных колебаний; 2) резонансную частоту
собственных колебаний; 2) резонансную частоту  . Найти частоту этих вынужденных колебаний. Чему равна частота собственных колебаний системы? При какой частоте внешней силы будет наблюдаться резонанс?
. Найти частоту этих вынужденных колебаний. Чему равна частота собственных колебаний системы? При какой частоте внешней силы будет наблюдаться резонанс? , см;
, см;  , см. Записать уравнение результирующего колебания.
, см. Записать уравнение результирующего колебания. и
и  , А = 5 см,
, А = 5 см, 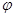 = 45о. Определите амплитуду результирующего колебания.
= 45о. Определите амплитуду результирующего колебания. , см и
, см и  , см. Определите уравнение траектории точки и вычертите её с нанесением масштаба.
, см. Определите уравнение траектории точки и вычертите её с нанесением масштаба. , см и
, см и  , см. Определите уравнение траектории точки и вычертите её с нанесением масштаба.
, см. Определите уравнение траектории точки и вычертите её с нанесением масштаба. . Напишите уравнение движения, получающегося в результате сложения этих колебаний, если начальная фаза одного из них равна нулю.
. Напишите уравнение движения, получающегося в результате сложения этих колебаний, если начальная фаза одного из них равна нулю. , см и
, см и  , см. Определите для результирующего колебания: 1) амплитуду; 2) начальную фазу. Запишите уравнение результирующего колебания и представьте векторную диаграмму сложения амплитуд.
, см. Определите для результирующего колебания: 1) амплитуду; 2) начальную фазу. Запишите уравнение результирующего колебания и представьте векторную диаграмму сложения амплитуд. , А. Определите: 1) период колебания; 2) емкость конденсатора; 3) максимальное значение на обкладках конденсатора; 4) максимальную энергию магнитного поля; 5) максимальную энергию электрического поля.
, А. Определите: 1) период колебания; 2) емкость конденсатора; 3) максимальное значение на обкладках конденсатора; 4) максимальную энергию магнитного поля; 5) максимальную энергию электрического поля.


