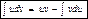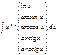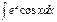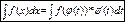- общее уравнение прямой
- общее уравнение прямой
 - каноническое уравнение прямой
- каноническое уравнение прямой
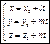 - параметрическое уравнение прямой
- параметрическое уравнение прямой
 - условие параллельности прямых
- условие параллельности прямых
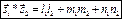 - условие перпендикулярности прямых
- условие перпендикулярности прямых
 - угол между прямыми
- угол между прямыми
Этапы перехода от общего уравнения прямой к каноническому:
1) Находится вектор  .
.
2) Находится точка М0 (x0, y0, z0), любая из этих координат приравнивается к 0,
оставшиеся координаты находятся из системы уравнений общего уравнения прямой.
3) Составляется каноническое или параметрическое уравнение прямой.
Производные.
(u±v)’=u’±v’; (uv)’ = u’v + uv’; (u/v)’ = u’v - uv’/v2
(un)’=n*un-1*u’; yx’=yt’/xt’; F’=-Fx’/Fy’; (f(u(x)))’=f’(u(x))*u’(x)
| функция
| произв-ая
| функция
| произв-ая
|
| k
|
| sin x
| cos x
|
| kx
| k
| cos x
| -sin x
|
| xn
| n*xn-1
| tg x
| 1/ cos2 x
|
| 1/x
| -1/x2
| ctg x
| -1/ sin2 x
|
| 1/xn
| -n/xn+1
| sin2 x
| sin 2x
|

| 1/2 
| cos2 x
| -sin 2x
|

| 
| arcsin x
| 
|
| logax
| 1/x*ln a
| arccos x
| 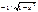
|
| ln x
| 1/x
| arctg x
| 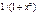
|
| ex
| ex
| arcctg x
| 
|
Таблица неопределенных интегралов
Подведение под знак дифференциала: 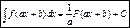
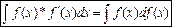
 Дифференциальные уравнения с пост-ми коэффициентами Дифференциальные уравнения с пост-ми коэффициентами
|
| №
| корни k2+pk+q=0
| вид общего решения
|
|
| D>0, k1≠k2
| 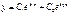
|
|
| D=0, k1=k2
| 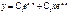
|
|
| D<0, k1/2=α±βi
| 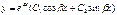
|
| №
| f(x)
| кратность корней
| вид yчаст.
|
|
| p*eαx (p-число)
| α≠k1, α≠k2
| A*eαx
|
| α=k1, α≠k2
| A*x*eαx
|
| α=k1, α=k2
| A*x2*eαx
|
|
| Pn(x)*eαx (Pn(x)-выражение)
| α≠k1, α≠k2
| (Anxn+An-1xn-1+…+A0)eαx
|
| α=k1, α≠k2
| (Anxn+…+A0)x*eαx
|
| α=k1, α=k2
| (Anxn+…+A0)x2*eαx
|
|
| Pn(x)
| k1≠0, k2≠0
| Anxn+An-1xn-1+…+A0
|
| k1=0 или k2=0
| (Anxn+…+A0)x
|
|
| Mcosβx+Nsinβx
| k1/2≠α±βi
| Acosβx+Bsinβx
|
| k1/2=α±β
| (Acosβx+Bsinβx)x
|
Методы интегрирования:
 I. Интегрирование по частям:
I. Интегрирование по частям: 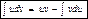
1) u = xn
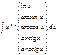
2) u = 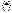

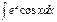
3) u = ex
II. Замена переменных: 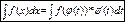
| Таблица первообразных
|
| функция
| первообразная
| функция
| первообразная
|
| xn (n≠-1)
| xn+1/n+1
| cos x
| sin x
|
| 1/ x
| ln x
| 1/sin2 x
| -ctg x
|
| 1/ xn
| -1/(n-1)*xn-1
| 1/cos2 x
| tg x
|
1/ 
| 2* 
| sin(kx+b)
| -1/k*cos(kx+b)
|
| k
| kx
| cos(kx+b)
| 1/k*sin(kx+b)
|
| ex
| ex
| (kx+b)n
| (kx+b)n+1/k(n+1)
|
| ax
| ax/ln a
| 1/kx+b
| 1/k*ln(kx+b)
|
| sin x
| -cos x
| ekx+b
| 1/k* ekx+b
|
|
|
|
|
|

 - общее уравнение прямой
- общее уравнение прямой - каноническое уравнение прямой
- каноническое уравнение прямой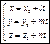 - параметрическое уравнение прямой
- параметрическое уравнение прямой - условие параллельности прямых
- условие параллельности прямых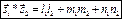 - условие перпендикулярности прямых
- условие перпендикулярности прямых - угол между прямыми
- угол между прямыми .
.



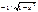
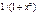




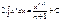


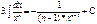






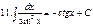


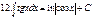

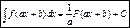
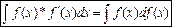
 Дифференциальные уравнения с пост-ми коэффициентами
Дифференциальные уравнения с пост-ми коэффициентами
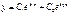
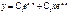
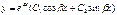
 I. Интегрирование по частям:
I. Интегрирование по частям: