Полные системы функций алгебры-логики.
Очевидно могут быть построены простейшие логические элементы, реализующие элементарные логические функции двух переменных f0,..., f15. Сложные логические функции могут быть построены последовательным выполнением функциональных зависимостей, связывающих пары переменных. Например, функция f (x1, x2, x3, x4) = (((x1·x1)
рис. 1.4 Следовательно, имея элементы, осуществляющие элементарные операции f0,..., f15 можно выполнить любую сложную логическую операцию. Такую систему можно назвать полной системой или базисом. Условие наличия 16 различных типов логических элементов, каждый из которых реализует одну из 16 элементарных функций f0,..., f15, является достаточным для синтеза логических устройств любой сложности, но оно не является необходимым, т.е. при синтезе можно ограничиться меньшим набором элементарных функций, взятых из f0,..., f15. Последовательно исключая из базиса функции, можно получить минимальный базис. Под минимальным базисом понимают такой набор функций, исключение из которого любой функции превращает полную систему функций в неполную. Возможны различные базисы и минимальные базисы, отличающиеся друг от друга числом входящих в них функций и видом этих функций. Выбор того или иного базиса для синтеза логических устройств связан с тем, насколько просто, удобно и экономично технически выполнить элементы, реализующие входящие в базис функции, и в целом все логическое устройство. Как показано выше, с помощью логических операций конъюнкции (И), дизъюнкции (ИЛИ) и инверсии (НЕ) можно выразить любую другую из элементарных функций f0,..., f15. Следовательно, эта совокупность логических функций образует базис. Это означает, что любая логическая функция, как бы сложна она не была, может быть представлена через логические операции И, ИЛИ, НЕ. Иначе, можно построить любое логическое устройство, имея лишь три типа логических элементов, выполняющих операции И, ИЛИ, НЕ. Базис И, ИЛИ, НЕ не является минимальным. Из этой совокупности функций можно исключить функцию И, либо функцию ИЛИ и оставшийся набор функций будет удовлетворять свойствам базиса. Действительно, если исключить функцию И, то операцию И можно выразить через оставшиеся операции ИЛИ и НЕ. Чтобы показать это, дважды инвертируем конъюнкцию и применем затем правило де Моргана.
Хотя операцию И и можно выразить через операцию И и можно выразить через операции ИЛИ и НЕ, но это сложно (требуется выполнение трех операций инверсии и одной операции ИЛИ), поэтому на практике используется не минимальный базис, включающий в себя все эти три функции И, ИЛИ, НЕ. Рассмотрим некоторые другие базисы. При этом выбранный набор логических функций будет удовлетворять свойствам базиса, если с помощью этого набора функций окажется возможным выразить функции И и НЕ (либо функции ИЛИ и НЕ). 1. Базис образует функция Шеффера (И-НЕ). Действительно операции НЕ и И следующим образом можно выразить через операции И-НЕ:
Таким образом, элементов одного типа, реализующих функцию И-НЕ, достаточно для построения логического устройства произвольной сложности. 2. Базис образует функция Вебба (ИЛИ-НЕ). Покажем, что операция НЕ и ИЛИ выражаются через операцию ИЛИ-НЕ.
Таким образом, используя однотипные элементы, реализующие операцию ИЛИ-НЕ, можно построить логическое устройство любой сложности. 3. Базис образуют функция запрета
В настоящее время базис И, ИЛИ, НЕ обычно используется при начальной стадии проектирования устройств для построения функциональной схемы. Для реализации устройств обычно используются базисы широко выпускаемые промышленностью в интегральном исполнении.
|

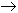 x3|x4) V x1 может быть получена с помощью схемы на рис. 1.4.
x3|x4) V x1 может быть получена с помощью схемы на рис. 1.4.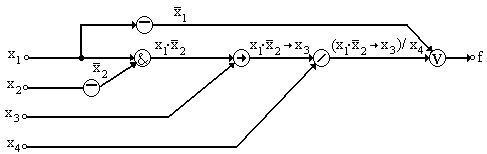
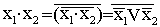
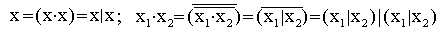
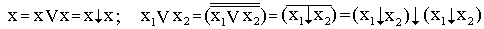
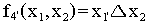 и константа единицы. Действительно,
и константа единицы. Действительно,



