Общие сведения. Задача № 3.Дана функция z = f(x,y)
Задача № 3. Дана функция z = f(x,y). Найти частные производные первого порядка. 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 3.10 3.11 3.12 3.13 3.14 3.15 3.16 3.17 3.18 3.19 3.20 3.21 3.22 3.23 3.24 3.25 3.26 3.27 3.28 3.29 3.30 Задание № 4. Найти неопределенные интегралы. Для удовлетворительной и хорошей оценки выполняется только задания а) - с), для отличной- все пункты. 1. а) 2. a) 3. a) 4. a) 5. a) 6. a) 7. a) 8. a) 9. a) 10. a) 11. a) 12. a) 13. a) 14. a) 15. a) 16. a) 17. a) 18. a) 19. a) 20. a) 21. a) 22. a) 23. a) 24. a) 25. a) 26. a) 27. a) 28. a) 29. a) 30. a) 31. a) 32. a)
Задание № 5. Найдите площадь фигуры, ограниченной линиями. Сделать чертеж. 1) y= 2) y= 3) y= 4) y= 5) y= 6) y= 7) y= 8) y= 9) y= 10) y= 11) y= 12) y= 13) y= 14) y= 15) y= 16) y= 17) y=x+5; y= 18) y=x+3; y= 19) y=x+4; y= 20) y= 21) y= 22) 4y= 23) y= 24) y= 25) y= 26) y= 27) y= 28) 29) y= 30) y=
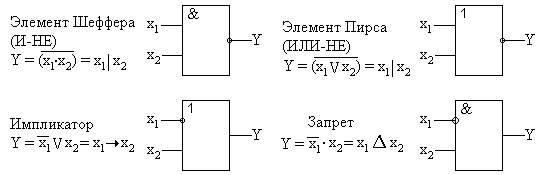
Задание № 6. Решить дифференциальное уравнение с разделяющимися переменными. 6.1. 6.2. 6.3. 6.4. 6.5. 6.6. 6.7. 6.8. 6.9. 6.10. 6.11. 6.12. 6.13. 6.14. 6.15. 6.16. 6.17. 6.18. 6.19. 6.20. 6.21. 6.22. 6.23. 6.24. 6.25. 6.26. 6.27. 6.28. 6.29. 6.30. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ Общие сведения. Выше отмечалось, что логические функции и их аргументы принимают значение лог.0 и лог.1. При этом следует иметь в виду, что в устройствах лог.0 и лог.1 соответствует напряжению определенного уровня (либо формы). Наиболее часто используется два способа физического представления лог.0 и лог.1: потенциальный и импульсный. При потенциальной форме (рис. 2.1,а и 2.1,б) для представления лог.0 и лог.1 используется напряжение двух уровней: высокий уровень соответствует лог.1 (уровень лог.1) и низкий уровень соответствует лог.0 (уровень лог.0). Такой способ представления значений логических величин называется положительной логикой. Относительно редко используют так называемую отрицательную логику, при которой лог.1 ставят в соответствии низкий уровень напряжения, а лог.0 - высокий уровень. В дальнейшем, если это не оговаривается особо, будем пользоваться только положительной логикой.
Заметим, что, если при потенциальной форме соответствующая сигналу информация (лог.1 либо лог.0) может быть определена практически в любой момент времени, то при импульсной форме соответствие между уровнем напряжения и значением логической величины устанавливается в определенные дискретные моменты времени (так называемые тактовые моменты времени), обозначенные на рис.2.1,в целыми числами t = 0, 1, 2,... Общие обозначения логических элементов.
|


















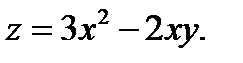



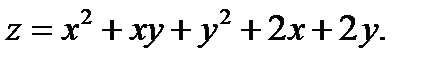







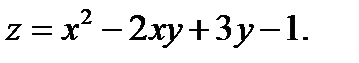
 b)
b)  с)
с)  d)
d) 

 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b) 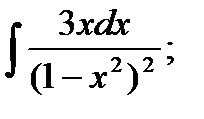 c)
c)  d)
d) 
 b)
b) 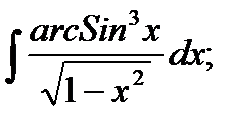 c)
c)  d)
d) 
 b)
b)  c)
c) 

 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
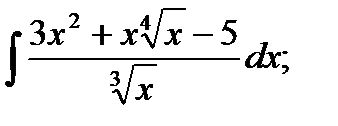 b)
b)  c)
c)  d)
d) 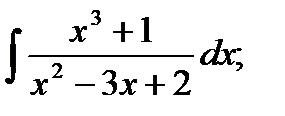
 b)
b)  c)
c)  d)
d) 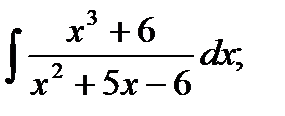
 b)
b) 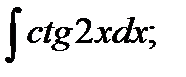 c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
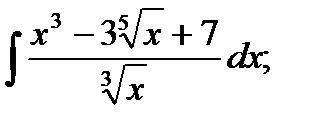 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 
 b)
b)  c)
c)  d)
d) 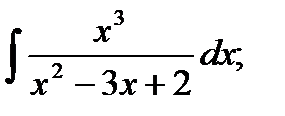
 b)
b) 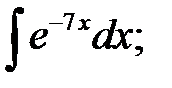 c)
c)  d)
d) 
 b)
b)  c)
c) 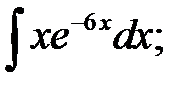 d)
d) 

 y=
y= 
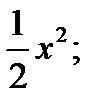 x+2y-6=0;
x+2y-6=0; y=
y= 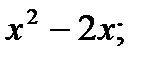
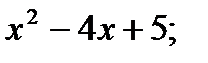 y=2;
y=2; y=2x;
y=2x; y=x+10;
y=x+10; y=
y= 
 y= 2x+2;
y= 2x+2; y=
y= 
 y= -2x+8;
y= -2x+8; y= x-1;
y= x-1; 3y-5x-25=0;
3y-5x-25=0; y=2x-10;
y=2x-10; 2x-y-8=0;
2x-y-8=0; y=2x-6;
y=2x-6; 2x-y-4=0;
2x-y-4=0;


 3y-3x-16=0;
3y-3x-16=0; y=
y= 
 4y=x+6;
4y=x+6; y+3x-4=0;
y+3x-4=0; y=0;
y=0; y=0;
y=0; x=0, y=0;
x=0, y=0; y=0;
y=0; y=3x;
y=3x; y=-2x+8;
y=-2x+8; y=
y= 



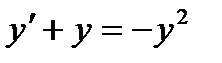








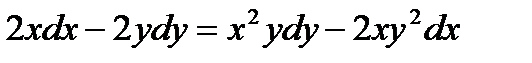
















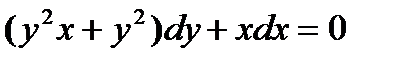
 При импульсной форме лог.1 соответствует наличие импульса, логическому 0 - отсутствие импульса (рис.2.1, в).
При импульсной форме лог.1 соответствует наличие импульса, логическому 0 - отсутствие импульса (рис.2.1, в).