и математическая статистика
351. Среди 25 студентов группы, в которой десять девушек, разыгрывается пять билетов. Определить вероятность того, что среди обладателей билетов окажутся две девушки. 352. В лотерее разыгрывается 1000 билетов. Среди них два выиграша по 500 руб., пять по 200 руб., десять по 100 руб. и 25 по 50 руб. Некто покупает один билет. Найти вероятность: 1) выигрыша не менее 200 руб.; б) какого-либо выигрыша. 353. Техническое устройство, состоящее из трёх узлов, работало в течение некоторого времени t. За это время первый узел оказывается неисправным с вероятностью 0,1, второй с вероятностью 0,15, третий – с вероятностью 0,05. Найти вероятность того, что за время работы хотя бы один узел технического устройства станет неисправным. 354. Студент разыскивает нужную ему формулу в трёх справочниках. Вероятность того, что формула содержится в первом, втором, третьем справочнике соответственно равна 0,6; 0,7; 0,8. Найти вероятность того, что формула содержится: а) только в одном справочнике; б) только в двух справочниках; в) во всех трёх справочниках. 355. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника – 0,9; для велосипедиста – 0,8; для бегуна – 0,75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму. 356. Имеется 3 коробки деталей, изготовленных заводом №1 и 2 коробки деталей, изготовленных заводом №2. Вероятность того, что деталь завода №1 стандартная равна 0,8, а завода №2 – 0,9. Сборщик наудачу извлёк деталь из наудачу взятой коробки. Найти вероятность того, что наудачу извлечённая деталь из наудачу взятого ящика стандартная. 357. В четырёх попытках разыгрываются некоторые предметы. Вероятность выиграша в каждой попытке равна 0,5. Какова вероятность выиграша трёх предметов? 358. Предприятие изготовило и отправило заказчику 100000 бутылок минеральной воды. Вероятность того, что бутылка может оказаться битой, равна 0,0001. Найти вероятность того, что в отправленной партии будет пять битых бутылок. 359. В микрорайоне девять машин технической службы. Для бесперебойной работы необходимо, чтобы не менее восьми машин были в исправном состоянии. Считая вероятность исправного состояния для всех машин одинаковой и равной 0,9, найти вероятность бесперебойной работы технической службы в микрарайоне. 360. Фирма рассылает рекламные проспекты восьми потенциальным партнерам. В результате такой рассылки в среднем у каждого пятого потенциального партнера возникает интерес к фирме. Найти вероятность того, что это произойдет не более чем в трёх случаях.
361 – 370. Дискретная случайная величина X может принимать только два значения: 361. 362. 363. 364. 365. 366. 367. 368. 369. 370.
371 – 380. Случайная величина Х задана функцией распределения
381 – 390. Известны математическое ожидание а и среднее квадратическое отклонение s нормально распределенной случайной величины Х. Найти вероятность попадания этой величины в заданный интервал (a; b). 381. 383. 385. 387. 389.
391 – 400. Найти доверительный интервал для оценки математического ожидания а нормального распределения с надежностью 0.95, зная выборочную среднюю х, объем выборки n и среднее квадратическое отклонение s.
|

 и
и  , причем
, причем  . Известны вероятность
. Известны вероятность  возможного значения
возможного значения  и дисперсия
и дисперсия  . Найти закон распределения этой случайной величины.
. Найти закон распределения этой случайной величины.




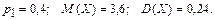




 . Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины.
. Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины.







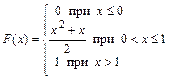

 382.
382. 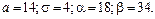
 384.
384. 
 386.
386. 
 388.
388. 
 390.
390. 













