ТЕМЫ КОНТРОЛЬНЫХ РАБОТ. 1. Дисперсия постоянной величины равна нулю, то есть
1. Дисперсия постоянной величины равна нулю, то есть
D (c) = 0 (21)
2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат, то есть D(cX) = c2D(X), (22) где c - постоянная величина 3. Дисперсия суммы (разности) конечного числа n независимых случайных величин равна сумме их дисперсий, то есть D(X1
4. Если X1, X2,..., Xn - одинаково распределенные независимые случайные величины, дисперсия каждой из которых равна s2, то дисперсия их суммы равна ns2, а дисперсия средней арифметической равна s2/n, то есть
D(X) = s2/n (24)
Для вычисления дисперсии проще пользоваться другой формулой, которая получается из формулы (20) путем несложных математических выкладок. D(X)=M[(X-M(X))2 ]=М[Х2-2М(Х)Х+(М(Х))2]=М(Х)2-2М(Х)М(Х)+ +(М(Х))2=М(Х2)-[М(Х)]2=М(Х2)-М2(Х) Формула для упрощенного вычисления дисперсии дискретной случайной величины s2 = D(X) = М(Х2) - М2(Х) (25)
Вычислим дисперсию случайной величины для примера 1, используя этот способ. Результаты оформим в виде рабочей таблицы.
Первая колонка в таблице - значения Х, вторая колонка - вероятности этих значений, третья есть результат произведения первой колонки на вторую и четвертая есть результат произведения первой колонки на третью (потому что х2Р(х) получается умножением х на х(Р(х)). Сумма значений третьей колонки дает ожидаемое среднее значение Х, а сумма значений четвертой колонки - ожидаемое среднее значение Х2. Затем, чтобы получить дисперсию Х, мы вычисляем разность М(Х2) - [М(Х)] 2 D(X) = М(Х2) - [М(Х)] 2 = 7,3 - (2,3)2 = 2,01 Результат совпал с тем, что мы получили, используя формулу (20).
s = Для примера 1 среднее квадратическое отклонение есть: s= В чем смысл дисперсии и среднего квадратического отклонения? Как мы можем интерпретировать их значения? По определению s2 - средний квадрат отклонения значений случайной величины от математического ожидания. Отсюда следует, что это мера рассеяния всех возможных значений случайной величины относительно среднего ожидаемого значения. Дисперсия характеризует колеблемость, изменчивость случайной величины: чем больше вариация, тем дальше от средней находятся возможные значения случайной величины. Для содержательной интерпретации зачастую полезно применять значение, которое дает корень квадратный из дисперсии - среднее квадратическое отклонение (стандартное отклонение). Если сравнивают две случайные величины, то та из них, которая имеет большую дисперсию и среднее квадратическое отклонение, более вариабельна. Риск, ассоциируемый с инвестициями, часто измеряют стандартным отклонением возврата инвестиций. Если сравниваются два типа инвестиций с одинаковой ожидаемой средней возврата, то инвестиции с более высоким средним квадратическим отклонением считаются более рискованными (хотя более высокое стандартное отклонение предполагает возврат более вариабельный с обеих сторон - как ниже, так и выше средней). [1] Дискретные случайные величины называются одинаково распределенными, если у них одинаковые ряды распределения, а, следовательно, и одинаковые числовые характеристики ТЕМЫ КОНТРОЛЬНЫХ РАБОТ ПО ПРЕДМЕТУ «КРИМИНАЛИСТИКА» Выбор варианта контрольной работы осуществляется в соответствии с номером в журнале учета успеваемости и посещаемости (11-му номеру по списку соответствует первый номер варианта контрольной работы и т. д.) ВАРИАНТ № 1.
|

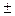 Х2 ± ¼ ± Хn) = D(X1) ± D(Х2 ) ± ¼ ± D(Хn) (23)
Х2 ± ¼ ± Хn) = D(X1) ± D(Х2 ) ± ¼ ± D(Хn) (23)
 Среднее квадратическое отклонение (стандартное) отклонение дискретной случайной величины равно корню квадратному из дисперсии, обозначается как s или S(X)
Среднее квадратическое отклонение (стандартное) отклонение дискретной случайной величины равно корню квадратному из дисперсии, обозначается как s или S(X) (26)
(26) =1,418.
=1,418.


