Такое представление чисел обозначает вот такое число:  , где
, где  — цифры, а
— цифры, а  — основание системы счисления.
— основание системы счисления.
Посмотрим чему равны числа из примеров. Используем только что приведённую формулу:
Мы разобрали, как узнать, чему равно число в любой системе счисления. Но как нам получить это число? Представим что у нас есть некоторое число  , и мы хотим получить его представление в системе по основанию
, и мы хотим получить его представление в системе по основанию  . Как нам это сделать?
. Как нам это сделать?
Мы знаем, что число  можно представить в виде
можно представить в виде  , будем из этого исходить. Что будет, если мы поделим это число на
, будем из этого исходить. Что будет, если мы поделим это число на  . Получим
. Получим

и остаток от деления  . Почему
. Почему  ? Все члены суммы делятся на
? Все члены суммы делятся на  без остатка, а последний член
без остатка, а последний член  в результате деления даёт
в результате деления даёт  и
и  в остатке, так как максимальное значение цифры всегда на единичку меньше основания системы. Итак мы получили самую правую цифру
в остатке, так как максимальное значение цифры всегда на единичку меньше основания системы. Итак мы получили самую правую цифру  , как остаток от деления, и число
, как остаток от деления, и число  , как результат деления числа
, как результат деления числа  на
на  . Если мы так будем продолжать делить, то получим все цифры
. Если мы так будем продолжать делить, то получим все цифры  .
.
Возьмём для примера полюбившееся нам число  и получим представление этого числа в двоичной системе счисления:
и получим представление этого числа в двоичной системе счисления:
-
 , остаток
, остаток  ;
; -
 , остаток
, остаток  ;
; -
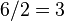 , остаток
, остаток  ;
; -
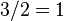 , остаток
, остаток  ;
; -
 , остаток
, остаток  .
.
Что и следовало ожидать, получили:  .
.
Представим число 25 в троичной системе счисления:
-
 , остаток
, остаток  ;
; -
 , остаток
, остаток  ;
; -
 , остаток
, остаток  .
.
Получили число:  .
.
Для закрепления наших знаний проделаем вычисления для восьмеричной и десятичной систем счисления.
Восьмеричная система счисления:
Результат:  .
.
Десятичная система счисления:
Результат:  .
.
Чтобы ещё лучше понять перевод в различные системы счислений, посмотрим, какие трансформации происходят внутри числа  .
.
Представим это число в виде
 .
.
Посмотрим, что у нас получится при последовательном делении на  :
:
- делим на
 , получаем
, получаем  и
и  в остатке;
в остатке; - делим ещё раз на
 , получаем
, получаем  и
и  в остатке;
в остатке; - и ещё раз делим на
 , получаем
, получаем 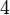 и
и  в остатке;
в остатке; - делим в последний раз на
 , получаем
, получаем  и
и 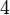 в остатке.
в остатке.

 , где
, где  — цифры, а
— цифры, а  — основание системы счисления.
— основание системы счисления. ;
;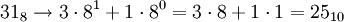 ;
; ;
; .
. , и мы хотим получить его представление в системе по основанию
, и мы хотим получить его представление в системе по основанию  , будем из этого исходить. Что будет, если мы поделим это число на
, будем из этого исходить. Что будет, если мы поделим это число на 
 . Почему
. Почему  и
и  , как результат деления числа
, как результат деления числа  .
. и получим представление этого числа в двоичной системе счисления:
и получим представление этого числа в двоичной системе счисления: , остаток
, остаток  ;
; , остаток
, остаток 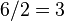 , остаток
, остаток 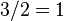 , остаток
, остаток  , остаток
, остаток  .
. , остаток
, остаток  , остаток
, остаток  ;
; , остаток
, остаток  .
.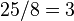 , остаток
, остаток  , остаток
, остаток  .
. .
. , остаток
, остаток  ;
; , остаток
, остаток  .
. .
. .
. :
: и
и  в остатке;
в остатке; и
и  в остатке;
в остатке;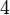 и
и 


