Верхняя оценка вероятности ошибки и вероятности ошибки на бит

Где – SNR(Signal noise ratio) отношение сигнал-шум, q – кол-во сигналов.

 

Вероятность ошибки на бит как функция от отношения сигнал/шум на бит задается выражением

 

Исходя из формулы (10) получим, что верхняя оценка для равна

В нашем случае, так как q = 4, то

 

 

Лабораторная работа выполнялась в среде Matlab 2009.

Листинг программы:

clear all

clc;

%================== Global values ===================================

lines = 1;

default_general = {'10','600','1200','1200','45'};

param_general = inputdlg({'Мощность сигнала',...

'Модуляционная скорость',...

'Информационная скорость',...

'Частота несущей',...

'Начальный фазовый сдвиг'},...

'Введите основные данные',...

1,default_general);

 

Esig = str2num([param_general{1}]);

Vmod = str2num([param_general{2}]); % Modulation Rate, Bod

Vinf = str2num([param_general{3}]); % Information Rate, bit/s

Fc = str2num([param_general{4}]); % Carrier Frequency, Gz

ThetaShift = str2num([param_general{5}])*pi/180;

%---------Missing values-------------------------

T = 1/Vmod; % Period of signals

Tc = 1/Fc; % Period of the carrier signal.

q = 2^round(Vinf*T); % Number of signals

Amp = sqrt(2*Esig/T); % Amplitude

%---------Additional values----------------------

lines = 1;

default_addit = {'16','32','10','20','8','25','0.5','1000','1000','7'};

param_addit = inputdlg({ 'Длина последовательности','Дискретизация',...

'Точность спектра', 'Макс. число ошибок',...

'SHR начальное',...

'SHR конечное','SHR инкремент',...

'Кол-во повторений для "облака"',...

'Кол-во повторений для статистики',...

'SNR для примера'},...

'Введите дополнительные данные',1,default_addit);

LENGHT = str2num([param_addit{1}]);

OVERSAMPL = str2num([param_addit{2}]);

WIDTHFREQ = str2num([param_addit{3}]);

count_errMax= str2num([param_addit{4}]);

SNRstart = str2num([param_addit{5}]);

SNRfinish = str2num([param_addit{6}]);

SNRincr = str2num([param_addit{7}]);

Nrun = str2num([param_addit{8}]);

REPEAT = str2num([param_addit{9}]);

ExSNR = str2num([param_addit{10}]);

 

deltaT = Tc/OVERSAMPL;

TIME = 0:deltaT:T;

StepF = Fc/OVERSAMPL;

LeftRangeF = -Fc-WIDTHFREQ*Fc;

RightRangeF = Fc+WIDTHFREQ*Fc;

FREQ = LeftRangeF:StepF:RightRangeF;

nfig = 1; % счетчик графиков и рисунков

InitRand = 13517;% начальная установка псевдослучайного генератора

delta = pi/q;

 

COLORR = rand(1,q);

COLORG = rand(1,q);

COLORB = rand(1,q);

%==========================================================================

 

%I

signals = zeros(q, length(TIME)); %array of signals

theta = zeros(1,q); %phase shift

for i=0: q-1

theta(i+1) = mod(ThetaShift+(2*pi/q)*i, 2*pi);

signals(i+1,:)= Amp*cos(2*pi*Fc*TIME + theta(i+1));

end

Title = ['PSK, q = ', int2str(q),', f_0 = ', num2str(Fc), ' Gz'];

figure(nfig); clf; nfig = nfig + 1;

hold on

for i=0:q-1

hPlot = plot(TIME, signals(i+1,:));

set(hPlot,'Color',[COLORR(i+1),COLORG(i+1),COLORB(i+1)]);

hText=text(0,Amp*1.3-i*2.6*Amp/q,['Theta:', num2str(theta(i+1)*180/pi,4)]);

set(hText,'Color',[COLORR(i+1),COLORG(i+1),COLORB(i+1)]);

end

hold off

grid on

xlabel('Time')

ylabel('Amplitude')

title(Title, 'FontName', 'Arial Cyr', 'FontSize', 9);

 

%--------------------Calculation Signal Spectrum --------------------------

%G = Amp*T*sin(pi*Fc*t)/(pi*Fc*t) = Amp*T*sinc(Fc*t);

spectrum = zeros(q,length(FREQ));

for i=0:q-1

spectrum(i+1,:) = (Amp*T/2)*(sinc((FREQ-Fc)*T)*exp(1i*theta(i+1)) +...

sinc((FREQ+Fc)*T)*exp(-1i*theta(i+1)));

end

figure(nfig); nfig = nfig + 1;

clf;

nonnegative = find(FREQ>=0);

h = round(sqrt(q));

w = ceil(q/h);

title('Амплитудные спектры', 'FontName', 'Arial Cyr', 'FontSize', 9);

for i=0:q-1

subplot(w,h,i+1)

hPlot = plot(FREQ(nonnegative), abs(spectrum(i+1, nonnegative)));

set(hPlot,'Color',[COLORR(i+1),COLORG(i+1),COLORB(i+1)]);

hLeg = legend(['Theta:', num2str(theta(i+1)*180/pi,4)]);

set(hLeg,'Color',[COLORR(i+1),COLORG(i+1),COLORB(i+1)]);

grid on

xlabel('Frequence')

ylabel('Amplitude')

end

 

%----------------------Formating Signal Sequence--------------------------

IndexRandSet = fix((q)*rand(1,LENGHT));

TimeSequence = zeros(1,LENGHT*signals(1,:));

SignalSequence = zeros(1,LENGHT*T);

 

figure(nfig); clf; nfig = nfig + 1;

subplot(3,1,1)

for k = 1:LENGHT

index = IndexRandSet(k)+1;

SignalSequence = [SignalSequence, signals(index,:)];

TimeSequence = [TimeSequence, TIME+(k-1)*(T+deltaT)];

hPlot = plot(TIME+(k-1)*(T+deltaT), signals(index,:));

set(hPlot,'Color',[COLORR(index),COLORG(index),COLORB(index)]);

hold on

grid on

end

title('Последовательность ФМ сигналов','FontName','Arial Cyr','FontSize', 9);

 

SpectrSequence = zeros(1,length(FREQ));

for k = 1:LENGHT

SpectrSequence = SpectrSequence + spectrum(IndexRandSet(k)+1,:)...

.*exp(-(1i*2*pi*(k-1)*T)*FREQ);

end

subplot(3,1,[2,3])

plot(FREQ(nonnegative), abs(spectrum(0+1,nonnegative)),...

FREQ(nonnegative), abs(SpectrSequence(nonnegative))/LENGHT);

grid on

title('Спектр одиночного ФМ сигнала и спектр последовательности сигналов',...

'FontName', 'Arial Cyr', 'FontSize', 9);

 

hl = legend('Спектр одиночного сигнала', 'Спектр последователности сигналов');

set(hl, 'FontName', 'Arial Cyr', 'FontSize', 9);

 

hold off

title('Спектр Последовательности ФМ сигналов', 'FontName','Arial Cyr',... 'FontSize', 9);

 

%===II===

%---------------------Signal Constellation--------------------------------

basisFunction1 = sqrt(2/T)*cos(2*pi*Fc*TIME);

basisFunction2 = sqrt(2/T)*sin(2*pi*Fc*TIME);

basisFunction1 = basisFunction1/norm(basisFunction1);

basisFunction2 = basisFunction2/norm(basisFunction2);

 

figure(nfig); clf; nfig = nfig + 1;

 

plot(TIME, basisFunction1,TIME, basisFunction2);

title('Базисные функции', 'FontName', 'Arial Cyr', 'FontSize', 9);

legend('cos','sin');

grid on;

 

signal_points1 = zeros(1,q);

signal_points2 = zeros(1,q);

 

figure(nfig); clf; nfig = nfig + 1;

subplot(1,2,1)

title('Множество сигнальных точек', 'FontName', 'Arial Cyr', 'FontSize', 9);

hold on

 

for i=0:q-1

signal_points1(i+1) = signals(i+1,:)*basisFunction1';

signal_points2(i+1) = signals(i+1,:)*basisFunction2';

hPlot = plot(signal_points1(i+1),signal_points2(i+1),'o');

set(hPlot,'Color',[COLORR(i+1),COLORG(i+1),COLORB(i+1)]);

set(hPlot,'LineWidth', 4);

end

grid on

axis('square');

 

%TEST

bF1 = sqrt(2/T)*cos(2*pi*Fc*TIME+delta);

bF2 = sqrt(2/T)*sin(2*pi*Fc*TIME+delta);

bF1 = bF1/norm(bF1);

bF2 = bF2/norm(bF2);

for i=0:q-1

sp1 = signals(i+1,:)*bF1';

sp2 = signals(i+1,:)*bF2';

x_ =0:sp1/100:round(sp1*1.4);

range = zeros(1, length(x_));

if mod(atan2(sp2,sp1),pi/2)>0.01

range = sp2/sp1 * x_;

plot(x_, range,'k');

end

end

hold off

 

%-------------Modeling of transmission over a noisy channel.--------------

rand('seed', InitRand);

subplot(1,2,2)

axis('square');

% SNR = E/No, SNR - signal to noise ratio

SNRMin = 10^(SNRstart/10);

SNRMax = 10^(SNRfinish/10);

E = norm(signals(1,:))^2;

DispNoiseMin = E/(2*SNRMin); % noise dispertion

SigmaDispNoiseMin = sqrt(DispNoiseMin); % noise standard deviation

DispNoiseMax = E/(2*SNRMax);

SigmaDispNoiseMax = sqrt(DispNoiseMax);

% r - received signal, s - original signal, n - noise

rMin1 = zeros(1, Nrun);

rMin2 = zeros(1, Nrun);

rMax1 = zeros(1, Nrun);

rMax2 = zeros(1, Nrun);

for l = 1:Nrun

i = fix((q)*rand);

nMin = SigmaDispNoiseMin*randn(size(TIME));

nMax = SigmaDispNoiseMax*randn(size(TIME));

rMin = signals(i+1,:) + nMin;

rMax = signals(i+1,:) + nMax;

rMin1(l) = rMin*basisFunction1';

rMin2(l) = rMin*basisFunction2';

rMax1(l) = rMax*basisFunction1';

rMax2(l) = rMax*basisFunction2';

end

hold on

plot(rMin1,rMin2,'y.', rMax1,rMax2,'b.');

legend(['SNR(Дб)=',num2str(SNRstart)],['SNR(Дб)=',num2str(SNRfinish)])

for i=0:q-1

hPlot = plot(signal_points1(i+1), signal_points2(i+1));

set(hPlot,'LineWidth', 2);

set(hPlot,'Color',[COLORR(i+1),COLORG(i+1),COLORB(i+1)]);

end

grid on

hold off

title('Облака рассеяния', 'FontName', 'Arial Cyr', 'FontSize', 9);

axis('square');

 

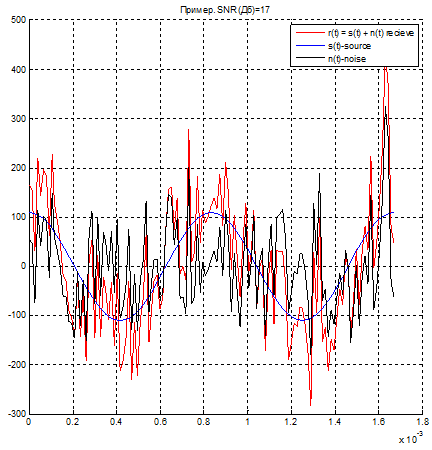
figure(nfig); clf; nfig = nfig + 1;

n = sqrt(E/(2*(10^(ExSNR/10))))*randn(size(TIME));

r = signals(1,:) + n;

title(['Пример. SNR (Дб)=',num2str(ExSNR)],'FontName','Arial Cyr','FontSize', 9);

hold on

hPlot = plot(TIME, r, 'r'); %recieve signal

set(hPlot, 'LineWidth', 2);

plot(TIME, signals(1,:),'b') %source signal

plot(TIME, n, '-k') %Noise

 

hl = legend('r(t) = s(t) + n(t) recieve','s(t)-source', 'n(t)-noise');

set(hl, 'FontName', 'Arial Cyr', 'FontSize', 9);

axis('square');

grid on

hold off

%===III===

%---------------------modeling the optimal receiver------------------------

figure(nfig); clf; nfig = nfig + 1;

SNRstart = 1;

Pe = zeros(size(SNRstart: SNRincr: SNRfinish));% error probability

Pe_theor = zeros(size(SNRstart: SNRincr: SNRfinish));

k = 1;

RzoneSize = (2*pi)/q;

for SNRdB = SNRstart: SNRincr: SNRfinish

SNR = 10^(SNRdB/10);

DispNoise = E/(2*SNR); % noise dispertion

SigmaDispNoise = sqrt(DispNoise); % noise standard deviation

count_experements = 0;

count_err = 0;

while (count_err < count_errMax && count_experements < REPEAT)

i = fix((q)*rand);

n = SigmaDispNoise*randn(size(TIME));

r = signals(i+1,:) + n;

r1 = r*basisFunction1';

r2 = r*basisFunction2';

 

delta = pi/q;

angle = atan2(r2,r1);

angle = mod(angle+ThetaShift,2*pi);

i_ = mod(q-round((angle)/RzoneSize),q);

if i_< 0 _ = i_+ q; end

if i_ ~= i _err = count_err + 1; end

 

count_experements = count_experements+1;

end % while(count_err < count_errMax)

 

Pe(k) = count_err/count_experements;

if q == 2

Pe_theor(k) = qfunc(sqrt(2*SNR)*sin(pi/q));

else

Pe_theor(k) = 2*qfunc(sqrt(2*SNR)*sin(pi/q));

end

 

if Pe(k)<10^(-9) break; end;

k=k+1;

end%SNR

semilogy(SNRstart: SNRincr: SNRfinish, Pe, 'r*', SNRstart: SNRincr: SNRfinish, Pe_theor,'bo');

legend('моделированная','теоретическая');

title('Вероятость ошибки (результаты моделирования и теоретическая)', 'FontName', 'Arial Cyr', 'FontSize', 9)

hx = xlabel('SNR, дБ');

set(hx, 'FontName', 'Arial Cyr', 'FontSize', 9)

hy = ylabel('PEB');

set(hy, 'FontName', 'Arial Cyr', 'FontSize', 9)

grid on