Индуктивный характер сигнальной связи.
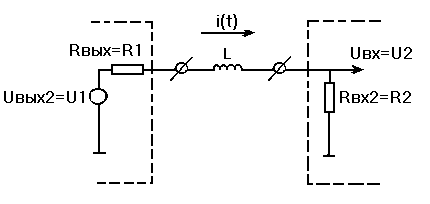
Эквивалентная схема соединения 2-х элементов Э1 и Э2 в этом случае представлена на рис. 1
Рис.1 Эквивалентная схема с индуктивной связью, где Э1 – источник, Э2 – приемник наводок. Пусть на выходе источника Э1 имеется ступенька напряжения (рис. 2)
Рис. 2. Ступенька напряжения на источнике Э1. При t=t0 по цепи рис. 1 потечет ток i(t) и тогда можно записать
где R1 выходное сопротивление источника, R2 – входное сопротивление приемника, L – индуктивность связи между ними. Определим реакцию приёмника Э2 на ступеньку напряжения источника Э1. Для этого необходимо знать Uвх=i(t)·R2 и, следовательно, знать значение тока i(t). Решение уравнения (1) для определения тока i(t) возможно несколькими способами. а) Классический метод решения. Ток представляют в виде двух составляющих
где i(t)св и i(t)пр – свободная и принудительная составляющие тока. В стационарном режиме
iсв ищется из уравнения (1) при iпр=0, когда U1=0. В этом случае
Возможен интеграл от обеих частей
Обозначим
Подставляя значение (9) в (2), имеем
Найдём С. При t=0 i=0. Тогда
Подставляя С в (10), уравнение (1) перепишется в виде
б) Операторный метод решения. Идея операторного метода заключается в том, что из области функций действительного переменного решения переносится в область функций комплексного переменного, где операции принимают более простой вид. После выполнения операций над функциями комплексного переменного производится обратный переход в области функций действительного переменного. Имеем Функцию f(t) – оригинал. F(P) – изображение
Найдем, например, изображение функции
Рис. 3. Функция Оно имеет вид
Если Таким образом, вычисляются изображения многих функций и составляются таблицы, например:
Производная f(t), т.е. Интеграл f(t), т.е. Запишем 1-е уравнение для изображений через ток, т.е.
где Отсюда
Прейдем от изображения к оригиналу. Для этого пользуются теоремой разложения, которая по-разному записывается для различных случаев. Чтобы определить эти случаи, анализируют выражение Тогда
где n – число корней, не равных нулю; Pk – не равные нулю корни; F3 – производная F3. Проиллюстрируем всё сказанное для эквивалентной схемы с индуктивной связью. У нас F2(P)=P[(R2+R1)+L*P], F2(P)=0, P=0. (17) Есть один, равный нулю, тогда для нахождения корней приравняем нулю F3(P)
отсюда
Обозначим тогда
Подставим (18) в (16), тогда получим
Имеем: F1(0)=U1; F3(0)=R2+R1; F1(Pk)=U1; F’3(P)=L, и эти выражения подставим в оригинал формулы разложения
Для напряжения U2(t) получим:
Это выражение совпадает с выражением уравнения (13). Проанализируем их.
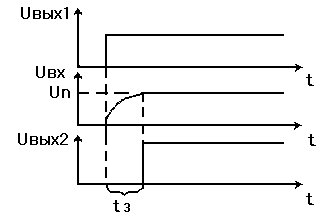
Рис. 4. Напряжение на входе источника и на выходе приемника. При подаче на вход схемы ступеньки напряжения Uвых. элемент Э2 срабатывает, когда на его входе Uвх2 достигает порога срабатывания Ип, т.е. с некоторой задержкой t =t 3 (Рис. 4). Величина t 3=0,7*L/Rвх2 определяется путем несложных расчетов. Для уменьшения задержки необходимо уменьшить индуктивность линии и увеличивать входное сопротивление элементов. Индуктивность линии связи зависит от типа используемых проводников, их сечения и длины. В современной радиоаппаратуре III и IV поколений используется элементы со временем переключения (задержки) в доли наносекунд. Желательно, чтобы эта задержка составляла малую, в худшем случае соизмеримую часть от времени переключения элементов.
|

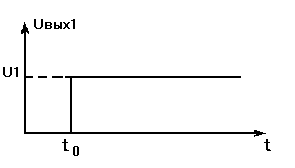
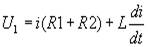 , (1)
, (1)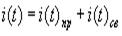 , (2)
, (2)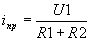 (3)
(3)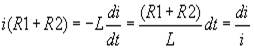 (4)
(4)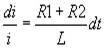 (5)
(5) (6)
(6)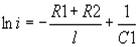 (7)
(7) (8)
(8)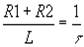 . В этом случае
. В этом случае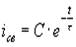 (9)
(9)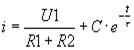 (10)
(10)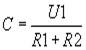 (11)
(11) (12)
(12) (13)
(13)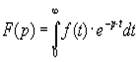 - прямое преобразование Лапласа.
- прямое преобразование Лапласа.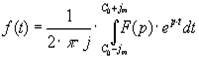 - обратное преобразование Лапласа.
- обратное преобразование Лапласа. , изображенной на рис 3.
, изображенной на рис 3.
 .
.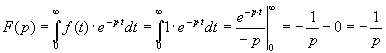
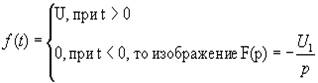 .
.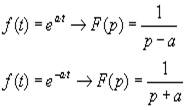
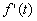 есть
есть 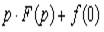
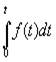 есть
есть 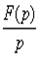 и т.д. (см. преобразования Лапласа.)
и т.д. (см. преобразования Лапласа.)
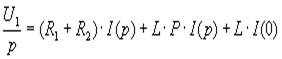 , (14)
, (14)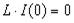
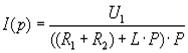 (15)
(15)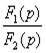 , т.е. i(t) представляют в виде дроби. Затем приравнивают знаменатель F2(p)=p·F3(p) и равные нулю корни определяют, приравнивая F3(p) к нулю;
, т.е. i(t) представляют в виде дроби. Затем приравнивают знаменатель F2(p)=p·F3(p) и равные нулю корни определяют, приравнивая F3(p) к нулю;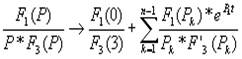 , (16)
, (16)
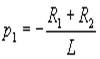
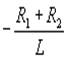 как
как 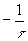 , т.е.
, т.е. 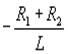 =
= 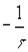
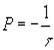 (18)
(18)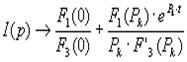 (19)
(19) (20)
(20)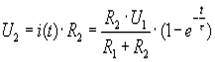 (21)
(21)