Системы линейных алгебраических уравнений
Лабораторная работа 2 Тема: Линейные системы. Фундаментальная система решений. Применения теоремы Кронекера-Капелли. Цель: оказание студентам помощи в овладении навыками решения задач, отражающих тематику данной лабораторной работы; научить студентов исследовать СЛАУ, применяя теорему Кронекера-Капелли, и находить фундаментальную систему решения. Теоретическое обоснование Системы линейных алгебраических уравнений Система
где Система (1) называется однородной, если все её свободные члены Решением системы называется такая совокупность Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если решений нет. Совместная система называется определённой, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. Две системы уравнений называются равносильными или эквивалентными, если они имеют одно в тоже множество решения. С помощью элементарных преобразований системы уравнений (например, умножение обеих частей уравнения на числа не равные нулю; сложение уравнений системы) получается система равносильная данной. Теорема (Кронекера - Капелли): Для того чтобы система (1)
расширенной матрицы (А, В) системы (1) были равны, т. е. Исследовать систему линейных уравнений означает определить, совместна она или нет, а для совместной системы, – выяснить определена она или нет. При этом возможны три варианта: 1) Если 2) Если 3) Если Для исследования систем линейных уравнений и нахождения их решений можно использовать метод Гаусса. Пусть дана однородная система линейных уравнений:
или в матичной форме Однородная система всегда совместна, так как существует тривиальное решение
|

 линейных уравнений с
линейных уравнений с  переменными имеет вид:
переменными имеет вид: (1)
(1) (
(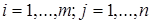 ) – произвольные числа называющиеся коэффициентами при переменных, а
) – произвольные числа называющиеся коэффициентами при переменных, а  – свободными членами уравнений.
– свободными членами уравнений. ,
,  , …,
, …,  , при подстановке которых данное уравнение системы обращается в верное равенство.
, при подстановке которых данное уравнение системы обращается в верное равенство.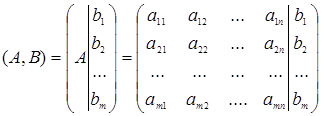
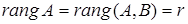 .
. , то система несовместна.
, то система несовместна. (где
(где  , то система совместна и неопределена.
, то система совместна и неопределена.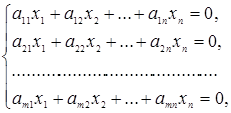 (2)
(2) .
. . однородная система неопределена тогда и только тогда, когда
. однородная система неопределена тогда и только тогда, когда  .
.


