Пример 3. Найти общее решение системы линейных уравнений методом Гаусса, выделив базисные неизвестные, и одно частное решение.
Найти общее решение системы линейных уравнений методом Гаусса, выделив базисные неизвестные, и одно частное решение.
Решение Проведем элементарные преобразование расширенной матрицы системы по методу Гаусса:
     
 
    ~  ~  ~
~ Из последней ступенчатой системы видно, что ранг матрицы системы равен Количество базисных переменных равно Запишем систему, соответствующую полученной матрице:
Из третьего уравнения выражаем
Придавая свободным переменным любые значения, будем получать частные решения системы. Частным решением системы будет являться решение Вопросы для защиты работы 1. Однородные и неоднородные системы. 2. Совместные и несовместные системы. 3. Что называется решением системы? 4. Сформулировать теорему Кронекера-Капелли. 5. Что означает «исследовать систему уравнений»? 6. Что можно сказать о множестве решений системы линейных уравнений, если ранг 7. Фундаментальная система решений?
|
.
, ранг расширенной матрицы равен 
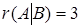, а количество переменных равно 
, так как 
, то система совместна и неопределена.
. В качестве главных переменных можно выбрать 
, 
и 
, соответствующие столбцам ненулевого минора третьего порядка: 
, в качестве свободных переменных – 
и 
.
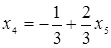. Подставляя это выражение во второе уравнение, получим: 
. Подставляя выражения для 
. Обозначив 
, а 
получим общее решение системы
.
матрицы этой системы и ранг 
расширенной матрицы равны нулю?
