Студент должен понимать, какие процессыисследуются в данной лабораторной работе, какие физические величины необходимо измерить.
Студент должен знать, как делать измерения и какими приборами необходимо пользоваться.
Студент должен уметь, работать с физическими приборами, произвести измерения, сделать вычисления по полученным данным работы. Если требует задание построить графики функциональных зависимостей. Определить абсолютную и относительную погрешность полученных измерений, сделать выводы
Контрольные вопросы
- Что называют узлом цепи?
- Первое правило Кирхгофа. Следствием какого закона оно является?
- Второе правило Кирхгофа. Следствием какого закона оно является?
- Принципиальная схема измерительного моста сопротивлений. Указать
ветви и плечи моста. - Схема мостика Уитстона. Ее отличие от принципиальной схемы.
- При каком условии мостик Уитстона считается сбалансированным?
- Сделайте вывод расчетной формулы для определения сопротивления по методу мостика Уитстона.
- Чем объяснить использование в данной работе контактного ключа?
- Объясните необходимость использования в данной работе нуля.
- Используя расчетную формулу для определения сопротивления, выведите формулу относительной погрешности.
- Какими преимуществами обладает метод определения сопротивления мостиком Уитстона по сравнению с методом амперметра и вольтметра?
- Изменится ли условие равновесия моста, если гальванометр и источник тока поменять местами?
- При каком положении реохорда погрешность измерения будет минимальной?
- Объясните устройство и порядок измерения сопротивлений с помощью
универсального мостика типа МО-47.
Линейный выЧислительный процесс
1. Период колебания маятника длиной L вычисляется по формуле: 
 , где g-ускорение свободного падения (9.81м/с2). Найти период колебаний маятника.
, где g-ускорение свободного падения (9.81м/с2). Найти период колебаний маятника.
2. Сила притяжения F между телами массами m1 и m2, находящимися на расстоянии r друг от друга, равна: 
 , где гравитационная постоянная g=6.673·1011м3/(кг·с2). Найти силу притяжения F.
, где гравитационная постоянная g=6.673·1011м3/(кг·с2). Найти силу притяжения F.
3. Периметр p правильного n-угольника, описанного около окружности радиусом r, равен: 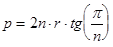 . Найти периметр р.
. Найти периметр р.
4. Энергия Е, излучаемая черным телом на волне длинной l при температуре t, равна:  , где с=2,997924·10
, где с=2,997924·10 
 -
-  скорость света; h=6,626·10-34 Дж/c - постоянная Планка; b=1,38· 10-23 Дж/град - постоянная Больцмана. Найти энергию Е, излучаемую черным телом.
скорость света; h=6,626·10-34 Дж/c - постоянная Планка; b=1,38· 10-23 Дж/град - постоянная Больцмана. Найти энергию Е, излучаемую черным телом.
5. Объем цилиндра с радиусом основания R и высотой Н равен: 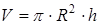 . Площадь его боковой и полной поверхностей соответственно равны:
. Площадь его боковой и полной поверхностей соответственно равны:  ,
,  . Найти V, Sб и Sn.
. Найти V, Sб и Sn.
6. Найти длину окружности, площадь круга и объем шара одного и того же радиуса R. При вычислении использовать формулы:  ,
,  ,
,  .
.
7. Определить скорость резания кругло шлифовального станка:  , где d1 - диаметр шкива двигателя, d2 - диаметр рабочего вала, d3 - диаметр режущего инструмента, z - частота вращения.
, где d1 - диаметр шкива двигателя, d2 - диаметр рабочего вала, d3 - диаметр режущего инструмента, z - частота вращения.
8. Вычислить общую поверхность и объем круглого конуса, имеющего радиус R и длину образующей L. При вычислении использовать формулы:  ,
,  , где Н - высота конуса, определяемая по формуле:
, где Н - высота конуса, определяемая по формуле:  .
.
9. Дана окружность радиуса r. Найти площади сегмента и сектора. При вычислении использовать формулы:  ,
,  , где a - центральный угол в градусах.
, где a - центральный угол в градусах.
10. Даны гипотенуза и катет прямоугольного треугольника. Найти второй катет и радиусы описанной и вписанной окружностей R и r. При вычислении использовать формулы:  ,
,  , где a, b, c - стороны треугольника, S - площадь.
, где a, b, c - стороны треугольника, S - площадь.
11. Вычислить расстояние между двумя точками с координатами (x1,y1) и (x2,y2). Для вычислений воспользуйтесь формулой:  .
.
12. Найдите периметр и площадь прямоугольного треугольника, если известны длины двух катетов.
13. Дана сторона равностороннего треугольника. Найти его периметр и площадь.
14. Найти площадь кольца и площадь части кольца с центральным углом j (в градусах). Для вычислений воспользоваться формулами:  ,
,  .
.
15. Найти периметр и площадь параллелограмма со сторонами a, b и углом между ними a. При вычислении использовать формулу:  .
.
16. Найти внутренний угол a и сумму внутренних углов правильного выпуклого n-угольника. При вычислении использовать формулы:  ,
,  .
.
17. Найти объем и площадь поверхности прямого параллелепипеда со сторонами a, b и c.
18. Найти среднюю линию и площадь трапеции, если известны ее основания и высота.
19. Даны координаты трех вершин треугольника A(x 1,y 1), B(x 2,y 2) и С(x 3,y3). Найти середины его сторон. При вычислении использовать формулы:  ,
,  , где M(x,y) - середина отрезка AB, заданного точками A(x 1,y 1) и B(x 2,y 2).
, где M(x,y) - середина отрезка AB, заданного точками A(x 1,y 1) и B(x 2,y 2).
20. Даны координаты трех вершин треугольника A(x 1,y 1), B(x 2,y 2) и С(x 3,y3). Вычислить периметр треугольника. Для вычислений воспользуйтесь формулой расстояния между двумя точками A(x1,y1) и B(x2,y2): 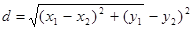 .
.
21. На плоскости дана прямая уравнением Ax+By+C=0 и точка M c координатами (x1,y1). Найти расстояние d от точки до прямой:  .
.
22. Даны два вектора 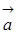 (x1,y1)и
(x1,y1)и  (x2,y2) и угол j между ними (в градусах). Найти скалярное произведение векторов по формуле:
(x2,y2) и угол j между ними (в градусах). Найти скалярное произведение векторов по формуле:  .
.
23. Даны два вектора 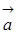 (x1,y1)и
(x1,y1)и  (x2,y2). Найти угол j между ними. При вычислении использовать формулы:
(x2,y2). Найти угол j между ними. При вычислении использовать формулы:  ,
, 
 ,
, 
 .
.
24. На плоскости даны две прямые линии: y=k1x+b1 и y=k2x+b2 . Найти угол j между прямыми, воспользовавшись формулой: 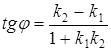 .
.
25. Вычислить углы треугольника, стороны которого заданы уравнениями прямых: y=k1x+b1, y=k2x+b2 и y=k3x+b3 . Для вычислений воспользоваться формулой: 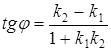 , где k1 и k2 - коэффициенты прямых, заданных уравнениями y=k1x+b1 и y=k2x+b2 , а j - угол между ними.
, где k1 и k2 - коэффициенты прямых, заданных уравнениями y=k1x+b1 и y=k2x+b2 , а j - угол между ними.
26. Написать программу для вычисления площади боковой поверхности  и объема
и объема  цилиндра по заданным радиусу основания r и высоте H. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
цилиндра по заданным радиусу основания r и высоте H. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
27. Написать программу для расчета давления газа  , где количество вещества
, где количество вещества  , по известным массе m (г) и молярной массе (г/моль) газа, температуре Т (К) и объеме V (л). Универсальную газовую постоянную R считать равной 8,31 Дж/(мольК). Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
, по известным массе m (г) и молярной массе (г/моль) газа, температуре Т (К) и объеме V (л). Универсальную газовую постоянную R считать равной 8,31 Дж/(мольК). Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
28. Написать программу для расчета времени  и дальности
и дальности  полета снаряда, вылетевшего из ствола орудия с начальной скоростью
полета снаряда, вылетевшего из ствола орудия с начальной скоростью 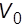 под углом к горизонту. Ускорение свободного падения
под углом к горизонту. Ускорение свободного падения 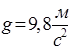 . Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
29. Написать программу, которая по заданному центральному углу и площади кругового сектора S определяет длину дуги  этого сектора, а затем рассчитывает объем конуса с длиной окружности в основании l и высотой H=2 l. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
этого сектора, а затем рассчитывает объем конуса с длиной окружности в основании l и высотой H=2 l. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
30. Написать программу для вычисления значения функции  , где
, где 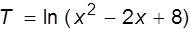 . Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
31. Написать программу для расчета ускорения свободного падения  на высоте H над поверхностью Земли. Гравитационная постоянная
на высоте H над поверхностью Земли. Гравитационная постоянная  , масса Земли
, масса Земли  , радиус Земли
, радиус Земли  . Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
32. Написать программу для расчета по заданным катету a и гипотенузе с длины второго катета прямоугольного треугольника  и угла
и угла  между a и с. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
между a и с. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
33. Написать программу для расчета плотности материала  , из которого изготовлен параллелепипед длиной a (м), шириной b (м) и высотой с (м), масса которого m (кг), а также объема
, из которого изготовлен параллелепипед длиной a (м), шириной b (м) и высотой с (м), масса которого m (кг), а также объема  образца массой 10 кг, сделанного из этого материала. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
образца массой 10 кг, сделанного из этого материала. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
34. Написать программу для вычисления значения функции  . Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
35. Написать программу для расчета скорости  электрона после прохождения им разности потенциалов U; начальная скорость электрона V0. Масса электрона
электрона после прохождения им разности потенциалов U; начальная скорость электрона V0. Масса электрона  , а заряд. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
, а заряд. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
36. Написать программу для вычисления стороны треугольника 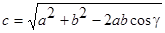 , если известны две другие его стороны a и b и угол между ними. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
, если известны две другие его стороны a и b и угол между ними. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
37. Написать программу для вычисления площади треугольника  по известным его сторонам a,b,c;
по известным его сторонам a,b,c;  - полупериметр. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
- полупериметр. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
38. Написать программу для расчета температуры газа 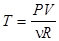 , где количество вещества
, где количество вещества  , по известным массе m (г) и молярной массе (г/моль) газа, давлении P (Па) и объеме V (л). Универсальную газовую постоянную R считать равной 8,31 Дж/(мольК). Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
, по известным массе m (г) и молярной массе (г/моль) газа, давлении P (Па) и объеме V (л). Универсальную газовую постоянную R считать равной 8,31 Дж/(мольК). Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
39. Рассчитать подъемную силу 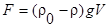 плота площадью S и толщиной D, сделанного из материала плотностью, на воде (
плота площадью S и толщиной D, сделанного из материала плотностью, на воде (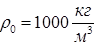 ). Объем плота V=SD, ускорение свободного падения
). Объем плота V=SD, ускорение свободного падения  . Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.


 , где g-ускорение свободного падения (9.81м/с2). Найти период колебаний маятника.
, где g-ускорение свободного падения (9.81м/с2). Найти период колебаний маятника.
 , где гравитационная постоянная g=6.673·1011м3/(кг·с2). Найти силу притяжения F.
, где гравитационная постоянная g=6.673·1011м3/(кг·с2). Найти силу притяжения F.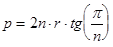 . Найти периметр р.
. Найти периметр р. , где с=2,997924·10
, где с=2,997924·10 
 -
- 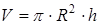 . Площадь его боковой и полной поверхностей соответственно равны:
. Площадь его боковой и полной поверхностей соответственно равны:  ,
,  . Найти V, Sб и Sn.
. Найти V, Sб и Sn. ,
,  ,
,  .
. , где d1 - диаметр шкива двигателя, d2 - диаметр рабочего вала, d3 - диаметр режущего инструмента, z - частота вращения.
, где d1 - диаметр шкива двигателя, d2 - диаметр рабочего вала, d3 - диаметр режущего инструмента, z - частота вращения. ,
,  , где Н - высота конуса, определяемая по формуле:
, где Н - высота конуса, определяемая по формуле:  .
. ,
,  , где a - центральный угол в градусах.
, где a - центральный угол в градусах. ,
,  , где a, b, c - стороны треугольника, S - площадь.
, где a, b, c - стороны треугольника, S - площадь. .
. ,
,  .
. .
. ,
,  .
. ,
,  , где M(x,y) - середина отрезка AB, заданного точками A(x 1,y 1) и B(x 2,y 2).
, где M(x,y) - середина отрезка AB, заданного точками A(x 1,y 1) и B(x 2,y 2).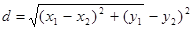 .
. .
.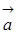 (x1,y1)и
(x1,y1)и  (x2,y2) и угол j между ними (в градусах). Найти скалярное произведение векторов по формуле:
(x2,y2) и угол j между ними (в градусах). Найти скалярное произведение векторов по формуле:  .
. ,
, 
 ,
,  .
.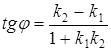 .
. и объема
и объема  цилиндра по заданным радиусу основания r и высоте H. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
цилиндра по заданным радиусу основания r и высоте H. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода. , где количество вещества
, где количество вещества  , по известным массе m (г) и молярной массе (г/моль) газа, температуре Т (К) и объеме V (л). Универсальную газовую постоянную R считать равной 8,31 Дж/(мольК). Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
, по известным массе m (г) и молярной массе (г/моль) газа, температуре Т (К) и объеме V (л). Универсальную газовую постоянную R считать равной 8,31 Дж/(мольК). Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода. и дальности
и дальности  полета снаряда, вылетевшего из ствола орудия с начальной скоростью
полета снаряда, вылетевшего из ствола орудия с начальной скоростью 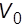 под углом к горизонту. Ускорение свободного падения
под углом к горизонту. Ускорение свободного падения 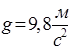 . Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода. этого сектора, а затем рассчитывает объем конуса с длиной окружности в основании l и высотой H=2 l. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
этого сектора, а затем рассчитывает объем конуса с длиной окружности в основании l и высотой H=2 l. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода. , где
, где 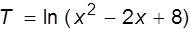 . Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода. на высоте H над поверхностью Земли. Гравитационная постоянная
на высоте H над поверхностью Земли. Гравитационная постоянная  , масса Земли
, масса Земли  , радиус Земли
, радиус Земли  . Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода. и угла
и угла  между a и с. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
между a и с. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода. , из которого изготовлен параллелепипед длиной a (м), шириной b (м) и высотой с (м), масса которого m (кг), а также объема
, из которого изготовлен параллелепипед длиной a (м), шириной b (м) и высотой с (м), масса которого m (кг), а также объема  образца массой 10 кг, сделанного из этого материала. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
образца массой 10 кг, сделанного из этого материала. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода. . Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода. электрона после прохождения им разности потенциалов U; начальная скорость электрона V0. Масса электрона
электрона после прохождения им разности потенциалов U; начальная скорость электрона V0. Масса электрона  , а заряд. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
, а заряд. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.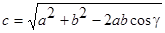 , если известны две другие его стороны a и b и угол между ними. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
, если известны две другие его стороны a и b и угол между ними. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода. по известным его сторонам a,b,c;
по известным его сторонам a,b,c;  - полупериметр. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
- полупериметр. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.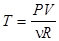 , где количество вещества
, где количество вещества  , по известным массе m (г) и молярной массе (г/моль) газа, давлении P (Па) и объеме V (л). Универсальную газовую постоянную R считать равной 8,31 Дж/(мольК). Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
, по известным массе m (г) и молярной массе (г/моль) газа, давлении P (Па) и объеме V (л). Универсальную газовую постоянную R считать равной 8,31 Дж/(мольК). Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.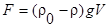 плота площадью S и толщиной D, сделанного из материала плотностью, на воде (
плота площадью S и толщиной D, сделанного из материала плотностью, на воде (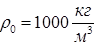 ). Объем плота V=SD, ускорение свободного падения
). Объем плота V=SD, ускорение свободного падения  . Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.
. Ответ вывести дважды: в стандартном виде и с заданной шириной поля вывода.


