РУССКОГОВОРЯЩАЯ ГРУППА!
Вихідні рівні ряду динаміки піддані сезонним змінам; для визначення загальної тенденції розвитку переходять від щомісячних рівнів до річних рівнями: 2012 - 96,7 тонн 2013 - 98,4 тонни 2014 - 101 тонна
Ці цифри, отримані в результаті переходу до річних рівнями ряду динаміки, показують загальну тенденцію зростання реалізації молочної продукції.
4.2. Метод ковзних середніх. Інший спосіб визначення тенденції у низці динаміки - метод ковзних середніх. Суть методу полягає в тому, що фактичні рівні ряду замінюються середніми рівнями, обчисленими за певним правилом, наприклад: - Вихідні або фактичні рівні ряду динаміки замінюються середніми рівнями:
У результаті виходить згладжений ряд, що складається з ковзних пятизвенная середніх рівнів. Між розташуванням рівнів і встановлюється відповідність:
— — згладжений ряд коротше вихідного на число рівнів де k - число рівнів, обраних для визначення середніх рівнів ряду. Згладжування методом ковзних середніх можна виробляти по чотирьох, п'яти або іншому числу рівнів ряду, використовуючи відповідні формули для усереднення вихідних рівнів. Отримані при цьому середні рівні називаються четирехзвенниє легкими середніми, пятизвенная легкими середніми і т.д. При згладжуванні ряду динаміки по парному числу рівнів виконується додаткова операція, звана центруванням, оскільки, при обчисленні змінного середнього, наприклад по чотирьох рівнях, відноситься до тимчасової точці між моментами часу, коли були зафіксовані фактичні рівні і. Схема обчислень і розташувань рівнів згладженого ряду стає складніше:
— — — —
Метод ковзних середніх не дозволяє отримати чисельні оцінки для вираження основної тенденції у низці динаміки, даючи лише наочне графічне представлення.
Завдання №4. Виявлення основної тенденції розвитку рядів динаміки методом укрупнення інтервалів і ковзаючих середніх. Умова задачі: Є такі дані про реалізацію молочної продукції в магазинах міста по місяцях із 2004 - 2007 р.р. (тис.т.), представлені на рис.4.
Для вивчення загальної тенденції реалізації даної продукції необхідно: 1. Провести перетворення вихідних даних шляхом укрупнення періодів часу: а) у квартальні рівні, б) в річні рівні; 2. Побудувати лінійний графік квартальних рівнів; 3. Провести згладжування квартальних рівнів із застосуванням пятизвенная ковзної середньої; 4. Побудувати графік пятизвенная ковзної середньої. 5. Зробити висновки про характер основної тенденції досліджуваного явища.
Хід виконання: 1. У книгу Ряди дінамікі.xls додайте новий лист і перейменуйте його в лист Завдання 4. 2. Створіть таблицю згідно рис.4.
Рис.4. Дані для завдання №4.
3. Проведіть перетворення вихідних даних шляхом укрупнення періодів часу в річні рівні, розрахувавши обсяги продажів за 2004-2007 р.р. у відповідних осередках. 4. Проведіть перетворення вихідних даних шляхом укрупнення періодів часу в квартальні рівні, розрахувавши обсяги продажів по кварталах за 2004-2007 р.р. у відповідних осередках. 5. Побудуйте ряд динаміки квартальних рівнів в діапазоні осередків А18: С34 згідно рис. 5, додавши в стовпець З розраховані квартальні обсяги продажів.
Рис.5. Ряд динаміки (по кварталах) 6. На підставі квартальних рівнів побудуйте діаграму (тип - графік), яка відображатиме ряд динаміки. 7. Проведіть згладжування квартальних рівнів із застосуванням пятизвенная ковзної середньої, використовуючи функцію СРЗНАЧ в діапазоні осередків D19: D34. 8. Проведіть згладжування квартальних рівнів із застосуванням пятизвенная ковзної середньої, використовуючи інструмент аналізу ковзної середньої. Для цього: • Виконайте команду Сервіс / Аналіз даних. • Виберіть інструмент Ковзаюче середнє. • У діалоговому вікні встановіть параметри згідно рис. 6.
Рис. 6. Діалогове вікно «Ковзаюче середнє».
9. Побудуйте графік пятизвенная ковзної середньої, додавши новий ряд на вже існуючий графік (див. Рис.7).
Рис.7. Графіки ряду динаміки і ковзної середньої.
10. Зробіть висновок про характер основної тенденції розвитку досліджуваного явища. 11. Збережіть зміни в книзі Ряди дінамікі.xls.
4.3. Метод аналітичного вирівнювання. Застосування в аналізі рядів динаміки методів укрупнення інтервалів і ковзної середньої дозволяє виявити тренд (тенденцію) для його опису, але отримати узагальнену статистичну оцінку тренду за допомогою цих методів неможливо. Вирішення цієї більш високого порядку завдання - вимірювання тренда - досягається методом аналітичного вирівнювання. Основним змістом методу аналітичного вирівнювання в рядах динаміки є те, що основна тенденція розвитку розраховується як функція часу ŷt = ƒ (ti) (4.4) Визначення теоретичних (розрахункових) рівнів ŷt виробляється на основі так званої адекватної математичної функції, яка найкращим чином відображає основну тенденцію ряду динаміки. Підбір адекватної функції здійснюється методом найменших квадратів, сутність якого полягає в мінімізації суми квадратів відхилень між емпіричними yi і теоретичними ŷt рівнями: (Yi - ŷt) 2 = min (4.5) Найважливішою проблемою, яка потребує свого рішення при застосуванні методу аналітичного вирівнювання, є підбір математичної функції, за якою розраховуються теоретичні рівні тренду. Від правильності вирішення цієї проблеми залежать висновки про закономірності тренду досліджуваних явищ. Якщо вибраний тип математичної функції адекватний основній тенденції розвитку досліджуваного явища в часі, то синтезована на його основі трендова модель може мати корисне застосування при вивченні сезонних коливань, прогнозуванні та інших практичних цілях. Однією з умов обгрунтованого застосування методу аналітичного вирівнювання в аналізі рядів динаміки є знання типів розвитку соціально-економічних явища в часі, їх основних відмінних ознак. У практиці статистичного вивчення тренда розрізняють наступні еталонні типи розвитку соціально-економічних явищ у часі. 1. Рівномірний розвиток. Для цього типу розвитку притаманні постійні ланцюгові абсолютні прирости:
Основна тенденція розвитку в рядах динаміки зі стабільними абсолютними приростами відображається рівнянням прямолінійною функції.
де a0 і a1 - параметри рівняння; t - час. Параметр a0 є коефіцієнтом регресії, визначальним напрям розвитку. Якщо a1> 0, то рівні ряду динаміки рівномірно зростають, а при a1 <0 відбувається їх рівномірне зниження. Якщо у формулі (4.5) замість ŷt підставити, то отримаємо:
Це функція двох змінних (все і невідомі), яка за певних досягає мінімуму. З цього виразу на основі знань, отриманих в курсі вищої математики про екстремумі функцій n змінних, отримують значення коефіцієнтів.
де n - число моментів часу, для яких були отримані вихідні рівні ряду. Якщо замість абсолютного часу вибрати умовний час таким чином, щоб
2. Рівноприскорений (равнозамедленно) розвиток. Цьому типу динаміки властиво постійне в часі збільшення (уповільнення) розвитку. Рівні таких рядів динаміки змінюються з постійними ланцюговими темпами приросту:
Основна тенденція розвитку в рядах динаміки зі стабільними темпами приросту відображається функцією параболи другого порядку:
У формулі (4.9) параметри a0 і a1 ідентичні параметрам, використовуваним у формулі (4.7). Параметр a2 характеризує постійна зміна інтенсивності розвитку (в одиницю часу). Якщо a2> 0, то відбувається прискорений розвиток, а при a2 <0 йде процес уповільнення зростання. 3. Розвиток зі змінним прискоренням (уповільненням). Для цього типу динаміки основна тенденція розвитку відображається функцією параболи третього порядку:
У формулі (4.10) параметр a3 відображає зміну прискорення. Якщо a3> 0, то прискорення зростає, при a3 <0 прискорення сповільнюється. 4. Розвиток по експоненті. Цей тип динаміки характеризує стабільні ланцюгові темпи зростання:
Основна тенденція розвитку в рядах динаміки з постійними темпами зростання відображається показовою функцією:
де a1 - темп зростання (зниження) досліджуваного явища в одиницю часу, тобто інтенсивність розвитку.
5. Розвиток з уповільненням зростання в кінці періоду. У цього типу динаміки показання ланцюгового абсолютного приросту скорочується в кінцевих рівнях ряду динаміки:
Основна тенденція розвитку в таких рядах динаміки відображається полулогарифмической функцією:
При аналітичному вирівнюванні в рядах динаміки можна застосовувати й інші математичні функції. Так, при вивченні основної тенденції розвитку незадоволеного та реалізованого попиту населення застосовуються Степенева функція: Функція гіперболи:
Завдання №5. Аналіз основної тенденції розвитку ряду динаміки методом аналітичного вирівнювання. Умова задачі. За даними про кількість населення м Мінська (див. Рис. 8) провести аналіз основної тенденції розвитку міста.
Хід виконання: 1. У книгу Ряди дінамікі.xls додайте новий лист і перейменуйте його в лист Завдання 5. 2. Створіть таблицю згідно рис.8. 3. Розрахуйте темпи зростання населення м Мінська і абсолютний приріст за часовий період 1991-2001 р.р. ланцюговим методом 4. Розрахуйте середній рівень ряду динаміки, середній темп зростання і середній абсолютний приріст в осередках B14, C14, D14 відповідно.
Рис.8. Дані про чисельність населення.
5. Для аналітичного вирівнювання в даному випадку будемо застосовувати функцію, що відповідає рівномірному розвитку. 6. Для знаходження коефіцієнтів a0 і a1, а також теоретичних рівнів тренду, побудуйте матрицю розрахункових показників згідно рис. 9 (додайте в книгу новий лист і надайте йому ім'я Трендовая модель).
Рис.9. Матриця розрахункових показників.
7. Оскільки формули (4.11 і 4.12) для розрахунку коефіцієнтів a0 і a1 отримані при, то поступають таким чином: рівень, що стоїть в середині ряду (1996 г.) приймається за умовний початок відліку, тоді дати, які стоять вище цього рівня, позначаються натуральними числами зі знаком «мінус», а нижче - зі знаком «плюс». 8. Розрахуйте моменти часу в стовпці D і твір рівнів ряду динаміки yi на моменти часу ti в стовпці Е. 9. У рядку Разом розрахуйте,,,. 10. В осередках А21 і B21 розрахуйте коефіцієнти рівняння a1 і a0 за формулами 4.12 і 4.11. 11. Перевірте правильність розрахунків за допомогою функції ЛИНЕЙН в осередках А23 і B23. 12. Порівняйте отримані результати з рис. 10.
Рис.10. Коефіцієнти рівняння.
13. Запишіть отримане рівняння прямолінійної функції в комірці А25. 14. Параметр a1 показує, що чисельність населення м Мінська в 1991-2001 р.р. зросла в середньому на 4510 осіб рік. 1. 15. На основі отриманої моделі знайдіть теоретичні рівні ряду динаміки. Для цього в комірці F3 запишіть формулу 16. Розрахуйте решта теоретичні рівні ряду динаміки в стовпці F. 17. Розрахуйте суму теоретичних рівнів ряду динаміки в комірці F14, порівняйте отриманий результат із сумою емпіричних рівнів. 18. Побудуйте в одних координатних осях графіки емпіричних рівнів і теоретичних рівнів ряду динаміки. 19. Додайте лінію тренда для графіка емпіричних рівнів, встановіть прапорець «Показати рівняння на діаграмі». 20. Проаналізуйте отримані результати і зробіть висновки.
5. Прогнозування в рядах динаміки. Обумовлені в аналізі рядів динаміки показники зміни рівнів, тренда мають широке застосування при прогнозуванні, тобто при отриманні статистичної оцінки можливого заходу розвитку соціально-економічних явищ на майбутнє. Важливе значення при цьому мають статистичні методи екстраполяції та прогнозування. Під екстраполяцією розуміється поширення виявлених в аналізі рядів динаміки закономірностей розвитку досліджуваного явища на майбутнє. Більш широке поняття являє собою прогнозування, основою якого є припущення, що закономірність, діюча всередині аналізованого ряду динаміки, що виступає в якості бази прогнозування, зберігається і надалі. Точність прогнозу залежить від того, наскільки обгрунтованими виявляться припущення про збереження на майбутнє дій тих чинників, які сформували у базисному ряду динаміки його основні компоненти. Важливе значення при екстраполяції має тривалість ряду динаміки і термінів прогнозування. При екстраполяції динаміки соціально-економічних явищ слід брати ті субперіоду базисного ряду динаміки, які складають певний етап у розвитку досліджуваного явища. Встановлення термінів прогнозування залежить від завдання дослідження. Слід мати на увазі, що чим коротше терміни попередження прогнозу, тим надійніше результати. Застосування методів екстраполяції залежить від характеру змін в базисному ряду динаміки і зумовлюється завданням дослідження. 1. Лінійні прогнози. При екстраполяції рівнів розвитку досліджуваного явища на базі ряду динаміки з постійними абсолютними приростами () застосовується формула:
де -
-
Для побудови лінійних прогнозів MS Excel використовується статистична функція ТЕНДЕНЦІЯ, яка повертає значення відповідно до лінійною апроксимацією за методом найменших квадратів. Для побудови лінійних прогнозів MS Excel використовується статистична функція ТЕНДЕНЦІЯ, яка повертає значення відповідно до лінійною апроксимацією за методом найменших квадратів. 2. Нелінійні прогнози. При екстраполяції рівня розвитку досліджуваного явища на базі ряду динаміки зі стабільними ланцюговими темпами зростання () застосовується формула:
Для побудови нелінійних прогнозів MS Excel використовується статистична функція РОСТ, яка розраховує прогнозований експоненціальне зростання на підставі наявних даних. При прогнозуванні тенденції досліджуваного явища на основі аналітичного вирівнювання для екстраполяції тренда застосовуються адекватні трендові моделі. При складанні прогнозів використовують интервальную оцінку. Величина довірчого
де
Де n - число рівнів ряду; m - кількість параметрів в рівнянні ряду (для прямолінійного функції m = 2).
n - m = v - число ступенів свободи.
Завдання №5. Лінійні прогнози рядів динаміки. Умова задачі. За даними про кількість населення м Мінська на 1991-2001 р.р необхідно спрогнозувати чисельність населення на 2002 рік.
Хід виконання:
1. Скопіюйте дані про чисельність населення м Мінська з аркуша Завдання 5 на новий аркуш і надайте йому ім'я Лінійний прогноз. 2. Додайте фрагмент книги згідно рис. 11.
Рис.11. 3. 1-й спосіб (за формулою). Визначте в комірці С16 за формулою (5.1) можливу чисельність населення м Мінська в 2002 р, враховуючи, що розрахований середній абсолютний приріст 4. 2-й спосіб (на основі трендової моделі). Використовуючи рівняння отриманої трендової моделі (див. Дані листа Трендовая модель), зробіть прогноз населення м Мінська на 2002 рік в комірці С17. Для цього знайдіть значення теоретичного рівня 5. третій спосіб (з використанням функції ТЕНДЕНЦІЯ). Зробіть прогноз населення м Мінська в 2002 р в комірці С18, використовуючи статистичну функцію ТЕНДЕНЦІЯ. Для цього: • Встановіть курсор в осередок С18. • Викличте функцію ТЕНДЕНЦІЯ (категорія Статистичні). • У діалоговому вікні встановіть параметри згідно рис. 12.
Рис.12. Вікно функції ТЕНДЕНЦІЯ.
де Ізвестние_значенія_у - це масив відомих значень рівнів ряду динаміки, які описуються лінійної трендової моделлю Ізвестние_значенія_х - відомі періоди часу (необов'язковий параметр). Новие_значенія_х - період часу, на який розраховується прогноз.
6. Порівняйте отримані результати з рис. 13.
Рис.13. Прогноз на 2002 рік. 7. 4-й спосіб (графічний). На аркуші Трендовая модель для лінії тренду на вкладці Параметри встановіть опцію «Прогноз» на один період вперед. 8. Проаналізуйте отримані результати. 9. Знайдіть довірчий інтервал, в межах якого знаходиться. Для цього: • На аркуші Трендовая модель розрахуйте • В осередку Н14 знайдіть суму квадратів відхилень емпіричних і розрахункових значень ряду динаміки. • В осередку Н16 за формулою (5.4) розрахуйте середнє квадратичне відхилення • Враховуючи, що для заданих довірчої ймовірності 10. Визначте, чи входить прогнозоване значення, розраховане за формулою (5.1), в отриманий довірчий інтервал.
Завдання №6. Нелінійні прогнози рядів динаміки. 1. Для дослідження можливостей прогнозування у разі нелінійної залежності на новому аркуші Нелінійний прогноз введіть дані стовпців А (Тиждень) і В (Замовлення) згідно рис. 14.
Рис.14. Дані для нелінійного прогнозу. 2. Для побудови прогнозу на період 11-13, скористайтеся статистичної функцією РОСТ. Для цього: • Виділіть діапазон комірок С2: С14. • Викличте функцію РОСТ (категорія Статистичні). • У діалоговому вікні встановіть параметри згідно рис. 15. • Натисніть комбінацію клавіш SHIFT + CTRL + ENTER.
де Ізвестние_значенія_у - це масив відомих значень рівнів ряду динаміки, які описуються експоненціальною трендової моделлю зі стабільними темпами зростання ( Ізвестние_значенія_х - відомі періоди часу (необов'язковий параметр). Новие_значенія_х - періоди часу, на які робиться прогноз.
3. Побудуйте графік для досліджуваного ряду динаміки. На графік додайте лінію тренда (тип тренда - експонентний). На вкладці «Параметри» встановіть прапорець «Показати рівняння на діаграмі», вкажіть «Прогноз» на три періоди вперед. 4. Додайте на графік ряд на основі функції РОСТ. 5. Порівняйте прогноз, отриманий графічним способом і розрахований за допомогою функції РОСТ, і зробіть висновки.
РУССКОГОВОРЯЩАЯ ГРУППА!
|

 (4.1)
(4.1) (4.2)
(4.2)
 (4.3)
(4.3)
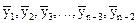 — —,
— —, ,
, ... - Вихідні рівні;
... - Вихідні рівні;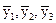 ... - Згладжені рівні;
... - Згладжені рівні;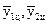 ... - Центровані згладжені рівні;
... - Центровані згладжені рівні;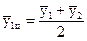
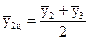 .
.



 (4.6)
(4.6) (4.7)
(4.7) (4.8)
(4.8)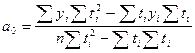 (4.9)
(4.9) (4.10)
(4.10) , то записані вирази для визначення спрощуються:
, то записані вирази для визначення спрощуються: (4.11) і
(4.11) і  (4.12)
(4.12) (4.13)
(4.13)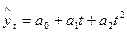 (4.14)
(4.14) (4.15)
(4.15) (4.16)
(4.16) (4.17)
(4.17) (4.18)
(4.18) (4.19)
(4.19) (4.20)
(4.20) (4.21)
(4.21)


 для розрахунку.
для розрахунку.  .
. (5.1)
(5.1) - екстраполіруемий рівень,
- екстраполіруемий рівень, - Кінцевий рівень базисного ряду динаміки
- Кінцевий рівень базисного ряду динаміки - Термін прогнозу.
- Термін прогнозу.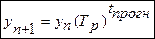 (5.2)
(5.2)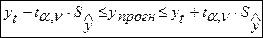 (5.3)
(5.3) - значення t-критерію Стьюдента для заданої довірчої ймовірності
- значення t-критерію Стьюдента для заданої довірчої ймовірності  і числа ступенів свободи
і числа ступенів свободи  ;;
;; - Середнє квадратичне відхилення від тренду, що визначається за формулою:
- Середнє квадратичне відхилення від тренду, що визначається за формулою: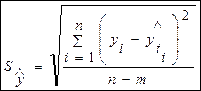 (5.4)
(5.4) і
і  - відповідно емпіричне і розрахункове значення рівнів ряду;
- відповідно емпіричне і розрахункове значення рівнів ряду;
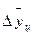 = 5,5 тис.чол.
= 5,5 тис.чол. при t = 6.
при t = 6.
 .
.
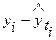 і
і  в осередках G3: G13 і осередках Н3: Н13 відповідно.
в осередках G3: G13 і осередках Н3: Н13 відповідно.
 ,, враховуючи, що число рівнів ряду динаміки n = 11, а число параметрів прямолінійного рівняння m = 2.
,, враховуючи, що число рівнів ряду динаміки n = 11, а число параметрів прямолінійного рівняння m = 2. значення t-критерію Стьюдента
значення t-критерію Стьюдента  , за формулою (5.3) знайдіть довірчий інтервал, в межах якого лежить прогнозоване значення
, за формулою (5.3) знайдіть довірчий інтервал, в межах якого лежить прогнозоване значення  .
.




