Основные цели и задачи.
Лабораторные работы № 4
М и н с к 2 0 1 2
Основные цели и задачи. изучить закон сохранения и превращения механической энергии при движении тел в поле консервативных сил; изучить закон сохранения импульса; экспериментально проверить выполнение этих законов. Движение центра инерции. Закон сохранения импульса.
Рассмотрим движение произвольной системы материальных точек (частиц). Пусть О – начало системы координат, а mi, r i и v i – масса, радиус-вектор и скорость i – ой частицы (рис. 1). Центром инерции или центром масс системы материальных точек называют такую точку С, радиус-вектор которой
где Скорость центра инерции системы:
где р – импульс всей системы. Таким образом,
т.е. импульс системы равен произведению массы всей системы на скорость ее центра инерции. Силы, действующие на систему материальных точек со стороны тел, не входящих в данную систему (внешних тел), называют внешними силами. Силы взаимодействия между частицами данной системы называют внутренними силами. Пусть F iвнешн – результирующая всех внешних сил, действующих на i -ю частицу, а F ik – сила, действующая на нее со стороны k -ой частицы системы (рис. 5). Напишем уравнения движения для каждой частицы системы:
Если сложить все уравнения почленно и учесть, что
и, то в результате получим:
Это уравнение является обобщением 2-го закона Ньютона на произвольную механическую систему. С учетом (2) можно записать:
где а с – ускорение центра инерции. Таким образом,
Формула (5) выражает закон сохранения импульса: импульс механической системы не изменяется с течением времени, если сумма всех внешних сил, действующих на систему, равна нулю. В частности, импульс сохраняется у замкнутой системы тел, т.е. системы, на которую не действуют внешние силы. Спроецируем уравнение (3) на некоторую координатную ось, например, Ох: Если Таким образом, в случае незамкнутой системы, если сумма проекций внешних сил на какую-либо ось равна нулю, то проекция на эту же ось вектора импульса сохраняется. Это утверждение называют законом сохранения проекции импульса.
Кинетическая энергия. Работа.
Умножим уравнение движение материальной точки
Учтем, что Если на материальную точку сила не действует (
Под действием силы F кинетическая энергия частицы изменяется, и в соответствии с формулой (6) ее приращение равно F· d r. Величина dA = F· d r называется элементарной работой, совершаемой силой F при перемещении частицы на d r (рис.3). Так как F· d r = F·| d r |· cos α, то элементарную работу можно выразить через проекцию силы на направление перемещения Fs =F cos α и приращение пути ds, равно модулю элементарного перемещения:
Отметим, что в зависимости от угла между направлениями перемещения и силы, последняя может выполнять как положительную (0 ≤ α < π/2, приращение кинетической энергии частицы положительно), так и отрицательную работу (π/2 < α ≤ π, приращение кинетической энергии частицы отрицательно, работа выполняется против силы за счет запаса кинетической энергии частицы). В частности, при α = π/2 работа не выполняется и кинетическая энергия сохраняется. При движении частицы по конечному участку траектории от точки 1 до точки 2 (рис. 3) полную работу найдем как сумму работ на отдельных элементарных участках, т.е. как интеграл по траектории от точки 1 до точки 2:
Учитывая (6) и (7), находим:
Таким образом, работа сил, действующих на частицу, равна приращению кинетической энергии частицы. В СИ единицей работы и энергии является джоуль: 1 Дж = 1 Н · м.
Потенциальное поле. Потенциальная энергия. Консервативные силы.
Если частица в каждой точке пространства подвержена действию сил, то говорят, что она находится в поле сил. Например, вблизи поверхности Земли в каждой точке пространства на частицу действует сила тяжести G = m g. Поэтому говорят, что частица находится в поле силы тяжести. Пусть в некоторой декартовой системе координат под действием силы F = Fx i + Fy j + Fz k частица совершает элементарное перемещение d r = dx i + dy j + dz k. Если стационарное силовое поле можно описать с помощью функции U(x, y, z) такой, что
то такое поле называется потенциальным, а функция U(x, y, z) есть потенциальная энергия тела, на которое действует силовое поле, создаваемое другими телами в данной точке пространства. Таким образом, потенциальная энергия – механическая энергия системы тел, определяемая характером взаимодействия между телами и их взаимным расположением. Для потенциального поля
Элементарная работа сил поля
где dU − полный дифференциал функции U(x, y, z). Если частица переместилась из точки 1 в точку 2, потенциальная энергия в которых равна U1 и U2 соответственно, то полная работа сил поля (рис. 7):
Силы, работа которых не зависит от формы траектории, по которой частица перемещается из одного положения в другое, называются консервативными. Поле консервативных сил является потенциальным полем. Легко видеть, что работа консервативных сил при перемещении частицы по замкнутой траектории равна нулю. Для доказательства этого достаточно положить в (9), что частица, пройдя некоторый путь, возвратилась в исходное положение (т.е., что точки 1 и 2 совпадают). Понятие потенциальной энергии можно ввести только для полей консервативных сил. Согласно формуле (9), потенциальная энергия численно равна работе, совершаемой консервативными силами поля при перемещении частицы из данной точки в точку, потенциальная энергия в которой принята за нуль (в зависимости от конкретной задачи). Силы, работа которых зависит от формы траектории и относительной скорости, называются диссипативными. Примером консервативной силы является сила тяжести. Работа силы тяжести A = mg (h 1 – h 2), где h 1 и h 2 – начальная и конечная высота тела над поверхностью Земли, не зависит от формы пути. Теми же свойствами обладают силы упругости при не слишком больших деформациях. Напротив, силы трения – диссипативные силы.
Закон сохранения механической энергии.
Сравнивая выражения (8) и (9) для работы, выполненной консервативными силами по перемещению материальной точки, можно записать
или после переноса
Последний результат означает, что величина E = E к + U для частицы, находящейся в поле консервативных сил, остается постоянной, т.е.
Величину Е, т.е. сумму кинетической и потенциальной энергии, называют полной механической энергией частицы. Формулу (12) можно распространить на систему невзаимодействующих между собой материальных точек, находящихся в поле консервативных сил. Полная механическая энергия такой системы сохраняется
Здесь Ui – потенциальная энергия i –ой частицы в поле внешних консервативных сил. Теперь учтем взаимодействие между частицами системы. В этом случае в полную энергию системы дает вклад потенциальная энергия взаимодействия частиц между собой. Эта энергия зависит от взаимного расстояния для каждой пары частиц, т.е. в конечном итоге от конфигурации системы в целом.
где
Полная механическая энергия системы взаимодействующих тел, при действии только консервативных сил (как внешних, так и внутренних), остается постоянной. Это и есть закон сохранения полной механической энергии.
ЧАСТЬ А. Экспериментальная проверка выполнения закона сохранения механической энергии.
МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ
Рассмотрим работу установки. Через блок, вращающийся с малым трением, перекинута нить, на концах которой подвешены грузы m 0и m. Масса груза m больше, чем m 0, и его устанавливают на высоте h над нулевой отметкой (уровень нижнего фотодатчика 2). При этом длина нити должна быть такой, чтобы груз m 0находился не выше нулевой отметки (в противном случае этот груз достигнет блока раньше, чем груз m опустится на нулевую отметку). При разблокировании системы она приходит в движение, груз m опускается в конце пути на нулевую отметку, а груз m 0при этом поднимается на высоту h, так как нить практически не растяжима. Потенциальная энергия mgh, которой обладал груз m в исходном состоянии, превращается в его кинетическую энергию, а также в кинетическую и потенциальную энергию груза m 0. Кроме того часть энергии расходуется на совершение работы против сил трения на оси блока и сил сопротивления воздуха. Таким образом, закон сохранения и превращения энергии в данном случае принимает вид:
Момент инерции блока можно считать как момент инерции диска:
В работе используются грузы одинаковой формы, поэтому на них действуют равные силы сопротивления воздуха. Груз набирается из основы массой m 0 = (21,50 ± 0,05) г и дополнительных шайб с прорезями для надевания на основу, масса каждой из них m ' = (5,50 ± 0,05) г. Таким образом можно набрать массы m 1 = m 0+ m ' = (27,00 ± 0,10) г, m 2 = m 0+ 2 m ' = (32,50 ± 0,15) г. Для двух различных правых грузов с массами m 1и m 2 в соответствии с (46) получим два независимых уравнения
Учитывая, что работы против сил трения и сопротивления среды при различных значениях массы правого груза практически равны, из системы уравнений (19) получим:
Используя выражения (47), (48), (49), получим окончательную рабочую формулу:
Измерив значения величин h, t 1, t 2, и используя приведенные выше значения m 1, m 2, m 0, М и
Задание: 1. Провести измерение величин h, t 1, t 2, входящих в формулу (21). Времена t 1 и t 2 определить по серии из 5 измерений для каждого, определить абсолютные случайные погрешности измерения времени Δ t 1 и Δ t 2. 2. Подставить измеренные величины в формулу и провести вычисления. 3. Рассчитать погрешности выражений, стоящих в левой и правой части равенства (21). 4. Сравнить численные значения правой и левой частей и сделать вывод о выполнении закона сохранения энергии в механике.
МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ
Наиболее отчетливо закон сохранения импульса проявляется при соударении двух тел. Удар – это кратковременное взаимодействие тел, двигавшихся до этого с различными скоростями, при их соприкосновении, в результате которого резко меняется состояние их движения. При этом считается, что как до, так и после удара тела не взаимодействуют. Прямая, совпадающая с нормалью к поверхности соударяющихся тел в точке их соприкосновения, называется линией удара. Если линия удара проходит через центры масс тел, удар называется центральным. Если оба соударяющихся тела до удара двигались по линии удара, то удар называется прямым, в противном случае удар будет косым. Прямой центральный удар является абсолютно неупругим, если скорости тел после соударения становятся одинаковыми, так что оба тела движутся вместе, оставаясь в соприкосновении и в деформированном состоянии. Пусть два шара, массы которых m 1 и m 2 , до удара двигались со скоростями v 1 и v 2. После абсолютно неупругого удара они будут двигаться с общей скоростью u. Так как силы взаимодействия между шарами при ударе являются внутренними, то они не могут изменить общего импульса системы шаров. Значит:
Из этого выражения видно, что после удара оба шара будут двигаться в сторону движения шара, обладавшего до удара большим импульсом. Суммарная кинетическая энергия шаров после неупругого удара становится меньше, чем до удара, поскольку часть ее расходуется на создание деформаций, не исчезающих после удара, и превращается в конечном итоге в энергию молекулярно-теплового движения. Таким образом, кинетическая энергия шаров после удара Суммарная кинетическая энергия шаров до удара равна
после удара
Следовательно, работа деформации в процессе удара равна
Вторым крайним случаем прямого центрального удара является абсолютно упругий удар. Удар называется абсолютно упругим, если суммарные кинетические энергии соударяющихся тел после удара и до удара равны. После упругого удара скорости соударяющихся тел u 1 и u 2 различны, а сами тела не деформированы. Запишем для прямого, центрального, абсолютно упругого удара двух шаров законы сохранения импульса и механической энергии:
 . (26) Решив эту систему уравнений, получим скорости шаров после удара . (26) Решив эту систему уравнений, получим скорости шаров после удара
Пусть два шара подвешены на практически нерастяжимых нитях. Массы шаров m 1 и m 2, диаметры одинаковы (рис. 6). Если шар 2 отвести на угол α от положения равновесия и отпустить, то между шарами произойдет упругий удар. До соударения шар 1 покоится в состоянии равновесия, т.е. v 1 = 0. В момент соударения шары образуют замкнутую систему, так как в положении, в котором происходит удар, внешние силы, приложенные к шарам, уравновешивают друг друга. Следовательно, по закону сохранения импульса:
Скорость шара 2 v 2 в момент, предшествующий удару, определяется из закона сохранения энергии. Шар, отклоненный на угол α, обладает потенциальной энергией Eп = mgh. В положении равновесия эта энергия переходит в кинетическую энергию
Тогда проверка выполнения закона сохранения импульса заключается в проверке выполнения равенства
Задание: 1. Измерьте углы отклонения шаров α, α1 и α2. Определите погрешность их измерения. 2. По формуле (32) проверьте выполнение закона сохранения импульса. Контрольные вопросы к лабораторной работе № 4 1. Чему равна работа силы? Как определить работу переменной силы? 2. Назовите виды механической энергии. 3. Сформулируйте закон сохранения механической энергии. 4. Дайте определение импульса тела. 5. Сформулируйте закон сохранения импульса. 6. Что собой представляет абсолютно упругий удар? Что собой представляет абсолютно неупругий удар? 7. Как на опыте осуществляется проверка закона сохранения механической энергии? Сделайте вывод расчетной формулы. 8. Как на опыте осуществляется проверка закона сохранения импульса? Какие при этом проводятся прямые измерения?
Литература
1. Трофимова Т.И. Курс физики: Учеб. пособие для вузов. М.: Высш. шк., 2003. -541 с. 2. Савельев И.В. Курс общей физики. Учеб. пособие. В 3-х т. Т.1 Механика. Молекулярная физика. М.: Наука. Гл.ред. физ.мат. лит., 1987. – 432 с. 3. Петровский И.И. Механика. Мн.: Изд-во Белорус. ун-та, 1973.– 352 с. 4. Сивухин Д.В. Механика: Учеб. пособие для вузов. М.: Наука. Гл.ред. физ.мат. лит., 1989. – 576 с. – (Общий курс физики; Т. I)
|


 ,(1)
,(1) − масса всей системы.
− масса всей системы. ,
, ,(2)
,(2)



 .(3)
.(3)
 , (4) т.е. движение центра инерции системы не зависит от внутренних сил, действующих между телами данной системы, а определяется лишь внешними силами. Если результирующая всех внешних сил, приложенных к системе, равна нулю, то
, (4) т.е. движение центра инерции системы не зависит от внутренних сил, действующих между телами данной системы, а определяется лишь внешними силами. Если результирующая всех внешних сил, приложенных к системе, равна нулю, то и
и  . (5)
. (5) .
. , то
, то  , откуда
, откуда 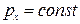 .
. на элементарное перемещение
на элементарное перемещение  . Тогда
. Тогда .
. , а
, а  . Окончательно получим
. Окончательно получим  . (6)
. (6) = 0), то
= 0), то 
 и
и  .
. Величину Eк называют кинетической энергией. Кинетическая энергия тела – энергия, обусловленная его механическим движением. Она численно равна работе, которую необходимо совершить, чтобы сообщить телу массы m скорость v. Смысл введения кинетической энергии состоит в том, что это – сохраняющаяся величина при движении материальной точки в отсутствие действия сил. Кинетическая энергия – величина аддитивная, для системы из n материальных точек она равна сумме кинетических энергий отдельных точек:
Величину Eк называют кинетической энергией. Кинетическая энергия тела – энергия, обусловленная его механическим движением. Она численно равна работе, которую необходимо совершить, чтобы сообщить телу массы m скорость v. Смысл введения кинетической энергии состоит в том, что это – сохраняющаяся величина при движении материальной точки в отсутствие действия сил. Кинетическая энергия – величина аддитивная, для системы из n материальных точек она равна сумме кинетических энергий отдельных точек:

 .
. . (7)
. (7) .
. . (8)
. (8)
 ,
, .
. ,
, , (9) т.е. работа, совершаемая над частицей, равна убыли ее потенциальной энергии. Форма траектории, по которой двигалась частица, может быть совершенно произвольной. В любом случае изменение потенциальной энергии будет одним и тем же. Таким образом, работа, совершаемая над частицей силами потенциального поля, не зависит от формы траектории, а определяется только начальным и конечным положениями частицы.
, (9) т.е. работа, совершаемая над частицей, равна убыли ее потенциальной энергии. Форма траектории, по которой двигалась частица, может быть совершенно произвольной. В любом случае изменение потенциальной энергии будет одним и тем же. Таким образом, работа, совершаемая над частицей силами потенциального поля, не зависит от формы траектории, а определяется только начальным и конечным положениями частицы. (10)
(10) . (11)
. (11)
 . (12)
. (12) . (13)
. (13) , (14)
, (14) – потенциальная энергия системы во внешнем поле,
– потенциальная энергия системы во внешнем поле, − потенциальная энергия взаимодействия частиц.
− потенциальная энергия взаимодействия частиц.
 Схема экспериментальной установки представлена на рис. 5. Как видно из рисунка, установка для проверки закона сохранения механической энергии имеет ту же базовую часть, что и машина Атвуда в лабораторной работе № 7. Поэтому для более полного ознакомления с установкой можно также изучить описание установки к работе № 7, приведенное в этом же методическом пособии. Основное отличие заключается в отсутствии устройства для съема перегрузка, весь путь система грузов проходит равноускоренно. Электронный секундомер автоматически запускается в момент начала движения системы импульсом с фотореле 1, формируемым при пересечении правым грузом светового луча в нем, и таким же образом останавливается при помощи фотореле 2, установленного в нижней точке пути. Таким образом, высота h, фигурирующая в выводимой ниже рабочей формуле, есть расстояние между уровнями фотодатчиков 1 и 2, измеряемое по линейке на колонне. Поскольку рабочая формула справедлива только при начальной кинетической энергии системы, равной нулю, то при проведении измерений очень важно в исходном состоянии устанавливать нижний срез правого груза m точно по уровню верхнего фотодатчика 1. Блок затормаживается электромагнитом при отжатой кнопке «Пуск» на электронном приборе и система удерживается в статическом состоянии (блокируется). Блокировка снимается нажатием кнопки «Пуск», при этом кнопка фиксируется в нажатом положении. При проведении очередного замера времени необходимо обнулить предыдущее показание секундомера с помощью кнопки «Сброс».
Схема экспериментальной установки представлена на рис. 5. Как видно из рисунка, установка для проверки закона сохранения механической энергии имеет ту же базовую часть, что и машина Атвуда в лабораторной работе № 7. Поэтому для более полного ознакомления с установкой можно также изучить описание установки к работе № 7, приведенное в этом же методическом пособии. Основное отличие заключается в отсутствии устройства для съема перегрузка, весь путь система грузов проходит равноускоренно. Электронный секундомер автоматически запускается в момент начала движения системы импульсом с фотореле 1, формируемым при пересечении правым грузом светового луча в нем, и таким же образом останавливается при помощи фотореле 2, установленного в нижней точке пути. Таким образом, высота h, фигурирующая в выводимой ниже рабочей формуле, есть расстояние между уровнями фотодатчиков 1 и 2, измеряемое по линейке на колонне. Поскольку рабочая формула справедлива только при начальной кинетической энергии системы, равной нулю, то при проведении измерений очень важно в исходном состоянии устанавливать нижний срез правого груза m точно по уровню верхнего фотодатчика 1. Блок затормаживается электромагнитом при отжатой кнопке «Пуск» на электронном приборе и система удерживается в статическом состоянии (блокируется). Блокировка снимается нажатием кнопки «Пуск», при этом кнопка фиксируется в нажатом положении. При проведении очередного замера времени необходимо обнулить предыдущее показание секундомера с помощью кнопки «Сброс». , (15) где v – конечная скорость груза (его скорость на нулевой отметке); ω; и I – соответственно, конечная угловая скорость и момент инерции блока; Атр – работа, совершаемая против сил трения в блоке, Ас – работа, совершаемая против сил сопротивления воздуха. Грузы и блок движутся равноускоренно, поэтому конечная скорость груза
, (15) где v – конечная скорость груза (его скорость на нулевой отметке); ω; и I – соответственно, конечная угловая скорость и момент инерции блока; Атр – работа, совершаемая против сил трения в блоке, Ас – работа, совершаемая против сил сопротивления воздуха. Грузы и блок движутся равноускоренно, поэтому конечная скорость груза , (16) где t – измеренное время движения системы, а конечная угловая скорость вращения блока:
, (16) где t – измеренное время движения системы, а конечная угловая скорость вращения блока: , (17) где r – радиус блока; r = 0,042 м.
, (17) где r – радиус блока; r = 0,042 м. , (18) масса блока – М = (8,50 ± 0,05) г.
, (18) масса блока – М = (8,50 ± 0,05) г.
 (19)
(19) . (20)
. (20) . (21)
. (21) = 9,81 м/с2, можно убедиться, что численные значения левой и правой частей равенства (21) совпадают с точностью до ошибок измерения. Тем самым экспериментально подтверждается закон сохранения и превращения механической энергии, так как равенство (21) является прямым следствием этого закона.
= 9,81 м/с2, можно убедиться, что численные значения левой и правой частей равенства (21) совпадают с точностью до ошибок измерения. Тем самым экспериментально подтверждается закон сохранения и превращения механической энергии, так как равенство (21) является прямым следствием этого закона.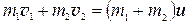 . (22) Отсюда общая скорость шаров после удара:
. (22) Отсюда общая скорость шаров после удара: .(23)
.(23) равна разности между их кинетической энергией до удара
равна разности между их кинетической энергией до удара 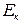 и ее потерями на совершение работы деформации А:
и ее потерями на совершение работы деформации А:  .
. ,
, .
. , (24) т.е. она пропорциональна квадрату относительной скорости соударяющихся тел
, (24) т.е. она пропорциональна квадрату относительной скорости соударяющихся тел  и зависит от соотношения их масс.
и зависит от соотношения их масс. ;(25)
;(25)
 ; (27)
; (27) . (28)
. (28) (29)
(29) , тогда
, тогда  . Из ΔАОВ имеем:
. Из ΔАОВ имеем:  , откуда
, откуда  , тогда
, тогда , (30) где l – длина нити. Аналогично можно определить скорости шаров после удара по их амплитудному отклонению (α1 – для шара 1, α2 – для шара 2):
, (30) где l – длина нити. Аналогично можно определить скорости шаров после удара по их амплитудному отклонению (α1 – для шара 1, α2 – для шара 2): ;
;  . (31)
. (31) , (32) причем α2 нужно брать со знаком минус, если после удара шар 2 отклонится в сторону, противоположную к направлению его движения до удара. Массы используемых шаров: m 1 = (105,00 ± 0,05) г, m 2 = (112,50 ± 0,05) г, длина подвеса шаров l = (49,00 ± 010) см. Шар 2 в отклоненном состоянии удерживается электромагнитом при отжатой кнопке «Пуск» на электронном блоке, при нажатии этой кнопки шар освобождается. Устанавливая один и тот же угол начального отклонения шара 2 (например, α = 10°), проведите серию измерений значения угла отклонения α1 шара 1 после удара, затем для шара 2 (α2). При выполнении работы в паре эти измерения можно совместить.
, (32) причем α2 нужно брать со знаком минус, если после удара шар 2 отклонится в сторону, противоположную к направлению его движения до удара. Массы используемых шаров: m 1 = (105,00 ± 0,05) г, m 2 = (112,50 ± 0,05) г, длина подвеса шаров l = (49,00 ± 010) см. Шар 2 в отклоненном состоянии удерживается электромагнитом при отжатой кнопке «Пуск» на электронном блоке, при нажатии этой кнопки шар освобождается. Устанавливая один и тот же угол начального отклонения шара 2 (например, α = 10°), проведите серию измерений значения угла отклонения α1 шара 1 после удара, затем для шара 2 (α2). При выполнении работы в паре эти измерения можно совместить.


