Практическая часть. 1. В четырёхугольнике АВСD (рис.2) АВ = ВС, АD = DC
1. В четырёхугольнике АВСD (рис.2) АВ = ВС, АD = DC. Докажите, что углы А и С равны.
Параллелограмм 2Найдите углы параллелограмма АВСD (рис.3). 3. Найдите углы параллелограмма, если: а) один из углов на 56° больше другого; б) в 3 раза меньше другого. 4. Периметр параллелограмма равен 126 см. Найдите его стороны, если две из них относятся как 4:5. 5. В параллелограмме АВСD АВ = 7 см, АD = 12 см. Биссектриса угла А пересекает сторону ВС в точке Е. Найдите отрезки ВЕ и ЕС. 6. В четырёхугольнике АВСD (рис.4) АD = ВС, <1 = <2. Докажите, что АВСD – параллелограмм. Прямоугольник. 7. Докажите, что в прямоугольном треугольнике медиана, проведённая из вершины прямого угла равна половине гипотенузы. 8. В прямоугольнике АВСD 9. Перпендикуляры, опущенные из точки пересечения диагоналей прямоугольника на две его соседние стороны, равны 5см и 7см. Найдите периметр прямоугольника. Ромб. 10. Докажите, что если две соседние стороны параллелограмма равны, то он является ромбом. 11. АВСD - ромб 6. В ромбе АВСD известно, что <С = 140°, а диагонали пересекаются в точке О. Найдите углы ΔАОВ. 12. Отрезки ВF и DE – высоты ромба АВСD 13. Угол между высотой и диагональю ромба, проведёнными из одной вершины, равен 42°. Найдите углы ромба.
|
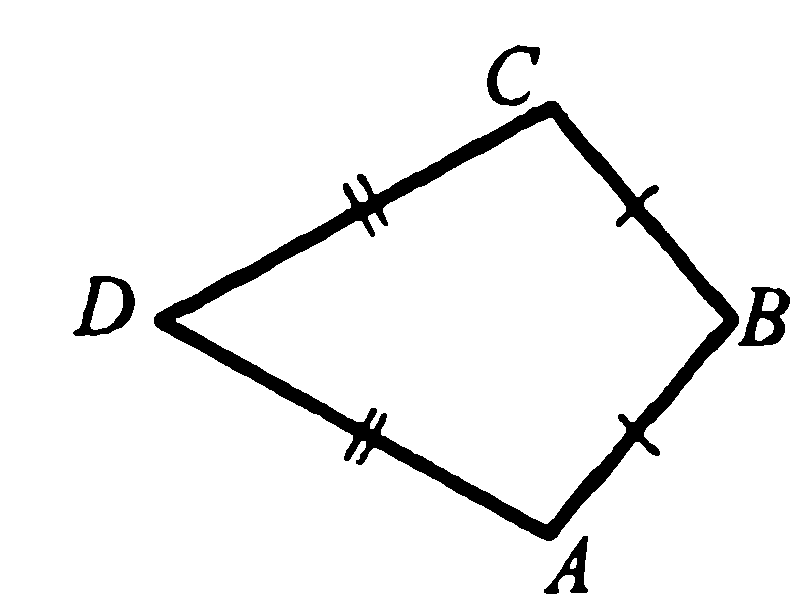рис.2 
рис.3 
рис.4 
рис.5.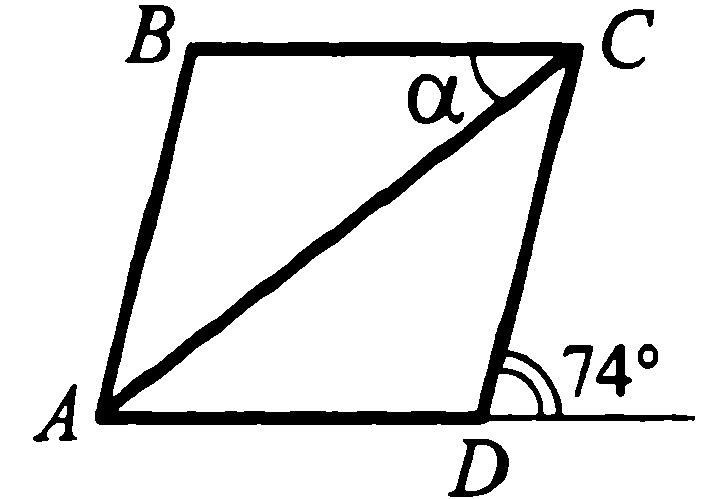
Найдите угол α.
Докажите, что BF = DE.
