Теоретическая часть. 12. Концепция общенациональной системы выявления и развития молодых талантов (утв

12. Концепция общенациональной системы выявления и развития молодых талантов (утв. Президентом РФ 03.04.2012 г.)

13. Постановление Главного государственного санитарного врача РФ от 15.05. 2013 г. № 26 «Об утверждении СанПиН 2.4.1.3049-13 "Санитарно-эпидемиологические требования к устройству, содержанию и организации режима работы дошкольных образовательных организаций"».

Письма, планы мероприятий

14. Письмо Минобразования России от 17.05.1995 г. № 61/19-12 «О психолого-педагогических требованиях к играм и игрушкам в современных условиях» (вместе с Порядком проведения психолого-педагогической экспертизы детских игр и игрушек, Методическими указаниями к психолого-педагогической экспертизе игр и игрушек, Методическими указаниями для работников дошкольных образовательных учреждений «О психолого-педагогической ценности игр и игрушек»).

15. Письмо Минобрнауки России от 17.11. 2011 г. № 03-877 «О реализации приказа Минобрнауки России от 20.07.2011 г. № 2151 "Примерный перечень игрового оборудования для учебно-методического обеспечения дошкольных образовательных учреждений и групп для детей дошкольного возраста, организованных в образовательных учреждениях"».

16. План мероприятий по формированию независимой системы оценки качества работы организаций, оказывающих социальные услуги, на 2013 - 2015 годы (утвержден распоряжением Правительства РФ от 30.03.2013 г. № 487-р).

17. Письмо Минобрнауки России от 07.06.2013 г. № ИР-535/07 «О коррекционном и инклюзивном образовании детей».

18. Письмо Департамента государственной политики в сфере общего образования Минобрнауки России от 08.08.2013 г. № 08-1063 «О рекомендациях по порядку комплектования дошкольных образовательных учреждений».

19. Письмо Минобрнауки России от 01.10.2013 № 08-1408 «О направлении методических рекомендаций по реализации полномочий органов государственной власти субъектов Российской Федерации» (вместе с «Методическими рекомендациями по реализации полномочий органов государственной власти субъектов Российской Федерации по финансовому обеспечению оказания государственных и муниципальных услуг в сфере дошкольного образования»).

20. Письмо Минобрнауки России от 14.10.2013 г. «Методические рекомендации по проведению независимой системы оценки качества работы образовательных организаций».

21. План действий по обеспечению введения ФГОС дошкольного образования (утвержден 31.12.2013 г. первым зам. Министра образования и науки РФ).

22. Письмо Рособрнадзора от 07.02.2014 г. № 01-52-22/05-382 «О недопустимости требования от организаций, осуществляющих образовательную деятельность по программам дошкольного образования, немедленного приведения уставных документов и образовательных программ в соответствие с ФГОС ДО».

Теоретическая часть.

Четырёхугольники

Трапеции

Параллелограммы Параллелограмм

Прямоугольники

Ромбы

Квадраты

 

Параллелограммом называется четырёхугольник, у которого каждые две противолежащие стороны параллельны.

Свойства параллелограмма.		Признаки параллелограмма
1. Противолежащие стороны параллелограмма равны. 2.Противолежащие углы параллелограмма равны. 3.Диагонали параллелограмма точкой пересечения делятся пополам.	1.Если в четырёхугольнике две противолежащие стороны равны и параллельны, то этот четырёхугольник параллелограмм. 2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм. 3.Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

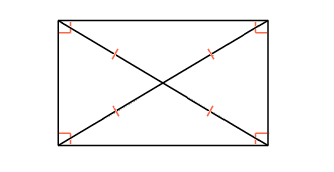
Прямоугольником называется параллелограмм, у которого все углы прямые.

Свойства прямоугольника.		Признаки прямоугольника.
1.Диагонали прямоугольника равны.	1.Если один из углов параллелограмма прямой, то этот параллелограмм – прямоугольник. 2.Если диагонали параллелограмма равны, то этот параллелограмм – прямоугольник.

Ромбом называется параллелограмм, у которого все стороны равны.

Свойства ромба.		Признаки ромба.
1.Диагонали ромба перпендикулярны, и являются биссектрисами его углов	1.Если диагонали параллелограмма перпендикулярны, то этот параллелограмм – ромб.

Квадратом называется прямоугольник, у которого все стороны равны; либо квадратом называется ромб, у которого все углы прямые.

Замечание: исходя из определения, квадрат имеет все свойства прямоугольника и ромба.

 

Теорема 2. Противолежащие стороны параллелограмма равны.

В С Дано:АВСD - параллелограмм.

А D Доказать:АВ = СD и ВС = АD.

Доказательство:1) Проведем диагональ АС;2) Δ АВС и Δ АСD равны по второму признаку равенства треугольников; 3) Т.о. АВ = СD.