Краткие теоретические сведения. 1 Александров А.В. и др. Сопротивление материалов М., "Высшая школа", 1995 г., стр
Лабораторная работа № 4 по дисциплине «Механика разрушения»
для специальности 1-54 01 02 – «Методы и приборы контроля качества и диагностики состояния объектов»
Расчеты на прочность при кручении. Определение модуля сдвига при испытании на кручение стального образца
Составитель: канд. техн. наук, доцент И.М. кузменко
Могилев, 2011г.
Цель работы. Изучить методы расчета бруса круглого поперечного сечения на прочность и жесткость. Определить величину модуля упругости второго рода и проверить справедливость закона Гука при кручении.
Краткие теоретические сведения. Кручение – вид нагружения, при котором на стержень действуют пары сил, расположенные в плоскости, перпендикулярной к его оси. Эти силы вызывают внешние (скручивающие) моменты. Стержни круглого или кольцевого сечения, работающие на кручение, называют валами. В поперечных сечениях скручиваемого вала под действием внешних моментов m возникает внутренний силовой фактор – крутящий момент ( В поперечных сечениях вала диаметром d и длиной ℓ действуют только непрерывно распределенные касательные напряжения
Касательные напряжения определяются по формуле:
где Мк – крутящий момент. Из условия равновесия Мк = m. ρ –текущий радиус точек сечения. Ip – полярный момент инерции.
Из формулы (4. 1) следует при
Геометрические характеристики вала, используемые в расчетах на прочность и жесткость при кручении: полярный момент инерции сечения полярный момент сопротивления сечения Как уже было отмечено, при кручении в поперечных сечениях действуют только касательные напряжения. Но нужно принять во внимание, что касательные напряжения будут действовать и в продольных сечениях вала. Это утверждение принимается на основании закона парности касательных напряжений. При этом сохраняется длина стержня и его диаметр (только для круглого поперечного сечения). Т.е. каждое поперечное сечение поворачивается в своей плоскости как жесткое целое. Следовательно, к скручиваемому вала применима гипотеза плоских и жестких сечений. Таким образом, можно сказать, что напряженное состояние в точках скручиваемого вала представляет собой чистый сдвиг. Закон Гука для чистого сдвига:
где
Деформацию вала оценивают (рисунок 4.3) абсолютным углом закручивания, величина которого определяется по формуле:
где Мк – крутящий момент на участке вала, Н·м; ℓ; – длина участка, на котором действует крутящий момент, м; G – модуль сдвига (модуль упругости второго рода), Па; Ip – полярный момент инерции поперечного сечения рассматриваемого участка вала, м4.
Рисунок 4.3 – К определению абсолютного угла закручивания
|

 ). Крутящий момент является равнодействующей внутренних сил.
). Крутящий момент является равнодействующей внутренних сил.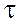 (рисунок 4.1).
(рисунок 4.1).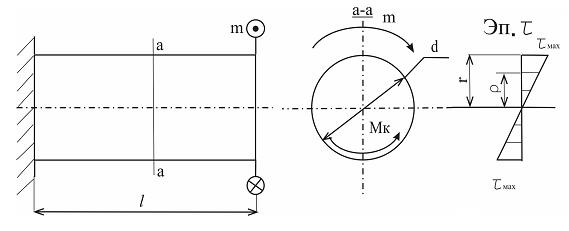 Рисунок 4.1 – Эпюра распределения касательных напряжений.
Рисунок 4.1 – Эпюра распределения касательных напряжений.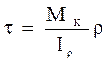 (4. 1)
(4. 1)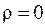 :
: 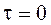 ; при
; при 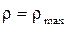 = r:
= r: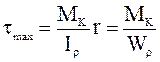 (4.2)
(4.2)
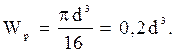
 (4.3)
(4.3)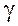 – угол сдвига произвольного прямоугольного элемента АВСD, лежащего на поверхности бруса (рисунок 4.2), образованного линиями сетки, нанесенной на поверхность вала.
– угол сдвига произвольного прямоугольного элемента АВСD, лежащего на поверхности бруса (рисунок 4.2), образованного линиями сетки, нанесенной на поверхность вала. Рисунок 4.2 – Деформация бруса
Рисунок 4.2 – Деформация бруса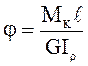 (4.4)
(4.4)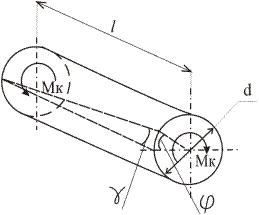 Формула (4.4) выражает закон Гука при кручении, согласно которому существует прямая зависимость между внутренним силовым фактором (
Формула (4.4) выражает закон Гука при кручении, согласно которому существует прямая зависимость между внутренним силовым фактором ( ) и абсолютным углом закручивания (
) и абсолютным углом закручивания (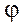 ). Величина GIp является жесткостью вала при кручении. Чем больше величина жесткости, тем меньше деформация стержня.
). Величина GIp является жесткостью вала при кручении. Чем больше величина жесткости, тем меньше деформация стержня.


