Аудиторное задание
1. А.П. Рябушко, В.В. Бархатов, В.В. Державец, И.Е. Юруть, Индивидуальные задания по высшей математике, - Мн.: Выш. Шк., 2000, 303 с. 2. А.П. Рябушко, В.В. Бархатов, В.В. Державец, И.Е. Юруть, Индивидуальные задания по высшей математике, Часть 2- Мн.: Выш. Шк., 2002, 396 с. 3. А.П. Рябушко, В.В. Бархатов, В.В. Державец, И.Е. Юруть, Индивидуальные задания по высшей математике, Часть 3- Мн.: Выш. Шк., 2002, 288 с. 4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, Ч.1: Учеб. Пособие для втузов. – М.: Высш. Школа, 1999, - 304 с. 5. Сборник задач по математике для втузов. Линейная алгебра и основы математического анализа, под редакцией А.В. Ефимова, Б.П. Демидовича.– М.: Наука, 1981, 464 с.
Практическое занятие 12-2часа Предмет теории вероятностей. Классическая и статистическая вероятности. Геометрическая вероятность Вопросы 1. Предмет теории вероятности. 2. Виды событий. 3. Классическое определение вероятности. 4. Частота событий. 5. Статистическое определение вероятности. 6. Геометрическое определение вероятности. Пример 1. По мишени производят три выстрела: Пусть а) б) в) Пример 2. Брошены две игральные кости. Пусть событие а) Ошибочное решение. Всего возможно 2 случая: Это ошибка, так как б) Всего равновозможных случаев Пример 3. Монета подбрасывается три раза, найти вероятность того, что при этом (безразлично, в каком порядке) выпадет два раза герб и один раз цифра. Решение. 1. Опыт (испытание, эксперимент) состоит в трехкратном подбрасывании монеты (или однократном подбрасывании трех монет). 2. Элементарным событием является любое сочетание последовательности выпадений сторон на трех подбрасываемых монетах. 3. U = {ггг, ццц, гцг, ццг, ггц, цгц, цгг, гцц}, N = 8. 4. Событие А – «выпадение двух гербов и одной цифры», M = 3. 5. P (A) = M / N = 3/8 = 0,375. Число размещений вычисляется по формуле: Число перестановок вычисляется по формуле: Число сочетаний находится по формуле Пример 4. Сколько всего семизначных телефонных номеров, в каждом из которых ни одна цифра не повторяется. Решение. Эта задача о размещении по 7 различным местам семи из 10 различных цифр, поэтому число номеров будет: Пример 5. Сколькими различными способами можно разложить восемь различных писем по восьми различным конвертам, если в конверте по одному письму. Решение. Пример 6. В городки играют 12 человек. Сколькими способами они могут набрать команду из 4 человек на соревнования? Решение. Число способов равно Пример7. Имеются изделия 4-х сортов, причем изделий i-ого сорта равно Решение. Вероятность вычисляется по классической формуле
Пример8. Среди n лотерейных билетов k выигрышных. Наудачу взяли m билетов. Определить вероятность того, что l выигрышных. Решение. Вероятность вычисляется по классической формуле
Пример9. Моменты начала двух случайных событийраспределены в промежутке времени между Решение. Сделаем рисунок.
Рисунок 1 Одно событие будем откладывать по оси ОХ, другое по оси ОУ. Пусть Т= у-5 £ х £ у+5. На чертеже это будет плоскость между прямыми АВ и СД, т.е. шестиугольник ОАВМДС. Второе неравенство равносильно двум: х ³10+у и х £ у-10. На чертеже это будут два треугольника KSP и ZFN. Для случая двумерного пространства формула геометрической вероятности будет:
где
для случая перекрывающихся по времени событий, а для случая не перекрывающихся во времени событий будет Аудиторное задание 1. В коробке 10 белых, 15 черных, 10 желтых и 25 красных шаров. Найти вероятность того, что наудачу взятый шар белый. 2. Сколько существует номеров автомобилей, состоящих из четырех разных цифр? 3. Бросаются две игральные кости. Определить вероятность того, что произведение числа очков делится на три 4. Сколькими возможными способами можно распределить между шестью лицами две разные путевки в санаторий.
|

 - попадание (промах) при первом выстреле
- попадание (промах) при первом выстреле 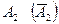 - при втором выстреле,
- при втором выстреле, 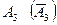 - при третьем выстреле. Тогда
- при третьем выстреле. Тогда - совместная группа равновозможных событий.
- совместная группа равновозможных событий. - полная группа несовместных событий,
- полная группа несовместных событий,  - событие, противоположное
- событие, противоположное  .
. - полная группа событий.
- полная группа событий. - сумма выпавших очков равна
- сумма выпавших очков равна  . Найти
. Найти 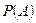 .
. - полная группа несовместных событий. Благоприятен одни случай, т.е.
- полная группа несовместных событий. Благоприятен одни случай, т.е. 
 . Благоприятные случаи: выпадение
. Благоприятные случаи: выпадение 
 =
=  .
. !.
!.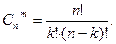


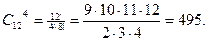
 (i=1,2,3,4). Для контроля наудачу берут m изделий. Определить вероятность того, что среди них
(i=1,2,3,4). Для контроля наудачу берут m изделий. Определить вероятность того, что среди них  первосортных,
первосортных, 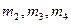 второго, третьего, четвертого сортов соответственно (
второго, третьего, четвертого сортов соответственно (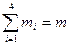 ).
). , где M- число благоприятные исходы (способов), N – общее число исходов (способов). Тогда они вычисляются по формулам:
, где M- число благоприятные исходы (способов), N – общее число исходов (способов). Тогда они вычисляются по формулам: .
.
 . Одно из событий длится
. Одно из событий длится  минут, другое
минут, другое 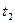 минут. Определить вероятность того, что: а) события перекрываются во времени; б) не перекрываются.
минут. Определить вероятность того, что: а) события перекрываются во времени; б) не перекрываются.
 . На рисунке 1 это отрезки OS и OF. По условию задачи: 0£ х £ Т, 0£ у £Т. Если события перекрываются во времени, то çх-уç£ min(
. На рисунке 1 это отрезки OS и OF. По условию задачи: 0£ х £ Т, 0£ у £Т. Если события перекрываются во времени, то çх-уç£ min( , а если не перекрываются во времени, то çх-уç³ mах(
, а если не перекрываются во времени, то çх-уç³ mах( . Первое неравенство равносильно следующему
. Первое неравенство равносильно следующему ,
, - площадь шестиугольника ОАВМДС, что соответствует благоприятствующему событию, S – площадь квадрата ОSMF. Окончательно, получим
- площадь шестиугольника ОАВМДС, что соответствует благоприятствующему событию, S – площадь квадрата ОSMF. Окончательно, получим




