Разложение функций в ряд Тейлора и его применение
1. А.П. Рябушко, В.В. Бархатов, В.В. Державец, И.Е. Юруть, Индивидуальные задания по высшей математике, - Мн.: Выш. Шк., 2000, 303 с. 2. А.П. Рябушко, В.В. Бархатов, В.В. Державец, И.Е. Юруть, Индивидуальные задания по высшей математике, Часть 2- Мн.: Выш. Шк., 2002, 396 с. 3. А.П. Рябушко, В.В. Бархатов, В.В. Державец, И.Е. Юруть, Индивидуальные задания по высшей математике, Часть 3- Мн.: Выш. Шк., 2002, 288 с. 4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, Ч.1: Учеб. Пособие для втузов. – М.: Высш. Школа, 1999, - 304 с. 5. Сборник задач по математике для втузов. Линейная алгебра и основы математического анализа, под редакцией А.В. Ефимова, Б.П. Демидовича.– М.: Наука, 1981, 464 с.
Практическое занятие 11-2часа Ряды Тейлора. Разложения элементарных функций в ряд Тейлора. Применения ряда Тейлора Разложение функций в ряд Тейлора и его применение Пример 1. 1) Разложить по степеням разности x-1 функцию y= x4-2x3+2x+2 Формула Тейлора: f(x)=f(a)+ Для того чтобы воспользоваться формулой Тейлора при x0=1 найдем: y(1)=2, y¢(1)=(4x3-6x2+2)çx=1=0, y¢¢(1)=(12x2-12x)çx=1=0, y¢¢¢(1)=(24x+12)çx=1=12, yIV (1)=24, yV (x)=0, и т.д.
Следовательно, x4-2x3+2x+2=2+
Пример 2. Вычислить Разложение функции (-¥<x<¥) Подставим в формулу (1) значение
Так как остаток, знакочередующегося ряда |rn|£ Un+1 (и следствие из признака Лейбница остаток ряда |Rn |<Un+1), то достаточно найти член Un+1, для которого Un+1<d Тогда Sn даст значение функции требуемой точности. Очевидно, что уже третий член ряда Sin Пример 3. Вычислить
Почленно интегрируя, найдем:
Пример 4. Найти пять первых членов разложения в степенной ряд решения дифферен-циального уравнения y`=x2+y2, если y(1)=1. Из данного уравнения находим, что у`(1)=1+1=2. Дифференцируем исходное уравнение: y`` =2x+2yy`, y``(1)=6 y```=2+2 (y`)2 + 2y y``, y```(1)=22 yIV=4y`y``+2y`y``+2yy```, yIV(1)=116 и т.д. Подставляя найденные значения производных в ряд
Пример 5. Вычислить
при
поскольку уже третий член отбросить в силу того, что он меньше (из следствия признака Лейбница; Следовательно, Аудиторное задание 1. Разложить по степеням x+1 многочлен 2. Разложить в ряд по степеням x функцию 3. Найти разложение в степенной ряд по степеням х решения дифференциального уравнения (записать три первых, отличных от нуля, члена этого разложения). a) 4. Используя разложение подинтегральной функции в степенной ряд, вычислить указанный определенный интеграл с точностью до 0,001 а) 6. Вычислить указанную величину приближенно с заданной степенью точности а)
|



 (x-a)+
(x-a)+  (x-a)2+
(x-a)2+  (x-a)3+
(x-a)3+  (x-a)n+×××
(x-a)n+××× 

 с точностью d=10-3
с точностью d=10-3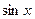 в степенной ряд
в степенной ряд  (1)
(1) . Тогда
. Тогда
 всегда удовлетворяет условию
всегда удовлетворяет условию поэтому с точностью
поэтому с точностью  -3
-3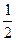



 dx с точностью до 0,01. Вычислим интеграл
dx с точностью до 0,01. Вычислим интеграл
 =1+
=1+  при любом t, то, подставляя (-x2) в место t, получим:
при любом t, то, подставляя (-x2) в место t, получим: 
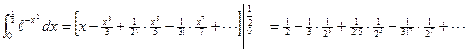
 Отсюда следует, что, ограничиваясь только двумя слагаемыми, мы получаем приближенное значение интеграла с точностью до 0,01:
Отсюда следует, что, ограничиваясь только двумя слагаемыми, мы получаем приближенное значение интеграла с точностью до 0,01: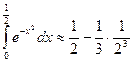 или
или 
 , получаем
, получаем
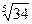 с точностью
с точностью 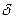 =10-3. Очевидно, что
=10-3. Очевидно, что 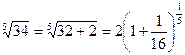 . Воспользуемся биноминальным рядом:
. Воспользуемся биноминальным рядом:


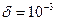
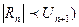


 и найти область сходимости полученного ряда.
и найти область сходимости полученного ряда. ; б)
; б)  ; в)
; в) 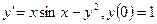 .
.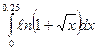 ; б)
; б)  ; в)
; в) 
 ; б)
; б)  ; в) arcsin
; в) arcsin