Вывод уравнения динамики объекта регулирования
1. Судовой паровой котёл с естественной циркуляцией представляется как единая ёмкость, в которой аккумулируется тепло. 2. Пренебрегаем инерционными свойствами пароперегревателя. 3. Рассматривается только пароводяной тракт котла, при этом не затрагивается газовоздушный тракт. 4. Пренебрегаем физическим теплом топлива, питательной воды и воздуха подаваемого в топку котла. 5. Коэффициент избытка воздуха α принимаем оптимальным и постоянным при любых нагрузках котла. Экспериментальные исследования динамических свойств судовых котлов показывают, что при возмущениях как внешних (расход пара), так и внутренних (расход топлива) разгонные характеристики по давлению пара несущественно отличаются от разгонных характеристик одноемкостных объектов со слабо выраженным самовыравниванием. Таким образом имеем упрощенное уравнение динамики котла как объекта регулирования давления пара – уравнение одноемкостного устойчивого объекта,
Количество тепла, аккумулированного в котле, может быть определено как,
где
Коэффициенты
Количество тепла, отведенного из котла,
где
Тогда время разгона,
Коэффициент самовыравнивания может быть определен как безразмерная разность частных производных по отводу и подводу тепла к парообразующей части котла:
где
Если уравнение (1) разделить на коэффициент самовыравнивания z, то получится представляющее собой классическую форму записи дифференциального уравнения:
где
|

 (1.1)
(1.1) - время разгона котла по давлению пара – время, в течение которого относительное изменение давления пара достигает величины, равной относительному ступенчатому изменению
- время разгона котла по давлению пара – время, в течение которого относительное изменение давления пара достигает величины, равной относительному ступенчатому изменению  или
или  , с;
, с; - относительное изменение давления пара;
- относительное изменение давления пара; - относительное изменение подвода тепла к парообразующей части котла;
- относительное изменение подвода тепла к парообразующей части котла;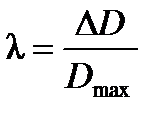 - относительное изменение паровой нагрузки;
- относительное изменение паровой нагрузки;
 – коэффициент аккумуляции тепла парообразующей части котла, показывающий, сколько нужно подвести (или отвести) тепла к парообразующей части котла, чтобы давление пара изменилось на 1кг/см²;
– коэффициент аккумуляции тепла парообразующей части котла, показывающий, сколько нужно подвести (или отвести) тепла к парообразующей части котла, чтобы давление пара изменилось на 1кг/см²;  – давление пара при номинальной нагрузке, кг/см². Значение
– давление пара при номинальной нагрузке, кг/см². Значение  может быть определено по формуле,
может быть определено по формуле,
 – коэффициенты, характеризующие соответственно долю воды, пара и метала в общей тепловой аккумуляции котла;
– коэффициенты, характеризующие соответственно долю воды, пара и метала в общей тепловой аккумуляции котла; – объемы воды и пара в котле, м³;
– объемы воды и пара в котле, м³; - масса металла котла, кг.
- масса металла котла, кг. определяются из таблиц водяного пара как,
определяются из таблиц водяного пара как,



 – расход пара – паспортная паропроизводительность котла, кг/с;
– расход пара – паспортная паропроизводительность котла, кг/с;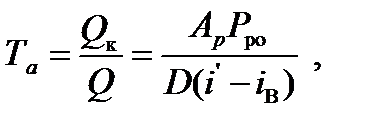 (1.5)
(1.5) - энтальпия воды, ккал/кг;
- энтальпия воды, ккал/кг; (1.6)
(1.6) – количество тепла, отведенное с паром;
– количество тепла, отведенное с паром; – количество тепла, подведенное с топливом;
– количество тепла, подведенное с топливом; , (1.7)
, (1.7) - постоянная времени объекта регулирования, с;
- постоянная времени объекта регулирования, с;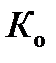 - коэффициент усиления объекта.
- коэффициент усиления объекта.


