Общие сведения. В лабораторной работе, выполняемой на ПЭВМ, изучаются ошибки измерения временного положения импульсного радиосигнала s(t)
Цель работы
Изучение механизмов образования ошибок измерения временного положения радиоимпульсного сигнала и способов обеспечения требуемой точности измерения
В лабораторной работе, выполняемой на ПЭВМ, изучаются ошибки измерения временного положения импульсного радиосигнала s(t), поступающего на вход измерительного приемника в смеси с белым шумом un(t):
Входное воздействие y(t) наблюдается на интервале времени T, обычно значительно большем, чем длительность сигнала t0. Оптимальный приемник (рисунок), вырабатывающий оценку максимального правдоподобия, состоит из фильтра СФ, согласованного с сигналом, амплитудного детектора АД и устройства, определяющего координату абсолютного максимума напряжения на выходе на интервале Т [1].
Моделирование фильтрации и детектирования, как правило, выполняют на основе метода комплексной огибающей [2], поскольку имитация сигналов на несущей (промежуточной) частоте f0 потребовала бы порядка 2f0T отсчетов сигнала равна П, то метод огибающей позволяет уменьшить число отсчетов до 2ПТ. Выигрыш в объеме вычислений определяется отношением f0/П и достигает десятков или даже сотен раз. В работе имитируется сигнал без внутриимпульсной модуляции с «колокольной» (гауссовской) огибающей
Сигнал воспроизводится в пределах
Если по этому же уровню определить и ширину амплитудного спектра
Значение огибающей «на границах» сигнала
составляет всего 1% от максимального значения S0. При таком достаточно полном воспроизведении сигнала его параметры (эффективные длительность и ширина спектра, энергия и др.) могут вычисляться без учета ограничения физической длительности. Например, энергия может быть определена по формуле
расширение пределов интегрирования в которой до бесконечных существенно упрощает результат. Аналогично можно определить нормированную автокорреляционную функцию сигнала
Откуда легко находится эффективная ширина спектра
При имитации белого шума, имеющего, как известно, бесконечную дисперсию, дискретный эквивалент представляется [3] последовательностью гауссовских некоррелированных чисел с дисперсией Обработка смеси сигнала с шумом приводит к образованию на выходе АД напряжения, подчиняющегося обобщенному распределению Релея. Огибающая нормированной корреляционной функции шума на выходе СФ совпадает с корреляционной функцией сигнала
Если, по аналогии с определением полной длительности сигнала В работе изучаются ошибки измерения временного положения сигнала (ИВПС) трех видов: – нормальные ошибки, вызванные действием шума; -аномальные ошибки; -ошибки, обусловленные дискретизацией сигнала. Соответствующей манипуляцией параметров модели значения отдельных составляющих ошибки могут быть сделаны незначительными, что позволяет изучать влияние оставшихся компонентов. Из трех перечисленных типов ошибок здесь остановимся подробно на аномальных в силу их особенной специфики, а также определенной сложности регистрации в эксперименте. Как известно [1], они возникают при слабом сигнале, когда выбросы шума на выходе АД (см.рисунок) могут превысить значение смеси сигнала с шумом. В этих случаях результат измерения
Выражение (1) определяет условную дисперсию ошибок- при условии, что аномальное измерение состоялось. Безусловная дисперсия ошибок с учетом альтернативного результата определяется формулой
В которой
- дисперсия нормальных измерений (потенциальная точность);
Для ее нахождения разобьем интервал Т на М=ЕПэ/2,5 подынтервалов длиной Введем локальную вероятность аномального измерения
Полную вероятность аномального измерения в силу некоррелированности отчетов шума, отстоящих на интервал 2,5/Пэ , приближенного определим выражением
Представляя (1) и (3) в (2) и переходя к относительной ошибке
Величина Обычно интересуется зависимостью При экспериментальном определении вероятности аномального измерения
Что обусловлено следующими соображениями. Полная длительность полезного сигнала (“по нулям”) на входе СФ и АД (см. рисунок) составляет Известно. Что дисперсия статистического измерения вероятности
Откуда необходимый объем статистического эксперимента
Где
|

 ,
, 


 , следовательно параметр
, следовательно параметр  имеет смысл его полной длительности. Параметр
имеет смысл его полной длительности. Параметр  , входящий во второе из этих выражений, является наиболее распространенным определением длительности «колокольного» импульса, определяемой по уровню
, входящий во второе из этих выражений, является наиболее распространенным определением длительности «колокольного» импульса, определяемой по уровню
 этой огибающей, то оказывается
этой огибающей, то оказывается  . Этим и объясняется общепринятость такого определения
. Этим и объясняется общепринятость такого определения 
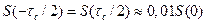
 ,
, ,
, .
. , где N0 – спектральная плотность мощности помехи un(t).
, где N0 – спектральная плотность мощности помехи un(t). , что является следствием согласованной фильтрации. С помощью приведенных выше выражений, можно записать
, что является следствием согласованной фильтрации. С помощью приведенных выше выражений, можно записать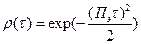 .
. , то интервал корреляции
, то интервал корреляции  . При прохождении шума через детектор происходит некоторое расширение его спектра и, следовательно, уменьшение интервала корреляции. Поэтому в качестве оценки интервала корреляции шума на выходе АД примем значение
. При прохождении шума через детектор происходит некоторое расширение его спектра и, следовательно, уменьшение интервала корреляции. Поэтому в качестве оценки интервала корреляции шума на выходе АД примем значение 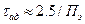 .
. t0 существенно отличается от t0, что и оправдывает название таких ошибок. Очевидно, что
t0 существенно отличается от t0, что и оправдывает название таких ошибок. Очевидно, что  – равномерно распределенная на интервале (0,Т) случайная величина с математическим ожиданием Т/2 и дисперсией Т2 /12.
– равномерно распределенная на интервале (0,Т) случайная величина с математическим ожиданием Т/2 и дисперсией Т2 /12. (1)
(1) (2)
(2) (3)
(3) - отношение сигнал/шум (ОСШ);
- отношение сигнал/шум (ОСШ); - вероятность возникновения аномального результата.
- вероятность возникновения аномального результата. , приближено определяющей длительность интервала корреляции выходного шума. Последнее дает возможность рассматривать отсчеты шума из различных подынтегралов как независимые, что существенно облегчает анализ аномальных измерений.
, приближено определяющей длительность интервала корреляции выходного шума. Последнее дает возможность рассматривать отсчеты шума из различных подынтегралов как независимые, что существенно облегчает анализ аномальных измерений.

 , получим
, получим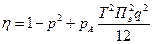
 характеризует меру увеличения ошибок (по отношению к нормальным), вызванного аномальными измерениями. Непосредственное измерение дисперсии
характеризует меру увеличения ошибок (по отношению к нормальным), вызванного аномальными измерениями. Непосредственное измерение дисперсии  (или нормированной дисперсии
(или нормированной дисперсии  . Располагая этой зависимостью, можно определить пороговое значение ОСШ, при превышении которого обеспечивается нормальный режим измерения. При уменьшении
. Располагая этой зависимостью, можно определить пороговое значение ОСШ, при превышении которого обеспечивается нормальный режим измерения. При уменьшении  (пропорционально, согласно
(пропорционально, согласно  ) величина этого вклад оказывается доминирующей в (2) уже при весьма малых значениях
) величина этого вклад оказывается доминирующей в (2) уже при весьма малых значениях 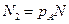 , в которых наблюдаются аномальные результаты, оказывается существенно меньше общего числа экспериментов N. Для получения статистических достоверных результатов измерения
, в которых наблюдаются аномальные результаты, оказывается существенно меньше общего числа экспериментов N. Для получения статистических достоверных результатов измерения  оказывается непосильным даже для ПЭВМ с высокой производительностью. Как показывает более тонкий количественный анализ, зависимости
оказывается непосильным даже для ПЭВМ с высокой производительностью. Как показывает более тонкий количественный анализ, зависимости  от
от  , (5)
, (5) , следовательно, его влияние на выходное напряжение АД проявляется в пределах этого временного интервала. Поэтому появление оценки
, следовательно, его влияние на выходное напряжение АД проявляется в пределах этого временного интервала. Поэтому появление оценки 

 - относительная дисперсия измерения вероятности
- относительная дисперсия измерения вероятности 


