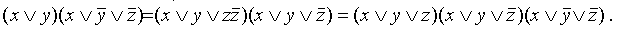ДНФ, СДНФ, КНФ, СКНФ
Менеджер дилерского отдела ООО "Позитрон-Пласт" Сот.тел.: 89116645589 E-mail: eka72751175@yandex.ru
Заявка на участие в концертах. Меня зовут____________________________ Телефон для связи +7____________________ Я хочу принимать участие в концертах «Живой Звук» в качестве: · Гостя · Исполнителя (отметить нужное) Друзья напоминаем вам, что исполнение песни на профессиональном оборудовании под аккомпанемент группы «Живой Звук» оплачивается в размере - 1000 руб/песня. В качестве исполнителя, я хочу: · Исполнить песни из репертуара · Заказать мои любимые песни в репертуар группы (отметить нужное) Обычно я люблю петь (перечислить несколько песен или исполнителей):
Репертуар группы можно посмотреть тут: Группа Вконтакте http://vk.com/jivoykaraoke Наш сайт http://mjsound.pro/ Для связи: Почта guitar.party@gmail.com
ДНФ, СДНФ, КНФ, СКНФ Простой конъюнкцией называется конъюнкция одной или нескольких переменных, при этом каждая переменная встречается не более одного раза (либо сама, либо ее отрицание). Например, Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций. Например, выражение Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одном и том жепорядке. Например, выражение Аналогичные определения (с заменой конъюнкции на дизъюнкцию и наоборот) верны для КНФ и СКНФ. Приведем точные формулировки. Простой дизъюнкцией называется дизъюнкция одной или нескольких переменных, при этом каждая переменная входит не более одного раза (либо сама, либо ее отрицание).Например, выражение Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций (например выражение Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке. Например, выражение Приведем алгоритмы переходов от одной формы к другой. Естественно, что в конкретных случаях (при определенном творческом подходе) применение алгоритмов бывает более трудоемким, чем простые преобразования, использующие конкретный вид данной формы: а) переход от ДНФ к КНФ Алгоритм этого перехода следующий: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения (или правила Блейка). Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:
Заметим, что КНФ можно получить и из первоначального выражения, если вынести у за скобки; б) переход от КНФ к ДНФ Этот переход осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения)
Таким образом, получили ДНФ. Обратный переход (от СДНФ к ДНФ) связан с проблемой минимизации ДНФ. Подробнее об этом будет рассказано в разд. 5, здесь же мы покажем, как упростить ДНФ (или СДНФ) по правилу Блейка. Такая ДНФ называется сокращенной ДНФ; в) сокращение ДНФ (или СДНФ) по правилу Блейка Применение этого правила состоит из двух частей: - если среди дизъюнктных слагаемых в ДНФ имеются слагаемые - если добавляемое слагаемое уже содержалось в ДНФ, то его можно отбросить совсем, например, или
Разумеется, сокращенная ДНФ не определяется единственным образом, но все они содержат одинаковое число букв (например, имеется ДНФ
в) переход от ДНФ к СДНФ Если в какой-то простой конъюнкции недостает переменной, например, z, вставляем в нее выражение
г) переход от КНФ к СКНФ Этот переход осуществляется способом, аналогичным предыдущему: если в простой дизъюнкции не хватает какой-то переменной (например, z, то добавляем в нее выражение
Таким образом, из КНФ получена СКНФ. Заметим, что минимальную или сокращенную КНФ обычно получают из соответствующей ДНФ.
|

 является простой конъюнкцией,
является простой конъюнкцией,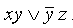 является ДНФ.
является ДНФ.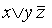 является ДНФ, но не СДНФ. Выражение
является ДНФ, но не СДНФ. Выражение 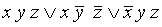 является СДНФ.
является СДНФ. – простая дизъюнкция,
– простая дизъюнкция, – КНФ).
– КНФ).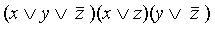 является СКНФ.
является СКНФ.
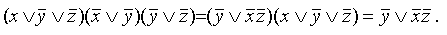
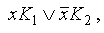 , то ко всей дизъюнкции добавляем слагаемое К 1 К 2. Проделываем эту операцию несколько раз (можно последовательно, можно одновременно) для всех возможных пар слагаемых, а затем, применяем обычное поглощение;
, то ко всей дизъюнкции добавляем слагаемое К 1 К 2. Проделываем эту операцию несколько раз (можно последовательно, можно одновременно) для всех возможных пар слагаемых, а затем, применяем обычное поглощение;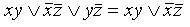

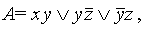 , после применения к ней правила Блейка можно прийти к ДНФ, равносильной данной):
, после применения к ней правила Блейка можно прийти к ДНФ, равносильной данной):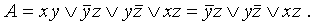
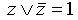 ,после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем). Например:
,после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем). Например: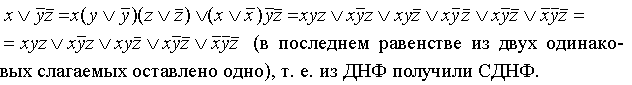
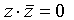 (это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона):
(это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона):