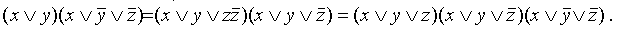Банк заданий в тестовой форме. Например, выражение является СКНФ.
Например, выражение Приведем алгоритмы переходов от одной формы к другой. Естественно, что в конкретных случаях (при определенном творческом подходе) применение алгоритмов бывает более трудоемким, чем простые преобразования, использующие конкретный вид данной формы: а) переход от ДНФ к КНФ Алгоритм этого перехода следующий: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения (или правила Блейка). Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:
Заметим, что КНФ можно получить и из первоначального выражения, если вынести у за скобки; б) переход от КНФ к ДНФ Этот переход осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения)
Таким образом, получили ДНФ. Обратный переход (от СДНФ к ДНФ) связан с проблемой минимизации ДНФ. Подробнее об этом будет рассказано в разд. 5, здесь же мы покажем, как упростить ДНФ (или СДНФ) по правилу Блейка. Такая ДНФ называется сокращенной ДНФ; в) сокращение ДНФ (или СДНФ) по правилу Блейка Применение этого правила состоит из двух частей: - если среди дизъюнктных слагаемых в ДНФ имеются слагаемые - если добавляемое слагаемое уже содержалось в ДНФ, то его можно отбросить совсем, например, или
Разумеется, сокращенная ДНФ не определяется единственным образом, но все они содержат одинаковое число букв (например, имеется ДНФ
в) переход от ДНФ к СДНФ Если в какой-то простой конъюнкции недостает переменной, например, z, вставляем в нее выражение
г) переход от КНФ к СКНФ Этот переход осуществляется способом, аналогичным предыдущему: если в простой дизъюнкции не хватает какой-то переменной (например, z, то добавляем в нее выражение
Таким образом, из КНФ получена СКНФ. Заметим, что минимальную или сокращенную КНФ обычно получают из соответствующей ДНФ.
Банк заданий в тестовой форме
|

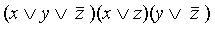 является СКНФ.
является СКНФ.
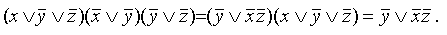
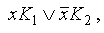 , то ко всей дизъюнкции добавляем слагаемое К 1 К 2. Проделываем эту операцию несколько раз (можно последовательно, можно одновременно) для всех возможных пар слагаемых, а затем, применяем обычное поглощение;
, то ко всей дизъюнкции добавляем слагаемое К 1 К 2. Проделываем эту операцию несколько раз (можно последовательно, можно одновременно) для всех возможных пар слагаемых, а затем, применяем обычное поглощение;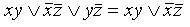

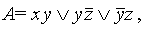 , после применения к ней правила Блейка можно прийти к ДНФ, равносильной данной):
, после применения к ней правила Блейка можно прийти к ДНФ, равносильной данной):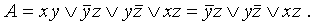
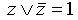 ,после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем). Например:
,после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем). Например: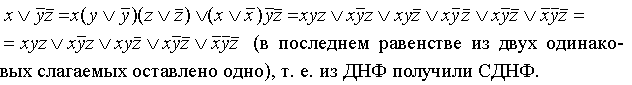
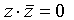 (это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона):
(это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона):