«ВЕКТОРНАЯ АЛГЕБРА»
 Занятие 1
Занятие 1
Примеры решения задач
Задача 1. В равнобедренной трапеции ОАСВ угол  ,
, 
 ,
,
 - середина сторон ВС и АС. Выразить векторы
- середина сторон ВС и АС. Выразить векторы  через
через  - единичные векторы направлений
- единичные векторы направлений 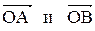 .
.
 В М С
В М С
 N
N
O A

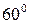
Решение.  . Так как
. Так как  . Найдем
. Найдем
вектор  . Из треугольника ОСА
. Из треугольника ОСА  , а так как
, а так как  , а
, а
 , вектор
, вектор  . Найдем
. Найдем  из треуголь-
из треуголь-
ника ONC  , а так как
, а так как  ,
,  ,
,  .
.
Из треугольника OMN  .
.
Задача 2. Даны векторы  и
и 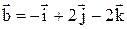 , приложены к общей точке. Найти орт биссектрисы угла между
, приложены к общей точке. Найти орт биссектрисы угла между 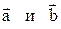 .
.
Решение. Диагональ четырехугольника совпадает с биссектрисой, если этот четырехугольник – ромб (квадрат). Найдя  , получим угол с одинаковыми по длине сторонами, равными единице. Таким образом, вектор
, получим угол с одинаковыми по длине сторонами, равными единице. Таким образом, вектор  направлен по биссектрисе угла между
направлен по биссектрисе угла между 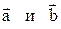 .
.
 ,
, 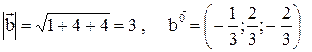 ,
,
 .
.
Найдем длину вектора 
 , тогда орт биссектрисы равен
, тогда орт биссектрисы равен 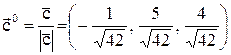 .
.
Задача 3. Разложить вектор  по трем некомпланарным векторам:
по трем некомпланарным векторам:  .
.
Решение.  .
.  .
.
Приравняем коэффициенты справа и слева:
 тогда
тогда 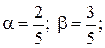
 и
и 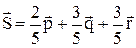 .
.
Задача 4. Даны точки 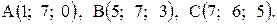
Разложить вектор  по ортам
по ортам  и найти его длину, направляющие косинусы, орт вектора
и найти его длину, направляющие косинусы, орт вектора  .
.
Если известны координаты точек  и
и  , то координаты вектора
, то координаты вектора 
Разложение этого вектора по ортам  :
: 
Длина вектора находится по формуле  а направляющие косинусы равны
а направляющие косинусы равны  Орт вектора
Орт вектора 
Найдем координаты векторов:


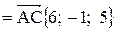 и
и 
Вектор 



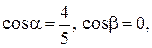

 Занятие 2
Занятие 2
Скалярное произведение векторов

 Занятие 1
Занятие 1 ,
, 
 ,
, - середина сторон ВС и АС. Выразить векторы
- середина сторон ВС и АС. Выразить векторы  через
через  - единичные векторы направлений
- единичные векторы направлений 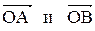 .
. В М С
В М С N
N
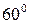
 . Так как
. Так как  . Найдем
. Найдем . Из треугольника ОСА
. Из треугольника ОСА  , а так как
, а так как  , а
, а , вектор
, вектор  . Найдем
. Найдем  из треуголь-
из треуголь- , а так как
, а так как  ,
,  ,
,  .
. .
. и
и 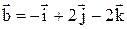 , приложены к общей точке. Найти орт биссектрисы угла между
, приложены к общей точке. Найти орт биссектрисы угла между 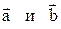 .
. , получим угол с одинаковыми по длине сторонами, равными единице. Таким образом, вектор
, получим угол с одинаковыми по длине сторонами, равными единице. Таким образом, вектор  направлен по биссектрисе угла между
направлен по биссектрисе угла между  ,
, 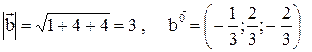 ,
, .
.
 , тогда орт биссектрисы равен
, тогда орт биссектрисы равен 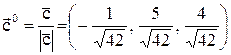 .
. по трем некомпланарным векторам:
по трем некомпланарным векторам:  .
. .
.  .
. тогда
тогда 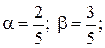
 и
и 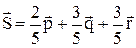 .
.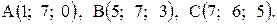
 по ортам
по ортам  и найти его длину, направляющие косинусы, орт вектора
и найти его длину, направляющие косинусы, орт вектора  .
. и
и  , то координаты вектора
, то координаты вектора 
 :
: 
 а направляющие косинусы равны
а направляющие косинусы равны  Орт вектора
Орт вектора 


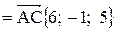 и
и 




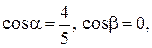

 Занятие 2
Занятие 2


