ПРАКТИЧЕСКИЕ
Прямаянаплоскости 1) Выписать нормальный вектор а) 5х-2у+7=0 б) 4х+9у=0 в) 5у+1=0 г) 3х+8=0 д) у=2 е) х=-3
2) Составить уравнения прямых, проходящих через данную точку М0 перпендикулярно данному вектору а) М0(2,-3) д) М0(1,4)
3) Составить уравнения прямых, проходящих через данную точку М0 параллельно данному вектору а) М0(1,-5)
4) Составить уравнения прямых, проходящих через две данные точки М1 и М2 а) М1(2,-7) М2(3,4); б) М1(1,-3) М2(5,-1); в) М1(1,8) М2(2,-7) г) М1(1,3) М2(1,-4); д) М1(3,-2) М2(5,-2); е) М1(2,7) М2(2,-1)
5) Составить уравнения прямых, отсекающих на осях координат отрезки а) а=2, в=-3 б) а=5, в=1 в) а=3, в=-4
6) Вычислить площадь треугольника, отсекаемого прямой l от координатного угла а) 3х-2у+6=0 б)-2х+у-4=0 в) х-5у-10=0
7) Рассмотреть пары прямых, выявить параллельные, перпендикулярные, найти угол между прямыми а) х-2у+7=0 (l1) б) 3х-6у+1=0 (l1) в) 2х-8у+5=0 (l1) г) х-8у+1=0 (l1) 2х-4у+1=0 (l2) 6х+3у-7=0 (l2) -х+4у+3=0 (l2) 8х+у-5=0 (l2) д) 3х-у+5=0 (l1) е) х-5у+1=0 (l1) 2х+у-7=0 (l2) 2х+3у-7=0 (l2)
8) При каком значении а) 2х-3у+5=0 l1 б) х -
9) При каком а)
10) Составить уравнение прямой l1, проходящей через данную точку М0 параллельно данной прямой l а) М0(5,-2) l: 3х-у=0 б) М0(1,0) l: х-2у+1=0 в) М0(1,-3) l: х-5у+2=0 г) М0(0,-3) l: х-6у=0
11) Составить уравнение прямой l1, проходящей через точку М0 перпендикулярно прямой l а) М0(2,-4) l: х+3у-2=0 б) М0(1,0) l: х-у+7=0 в) М0(1,-8) l: 3х+5=0 г) М0(2,0) l: 5у+2=0
12) Вычислить расстояние от точки М0 до прямой l а) М0(2,-7) l:х-2у+3=0 б) М0(2,-3) l:3у+7=0 в) М0(1,-2) l:2х+5=0
14) Даны вершины 16) Вычислить расстояние между параллельными прямыми а) l1: 3х-4у-10=0 б) l1:х-2у+1=0 в) l1:2х+у-7=0 l2: 6х-8у+5=0 l2:2х-4у+5=0 l2:4х+2у-1=0
17) Найти проекцию точки Р на прямую l а) Р(-6,4) l:4х-5у+3=0 б) Р(1,0) l:х+2у-5=0
18) Найти точки пересечения прямых а) х+5у-1=0 б) 3х-у+1=0 в) 2х+3у-5=0 2х-7у+4=0 х-2у+2=0 3х-5у+3=0
Плоскость 1)Составить уравнение плоскости, проходящей через точку М0 а) М0 (2,-1,3)
2)Выписать нормальные вектора плоскостей а) 3x-5y+2z-7=0 б) 5y-x+11=0 в) x-y+2z=0 г) 2y+z=0 д) x=-2 е) y=5 ж) z-3=0
1) Составить уравнение плоскости, проходящие через 3 данные точки М1, М2 и М3 а) М1 (1,2,-3) М2 (2,-1,0) М3 (1,5,2) б) М1 (5,-4,1) М2 (3,0,-2) М3 (1,2,1)
2) Составить уравнение плоскости, отсекающей на всех координат отрезки a,b,c. Построить плоскости а) a=5, b=2, c=-4 б) a=-2, b=2, c=1 в) a=3, b=-2, c=5
3) Построить плоскости и вычислить площади треугольников, которые эти плоскости отсекают от координатных углов. а) x+2y+3z-6=0 б) 2x-5y+z+10=0 в) 3x-5y+z-15=0
4) При каких значениях l и m плоскости параллельны? 926(1) 2x+ly+3z-5=0 mx-6y-6z+z=0
5) При каком l плоскости перпендикулярны? 927(1) 3x-5y+lz-3=0 x+3y+2z+5=0
8) Найти угол между плоскостями. 928 а) x-y в) 6x+3y-2z=0, x+2y+6z-12=0; г) x+2y+2z-3=0, 16x+12y-15z-1=0
10) Составить уравнения плоскостей, проходящих через а) точку М1(2,-3,5) параллельную плоскости oxy, б) точку М1(1,-5,1) параллельную плоскости oxz, в) точку М1(0,-1,2) параллельную плоскости oyz.
11) Составить уравнение плоскости а) М0 (5,1,-2) б) М0 (1,-2,1)
11)Вычислить расстояние от точки М0 до плоскости а) М0(2,3,-5) б) М0(1,0,1)
Прямая в пространстве
1. Составить канонические и параметрические уравнения прямых а) проходящей через точку М0(2,-1,3) параллельно вектору б) проходящей через точку М0(2,-3,1) параллельно вектору в) проходящей через две точки М1(5,-2,1) и М2(1,-3,4) г)
2. Выписать направляющий вектор прямой а) 3. Доказать параллельность прямых а) б) 4. Доказать перпендикулярность прямых а) б) 5. Найти угол между прямыми а) б)
в)
Прямая и плоскость в пространстве
1. Найти точку пересечения прямой и плоскости а) б) 2. При каком значении m прямая параллельна плоскости а) б) 3. При каких значениях А и В прямая перпендикулярна плоскости а) б) 4. Найти угол между прямой и плоскостью а) б) 5. Составить уравнение плоскости, проходящей через точку М(3,5,-4) перпендикулярно прямой 6. Составить уравнение перпендикуляра, опущенного из точки К(2,-1,3) на плоскость 3x-2y+z-5=0. 7.Найти проекцию точки А(2,-1,0) на плоскость x-2y+z-2=0
Вариант № 1
Вектор а длиной 2 ед. составляет с осями Ox и Oy углы α=600, β=1200. Вычислите компоненты вектора а.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 2
Вычислите площадь треугольника АВС, если А(1;2;0), В(3;0;3), С(5;2;6) и высоту, опущенную из вершины А на сторону ВС.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 3
Разложите вектор s = a + b + с по трем некомпланарным векторам m = a + b -2 c, n = a - b, p =2 b +3 c.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 4
Вершины пирамиды находятся в точках А (4;2;3), В(-5;-4;2), С(5;7;-4), D(6;4;-7), Найдите площадь сечения, проходящего через середину ребра AD и вершины пирамиды В и С.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 5
Векторы а = {4;-5;-4}, b = {5;-1;0} и с = {2;4;-3} заданы в ортонормирован- ном базисе. Найдите (а, b), | [ a, b ] |, (а, b, с).
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 6
Вершины пирамиды находятся в точках А(-9;-7;4), В(-4;3;-1), С(5;-4;2), D(3;4;4). Найдите площадь грани BCD и объем пирамиды ABCD.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 7
Сила F = {2,2,9} приложена к точке А (4,2,-3). Вычислите модуль момента силы F относительно точки В(2,4,0).
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 8
Даны три силы P ={7,3,-4}, Q ={3,-2,2} и R ={-5,4,3}, приложенные к точке А(-5,0,4). Вычислите работу, производимую равнодействующих этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку В(4,-3,5).
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 9
Даны векторы а = {-3,0,4}, b = {5,-2,-14}. Найдите единичный вектор е, который лежит на биссектрисе угла, образованного векторами а и b.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 10
Объем тетраэдра ABCD равен 5 ед3, три его вершины находятся в точках А(2,1,-1), В=(3,0,1), С(2,-1,3). Найдите четвертую вершину D, если она лежит на оси Оy.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 11
В трапеции ABCD AD =λ BC. Выразите векторы AС и BD через векторы AD и CD.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 12
Вектор х длиной 51 ед. перпендикулярен оси Oz и вектору а = {8,-15,3} и образует острый угол с осью Оx. Найдите координаты вектора х.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 13
Даны 2 точки А (1,2,3), и В (7,2,5). На прямой АВ найдите такую точку М, чтобы точки В и М были расположены по разные стороны от точки А и АМ=2АВ.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 14
К вершине куба приложены три силы, равные по величине 1, 2, и 3 и направленные по диагоналям граней куба, выходящих из данной вершины. Найдите величину равнодействующей этих трех сил и углы, образуемые ею с составляющими силами.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 15
Даны два вектора а = {8,4,1}, b = {2,-2,1}. Найдите вектор с, компланарный а и b, перпендикулярный вектору а,равный а по длине и образующий с b тупой угол.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 16
Напишите разложение вектора d = {2,-5,-13} по векторам а = {7,2,1}, b = {4,3,5} и с = {3;4;-2}.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 17
Найдите вектор х, зная, что он перпендикулярен векторам а = {3,2,2} и b = {18,-22,-5} и (х, с) = 2, где с = {0,0,2}.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 18
Даны точки А(1,-2,2), В(1,4,0), С(-4,1,1) и D(-5,-5,3). Докажите, что вектор АС перпендикулярен вектору ВD. Вычислите угол АВС.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 19
Является ли четырехугольник ABCD трапецией, если А(-1;1;2), В(2;-2;2), С(2;1;-3),D (-1;7;-8)?
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 20
Вычислите проекцию вектора а ={3;1;0} на ось вектора b ={2;-1;2} и проекцию вектора b на ось вектора а.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 21
Определите число z так, чтобы векторы a = {1;3;-1}, b = {2;-2;z}, c = ={3;1;5} были линейно зависимы.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 22
Пусть векторы а и b не коллинеарны и AB =
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 23
Даны векторы а = -3 i +2 j +7 k, b = i -5 k, с = 6 i +4 j - k. Вычислите (3 b, с), |[5 a,-2 c ]|. Коллинеарны или ортогональны векторы а и с?
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 24
Докажите, что векторы а = {6;-1}, b = {-3;5} образуют базис и найдите аналитически координаты векторы с = {9;3} в этом базисе. Сделайте чертеж.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 25
Найдите угол между единичными векторами е1 и е2, если известно, что векторы а = е1 +2 е2 и b = 5 е1 -4 е2 взаимно перпендикулярны.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 26
Дан правильный восьмиугольник А1 А2 …А8. Пусть А1А2 = а, А1А3 = b. Разложите векторы А5А8 и А3А6 по векторам а и b.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 27
Найдите большую диагональ параллелограмма, построенного на векторах а ={2,-1,3} и b ={-3,2,-1}.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 28
Отрезок AB разделен тремя точками C1, C2,C3 на 4 равные части. Найдите координаты точек C1, C2, C3, если А (3;-1;5), В (-2;5;-5).
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 29
Найдите смешанное произведение векторов (a +2 b,4 a - b, b -3 а).
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 30
Разложите вектор AB по векторам p ={1;1;-1}, q ={-2;2;2} и r ={3;-3;3}, где A(-3;1;5), B(2;-4;3)
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 31
Даны вершины треугольника ABC: A(3,2,1), B(-5,6,2), C(2,-3,4). Найдите длину медианы AD и косинус угла BAD.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 32
Найдите орт, перпендикулярный векторам a ={2;-1;3} и b ={4;3;-2}.
ФГБОУ ВПО “Тульский государственный университет” Кафедра математического моделирования
Дисциплина «Математика» Раздел «Векторная алгебра»
Вариант № 33
Два ребра куба лежат на векторах a =4 i +2 j -3 k, b = i +7 j +6 k. На каком векторе лежит третье ребро куба?
ПРАКТИЧЕСКИЕ
|

 и угловой коэффициент k прямых, построить прямые
и угловой коэффициент k прямых, построить прямые
 прямые параллельные?
прямые параллельные? . А(1,1) В(3,3) С(5,2) найти: 1) уравнение и длину стороны АС, 2) уравнение и длину медианы ВМ, 3) уравнение и длину высоты ВК, 4)
. А(1,1) В(3,3) С(5,2) найти: 1) уравнение и длину стороны АС, 2) уравнение и длину медианы ВМ, 3) уравнение и длину высоты ВК, 4) 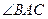 , 5) уравнение прямой, проходящей через точку В параллельную АС.
, 5) уравнение прямой, проходящей через точку В параллельную АС. вектору
вектору 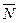
 +z-1=0, x+y
+z-1=0, x+y 


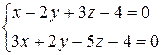 д)
д) 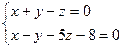
 б)
б)  в)
в)  г)
г) 

 и
и 
 и
и 

 и
и 
 и
и 
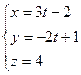 г)
г)  и
и 












 и 2x-y+z+3=0
и 2x-y+z+3=0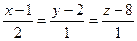
















 а, ВС = 4(β а – b), CD = -4β b, DA = а +α b. Найдите α и β и докажите коллинеарность ВС и DA.
а, ВС = 4(β а – b), CD = -4β b, DA = а +α b. Найдите α и β и докажите коллинеарность ВС и DA.









