
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Методика опрацювання нового матеріалу
Дата добавления: 2014-10-22; просмотров: 5207
|
|
Характер навчально-пізнавальної діяльності учнів у процесі опрацювання нового матеріалу визначає такі його структурні елементи: постановка й усвідомлення учнями пізнавального завдання; сприймання навчального матеріалу; осмислення навчального матеріалу і засвоєння основної його інформації.
Відповідно до цього в опрацюванні нового матеріалу виділяють такі компоненти: підготовка до вивчення нового матеріалу, вивчення нового матеріалу і первинне закріплення.
Підготовка до вивчення нового матеріалу
У вивченні нового матеріалу істотне значення має актуалізація опорних знань. Без повного й глибокого відтворення потрібних знань і вмінь важко добитися активності і певної самостійності учнів класу під час пояснення нового матеріалу. В широкому розумінні підготовчий етап передбачає такі завдання:
а) відтворення опорних знань та деяких прийомів пізнавальної діяльності, окремих загальних умінь чи вмінь виконувати розумові операції (актуалізація знань);
Методика викладання математики в початкових класах 61
б) уточнення чуттєвого досвіду дітей і уявлення про термін відповідно до наукового розуміння поняття;
в) повідомлення теми і мотивування нового матеріалу.
Підготовка до вивчення нового матеріалу проводиться переважно у процесі виконання учнями системи вправ. Добираючи такі вправи, вчитель має ііраховувати особливості нового матеріалу: теоретичні знання (поняття, закономірності), нові випадки усних або письмових обчислень, розв'язу-пання задач нового виду. Де можливо, бажано створити своєрідну наочну модель нового знання. Нерідко тут допомагає самостійне виконання дітьми операцій над множинами предметів. Наприклад, об'єднання чи поділ предметних множин під час ознайомлення з діями додавання або ділення, поділ смужки на рівні частини під час ознайомлення з дробами, зв'язування паличок у пучки-десятки в процесі вивчення нумерації чисел першої сотні.
Особливістю процесу актуалізації в початкових класах є те, що опорні знання й уміння треба не просто нагадати, а й застосувати на практиці. Отже, актуалізація знань має бути ґрунтовною. У процесі актуалізації потрібних знань і вмінь необхідно створити в класі відповідний морально-емоційний клімат, забезпечити високий рівень уваги учнів.
Підготовка матеріалів для актуалізації знань учнів починається з аналізу нового матеріалу, в процесі якого потрібно з'ясувати, які старі (попередні) знання є складовою, частиною нових або основою для їх вивчення.
Розкриємо сутність аналізу на прикладі двох тем.
Тема "Складання таблиці ділення на 2".
Таблиці ділення складають на основі таблиць множення.
У порядку підготовки учні складають приклади на ділення з прикладів на множення. Перед складанням таблиці ділення на 2 бажано прочитати таблицю множення числа 2.
Тема "Множення суми на число".
Для підготовки до сприймання нового матеріалу та повідомлення теми проаналізуємо розв'язання задачі.
Задача. Дівчинка складала букети. Для кожного букета вона брала 3 білі і 2 червоні гвоздики. Скільки всього гвоздик у 7 букетах?
Розв 'язання
Перший спосіб Другий спосіб
(3 + 2) ■ 7 = 35 (гв.). З • 7 + 2 • 7 = 35 (гв.).
Відповідь. 35 гвоздик. Відповідь. 35 гвоздик.
Бесіда. Про що дізнаємося кожною дією під час розв'язування задачі першим способом? (У виразі (3 + 2) • 7 — дві дії. Першою дією дізнаємося, скільки гвоздик її одному букеті, а другою — скільки гвоздик у 7 букетах). Про що дізнаємося кожною дією під час розв'язування задачі другим способом? (У виразі 3-7 + 2-7 — •іри дії. Першою дією дізнаємося, скільки білих гвоздик у 7 букетах, а другою (в порядку виконання) — скільки червоних гвоздик у 7 букетах. Останньою, третьою, дією дізнаємося, скільки всього гвоздик у 7 букетах). Одну й ту саму кількість гвоздик ми знаходимо за допомогою двох виразів. У першому треба було суму чисел 3 і 2 помножити на 7; у другому — кожне з чисел 3 і 2 окремо помножити на62
Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 62 7, а потім знайти суму цих двох добутків. Отже, добуток суми і числа можна знаходити по-різному.
Підготовка до вивчення нового матеріалу завершується оголошенням нової теми і мотивуванням нового матеріалу. Мотивування нового матеріалу — це засіб виховання в дітей позитивного ставлення до навчальної діяльності, зокрема пізнавальних мотивів, інтересу до знань і до самого процесу навчання. На етапі підготовки учнів до сприймання нового матеріалу вчитель розповідає їм про місце нових знань у системі початкового курсу математики, про їх значення для подальшого навчання і трудової діяльності. Отже, мотивування знань тісно пов'язане з формулюванням мети і теми заняття.
У початкових класах тему і мету уроку (тему нового матеріалу) краще повідомляти не на початку заняття, а під час переходу до вивчення нового матеріалу. Бажано робити це різними способами і за можливості з проблемним підходом. Учитель створює проблемну ситуацію, яку учні не можуть розв'язати, оскільки немає потрібних знань, але інтерес до теми виникає.
Вивчення нового матеріалу
Методика вивчення нового матеріалу розкривається у відповідних розділах. Тому ми тут сформулюємо деякі загальні вимоги щодо опрацювання нового матеріалу.
Вибір методів для засвоєння учнями того чи іншого матеріалу залежить від мети навчання, змісту навчального предмета, особливостей мислительної діяльності дітей і від рівня здобутих ними раніше знань, умінь і навичок. Конкретно предметом методики викладання математики є: по-перше, дослідження можливостей реалізації розроблених дидактикою загальних методів навчання математики (потрібно конкретизувати і модифікувати загальні методи навчання з урахуванням специфіки математики); по-друге, доповнення системи загальних методів спеціальними методами навчання, що відображають основні методи пізнання, які застосовуються в математиці.
Відразу зазначимо, що перед методикою викладання математики в початкових класах стоїть тільки перше завдання. Потреба в доповненні ще не набуває актуальності. Вивчення математики в початкових класах достатньою мірою забезпечується на основі реалізації загальних методів. Потрібно лише визначити, якими саме методами вивчати новий математичний матеріал та висвітлити методику їх застосування. Щоб з'ясувати, які із загальнодидактичних методів навчання застосовують для ознайомлення з новим матеріалом на уроках математики, розглянемо їх означення і класифікацію.
Методи навчання найчастіше визначають як упорядковані способи взаємопов'язаної діяльності вчителя й учнів, спрямованої на виконання навчально-виховних завдань. При такому підході наголошується на єдності дій учня і вчителя.
Методи навчання — складне педагогічне явище, в якому можна виділити різні педагогічні аспекти. Тому нема єдиної основи класифікації методів. Здебільшого розглядають три її різновиди: на основі зовнішніх форм прояву
Методика викладання математики в початкових класах 63
методів навчання, за внутрішньою психологічною структурою методів і за логічним засвоєнням знань учнями.
Класифікація на основі зовнішніх форм прояву методів навчання. При цьому враховуються джерела, з яких діти набувають знань. Такими джерелами є: словесна (слухова) форма подання навчальної інформації вчителем і усна форма відтворення знань учнями; зорова форма подання інформації за допомогою наочності; дидактичні завдання або практичні роботи, які виконують учні під керівництвом учителя для одержання нової інформації. Зовнішня форма прояву методів навчання характеризується насамперед їх пояснювально-ілюстративною інформаційною функцією. Вона реалізується словесними, наочними і практичними методами навчання.
Внутрішня психологічна структура методу характеризує рівень пізнавальної активності і самостійності учнів. З точки зору психології у визначенні методів навчання виділяють два підходи — репродуктивний і продуктивний. Нові знання репродуктивними методами засвоюються в результаті виконання дій за зразком. Продуктивне засвоєння знань передбачає розв'язання учнями проблем і проблемних ситуацій, застосування знань у нестандартних умовах. Однак в діяльності вчителя і дітей на уроці репродуктивний і продуктивний методи доповнюють один одного, активно взаємодіють.
Педагогічною формою подолання навчально-пізнавальних суперечностей є проблемність у навчанні. Процес проблемного навчання може здійснюватися на різних рівнях. Здебільшого виділяють три рівні і, відповідно, три методи навчання: метод інформаційно-проблемного викладу знань; частково-пошуковий метод (учнів залучають до розв'язування проблеми лише на окремих етапах); дослідницький метод (проблемну ситуацію створює вчитель, але розв'язують її учні в процесі самостійної діяльності). Останній метод ми надалі називатимемо самостійно-пошуковим, оскільки дослідницький метод в літературі для вчителів початкових класів часто пов'язували з проведенням дослідів на уроках природознавства.
Класифікація на основі логічного засвоєння знань. Вона характеризується формами і прийомами мислення і враховує методи теорії пізнання. Серед способів керування навчанням є специфічні способи висвітлення змісту нового матеріалу вчителем, розраховані на те, щоб викликати ту чи іншу форму мислення. Залежно від основного значення того чи іншого логічного прийому визначають такі логічні методи пізнання: аналітико-синтетичні (аналітичний, синтетичний, аналітико-синтетичний), індуктивно-дедуктивні (індуктивний, дедуктивний, індуктивно-дедуктивний), метод порівняння, метод аналогії.
У процесі аналізу ми йдемо від невідомого до відомого, від шуканого до даного (зворотним шляхом), а в процесі синтезу — від відомого до невідомого, від даних до шуканого (прямим шляхом). У цьому розумінні аналіз і синтез мають велике значення в розв'язуванні задач.
Якщо умовивід зроблено в результаті спостережень кількох окремих однотипних властивостей, то таку форму розумової діяльності, спрямовану на узагальнення, називають індукцією. Якщо при цьому індукція
Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 64
здійснюється за допомогою евристичної бесіди, то таку бесіду називатимемо евристично-індуктивною бесідою.
Дедукція — це умовивід, що є застосуванням раніше встановленого загального положення до окремого випадку. Якщо дедукція здійснюється на основі евристичної бесіди, то таку бесіду називатимемо евристично-дедуктивною. (Зауважимо, що дедукція може бути формою викладу матеріалу в підручнику, зумовленою аксіоматичним методом).
Аналогія в навчанні — це спосіб засвоєння нової інформації на основі встановлення подібності між об'єктами. Аналогію розуміють як такий умовивід, коли на основі подібності двох об'єктів за деякими ознаками і наявності додаткової ознаки в одному з них роблять висновок про наявність такої самої ознаки і в іншому об'єкті. У початкових класах аналогія застосовується на основі бесіди, тому ведуть мову про бесіду із застосуванням прийому аналогії.
Метод порівняння в процесі пояснення нового матеріалу з математики розглядається як прийом, що супроводжує різні методи вивчення нового матеріалу.
Розглянемо застосування загальнодидактичних методів на уроках математики в початкових класах для вивчення нового матеріалу. При цьому враховуватимемо зв'язки між методом навчання і навчальним прийомом. Метод охоплює всю навчальну роботу, а прийом — тільки окремі разові дії.
Перед тим як подати єдиний (лінійний) перелік методів, що застосовуються на етапі пояснення нового матеріалу, порівняємо евристичну бесіду і частково пошуковий метод. За ступенем активності учнів вони рівнозначні. Близькі вони і за своєю сутністю. Тому вважатимемо, що частково-пошуковий метод реалізується в евристично-дедуктивній або евристично-індуктивній бесідах.
Методи, запропоновані для ознайомлення з новим матеріалом, подамо у порядку підвищення активності пізнавальної діяльності учнів: 1) розповідь; 2) пояснення; 3) метод проблемного викладу знань учителем; 4) репродуктивна бесіда; 5) бесіда із застосуванням прийому аналогії; 6) евристично-дедуктивна бесіда; 7) евристично-індуктивна бесіда; 8) експериментально-практичний метод; 9) самостійна робота учнів з підручником; 10) самостійно-пошуковий метод.
Традиційно перших три методи належать до методу усного (зв'язного) викладу, четвертий — сьомий до методу бесіди, восьмий — до практичних методів і дев'ятий та десятий — до методу самостійної роботи.
Метод усного монологічного викладу застосовується для ознайомлення учнів з правильною математичною мовою та для навчання слухати і розуміти її; для подання зразків пояснення прийомів обчислень і розв'язування задач; формування вмінь давати пояснення матеріалу у вигляді зв'язної розповіді.
Методи усного викладу здебільшого використовують у процесі ознайомлення з: деякими загальними математичними поняттями (десяткова система числення; принцип усної і письмової систем нумерації; метричні системи мір; арифметичні дії; таблиці арифметичних дій; поняття математичного
Методика викладання математики в початкових класах 65
виразу, рівняння, геометричні фігури тощо); теоретичними відомостями (правила порядку виконання арифметичних дій; математичні терміни, відомості з історії математики); окремими прийомами обчислень (множення на 1 та 0; ділення на 1; алгоритми письмового виконання арифметичних дій); окремими видами нових задач (вибірково); будовою та інструкцією використання інструментів і вимірювальних приладів (лінійка, циркуль, терези, палетка).
Учитель повідомляє учням готові знання, пояснює і доводить їх істинність. На основі безпосереднього спостереження предметних множин, чисел, математичних записів чи відповідних наочних об'єктів він узагальнює окремі дані, робить загальний висновок. Учитель подає зразки прийомів практичної діяльності і мотивує їх доцільність, організовує заучування навчального матеріалу спеціальними прийомами. Перед учнями не ставиться завдання самостійно знайти відповідь. Вони мають уважно слухати, намагаючись зрозуміти й осмислено запам'ятати матеріал. На основі пояснення матеріалу діти оперують готовими знаннями в межах репродуктивної пізнавальної діяльності: усне відтворення усвідомлених знань, застосування правил для виконання вправ і задач.
Діалогічна форма пояснення (бесіда) активізує діяльність дітей, розвиває в них уміння спостерігати й аналізувати математичні явища, робити узагальнення, підводити окреме під загальне. Вона є важливим засобом організації колективної роботи на уроці та індивідуального підходу до учнів. Така форма пояснення нового матеріалу найбільше відповідає віковим особливостям молодших школярів.
Метод бесіди застосовується для ознайомлення із: закономірностями (властивості арифметичних дій; взаємозв'язки між математичними поняттями, зв'язки між компонентами і результатами арифметичних дій, пропорційна залежність між величинами); знаннями практичного характеру, що вводяться на основі теоретичних знань (обчислювальні прийоми, прийоми розв'язування рівнянь, знаходження числових значень величин за відомими формулами); задачами нового виду.
Учитель сам планує етапи розв'язування проблеми, а учень осмислює проблему і за пропозицією вчителя бере участь у виконанні окремих її етапів. Отже, вчитель формулює запитання і визначає їх послідовність, стежить за відповідями учнів, уточнює їх, підбиває підсумки бесіди і формулює її висновки. Учні вникають у запитання, пригадують потрібний для відповідей матеріал, відповідають на запитання, осмислюють висновки та узагальнення. Якщо за допомогою бесіди вчитель підводить учнів до самостійних висновків, то таку бесіду називають евристичною.
Запитання, що ставляться в ході бесіди, за їхніми функціями можна поділити на три групи:
— репродуктивно-мнемонічні запитання, що активізують лише роботу пам'яті і спрямовані на відтворення або закріплення раніше вивченого;
— репродуктивно-пізнавальні запитання, що стимулюють репродуктивну пізнавальну діяльність, спрямовану на розв'язування задач раніше
Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 66
— продуктивно-пізнавальні запитання, що стимулюють пошукову пізнавальну діяльність учнів і дають їм істотно нові знання.
Перша група завдань відтворює діалог учителя й учнів, коли основні повідомлення робить сам учитель. Це — бесіда-пояснення, або репродуктивна бесіда. Друга і третя групи завдань реалізуються на основі бесіди евристичного характеру. Для другої групи завдань характерний дедуктивний хід бесіди, а для третьої — індуктивний.
Експериментально-практичний метод застосовується тоді, коли можна легко зробити предметну (наочну) модель математичної проблеми чи застосувати вимірювання.
Самостійна робота як метод опрацювання нового матеріалу може застосовуватись для різного виду математичних знань. Проте в початкових класах на етапі опрацювання нового матеріалу вона важлива насамперед для розвитку вмінь самостійно працювати.
Розглянемо застосування кожного із зазначених методів для ознайомлення з новим матеріалом.
Розповідь. Усний виклад матеріалу у вигляді розповіді характеризується конкретністю, образністю, доступністю, стислістю, динамічністю. Після розповіді вчитель пропонує учням повторити зміст нового матеріалу за запитаннями. Якщо учні не можуть відповісти на запитання, то вчитель проводить додаткове пояснення.
Тема "Усне додавання трицифрових чисел виду 520 + 340". Розповідь проводиться за таким записом:
520 + 340 = ______
/\ /\
500 + 20 300 + 40
500 + 300 = 800
20 + 40 = 60
800 + 60 = 860
520 + 340 = 860
Потрібно знайти суму чисел 520 і 340. Із запису видно, що кожний доданок розкладено на сотні і десятки. Окремо додають сотні (500 + 300 = 800) і десятки (20 + 40 = 60). Додавши знайдені числа (800 + 60 = 860), отримали відповідь. Отже, можна зробити висновок, що при додаванні сотні додають до сотень, десятки — до десятків.
При додаванні трицифрових чисел ми користувалися переставною властивістю. Розглянемо іншу форму розгорнутого запису дії додавання:
450 + 230 = 400 + 50 + 200 + 30 = 400 + 200 + 50 + ЗО = 600 + 80 = 680. Користуючись записом, пояснити, як знайшли суму чисел 450 і 230.
Пояснення — ускладнений вид розповіді, що характеризується доказовістю твердження. Пояснюючи, вчитель звертається із запитанням до учнів класу, пропонує розв'язати нові приклади і задачі на застосування нових понять, правил чи прийомів.
Методика викладання математики в початкових класах 67
Тема "Задачі на порівняння продуктивності праці".
Задача. Дві ланки учнів допомагали збирати смородину. В першій ланці було чотири учні, а в другій — 5. Перша ланка зібрала 24 кг ягід, а друга — 25 кг. Яка ланка працювала краще?
Пояснення. У задачі треба визначити, яка ланка працювала краще. Для цього необхідно знайти, скільки кілограмів ягід зібрав кожен учень у першій ланці і скільки — в другій. Відомо, що в першій ланці 4 учні, а зібрали 24 кг ягід. За цими даними можна дізнатися, скільки ягід зібрав один учень. Для цього поділимо 24 на 4. Як знайти, скільки кілограмів ягід зібрав один учень у другій ланці? Запишемо потрібні вирази і виконаємо дії:
1) 24 : 4 = 6 (кг) смородини зібрав один учень першої ланки;
2) 25 : 5 = 5 (кг) смородини зібрав один учень другої ланки.
Чи можна тепер дати відповідь на запитання? (Так, краще працювали учні першої ланки).
Проблемний виклад знань. Проблемне пояснення в початкових класах полягає в тому, що вчитель сам ставить проблему і сам її вирішує. Учням пропонується зразок вирішення проблеми, пояснюється хід думки. Діти стежать за логікою пояснення, засвоюють окремі етапи розв'язання проблеми або цілісний розв'язок. Однак учитель не тільки стверджує наукові істини, а немовби залучає слухачів до дослідження проблеми.
Коли вчитель вдається до проблемного викладу матеріалу, активність учнів дещо зростає порівняно з уроками, на яких застосовуються методи розповіді і пояснення. Проілюструємо це на прикладі опрацювання однієї й тієї самої теми "Позатабличне ділення виду 42 : 3" різними методами.
Тема "Позатабличне ділення виду 42 : З".
Розповідь. Щоб поділити число 42 на 3, треба замінити число 42 сумою таких шюх доданків, кожний з яких можна поділити на 3, а потім застосувати відоме правило ділення суми на число. У даному разі зручно записати число 42 у вигляді пуми (30 + 12). 30 поділимо на 3, отримаємо 10; 12 поділити на 3, буде 4. Разом 14. Хід міркування можна записати так:
42 : 3 = (ЗО + 12) : 3 = 30 : 3 + 12 : 3 = 10 + 4 = 14.
Пояснення. Ми навчилися ділити двоцифрові числа на одноцифрові для випадків, коли кожний розряд діленого ділиться на дільник. Наприклад:
46 : 2 = (40 + 6) : 2 = 40 : 2 + + 6 : 2 = 20 + 3 = 23.
Розглянемо складніший випадок. Треба поділити 42 на 3. Спробуємо застосувати нідомий прийом: замінимо 42 сумою його розрядних доданків (40 + 2). Однак ні 40, іі 2 не ділиться на 3. Отже, прийом розкладання на розрядні доданки не підходить. Спробуємо знайти інший підхід до розв'язування. Утворимо число 42 з пучків-іесятків і з окремих паличок. 4 десятки на 3 не діляться, але на 3 рівні частини иожна поділити 3 десятки. Розкладемо 42 на доданки 30 і 12. 30 поділити на 3, буде 10; 12 поділити на 3, буде 4. Разом 14.
Як же можна поділити 42 на 3? Спочатку беремо з цього числа стільки десятків, цоб їх число ділилося на 3, а потім ділимо решту одиниць. У такому разі число юзкладається не на розрядні доданки, а на зручні. Хід міркування можна записати пік:
42 : 3 = (ЗО + 12) : 3 =30 : 3 + 12 : 3 = 10 + 4 = 14.
Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 68
Проблемний виклад. Нам треба поділити 42 на 3. Спробуємо замінити число 42 сумою його розрядних доданків (40 + 2). Однак ні 40, ні 2 не ділиться на 3.
Чи не можна подати число 42 у вигляді суми будь-яких інших доданків, але таких, щоб кожний з них ділився на 3? Спробуємо це зробити. Числа братимемо з таблиці множення числа 3. (Учні випробовують числа 15 і 27, 18 і 24, 21 і 21, 30 і 12). Найзручніший варіант — розкладання числа на 30 і 12.
З трьох варіантів викладу одного й того самого навчального матеріалу видно, як змінюється пізнавальна активність дітей. У першому варіанті їм потрібно зрозуміти та запам'ятати подане пояснення, у другому — шукати новий прийом, а в третьому — ознайомитися не тільки з новим прийомом обчислення, а й з тими запитаннями, які виникають під час розв'язування нової задачі.
Репродуктивна бесіда. Така бесіда близька до розглянутого вже методу пояснення. Проводиться вона за певним планом. Запитання за характером здебільшого риторичні або навідні.
Тема "Множення двоцифрового числа на двоцифрове". Бесіда. Розв'яжемо задачу.
Задача. Школа купила 36 спортивних костюмів по 24 грн. кожний. Визначити вартість покупки.
Яку дію треба виконати, щоб знайти відповідь задачі? (Дію множення: 24 помножити на 36). Як виконати обчислення усним способом?
24 ■ 36 = 24 ■ (30 + 6) = 24 • 30 + 24 • 6 = 720 + 144 = 864 (грн.). Як можна записати проміжні обчислення письмовим способом? 24 24 144
Х6 х 30 + 720
144 720 864
Ці окремі дії можна подати в єдиному запису. Множники записують один під одним. Спочатку множимо 24 на 6 одиниць, потім 24 множимо на 3 десятки і знайдені числа додаємо. Учитель подає пояснення множення і пропонує учням повторити його.
Х 36
Тема "Задачі на три дії, що включають два рази операцію зменшення або збільшення числа на кілька одиниць чи в кілька разів".
Задача. Коневі на день дають 16 кг сіна, кормових буряків — у 2 рази менше, ніж сіна, а вівса — у 4 рази менше, ніж: буряків. Скільки кілограмів кормів дають коневі на день?
Сіна — 16 кг.
Буряків — у 2 рази менше, ніж сіна.
Вівса — у 4 рази менше, ніж буряків.
Після ознайомлення зі змістом задачі вчитель повідомляє, що задачу слід аналізувати від числових даних.
Методика викладання математики в початкових класах 69
Коневі давали сіно, буряки й овес. Треба знайти, скільки кілограмів буряків згодовували коневі на день. Із задачі вже відомо, що ча день коневі видавали 16 кг сіна.
Що відомо про буряки? Як знайти, скільки кілограмів буряків давали коневі? (Буряків давали в 2 рази менше, ніж сіна. Щоб знайти, скільки кілограмів буряків давали коневі, треба 16 поділити на 2).
Що відомо про овес? Як дізнатися, скільки кілограмів вівса давали коневі? (Вівса давали в 4 рази менше, ніж буряків. Щоб знайти, скільки кілограмів вівса давали коневі, треба число кілограмів буряків поділити на 4).
Розповісти повністю план розв'язування задачі. Записати розв'язання в зошит.
Підсумовуючи роботу над задачею, учитель звертає увагу на те, що під час її розв'язування їм довелося два рази зменшувати число в кілька разів.
Бесіда із застосуванням прийому аналогії. В умовиводах за аналогією думка формується від одиничного до одиничного. В результаті цього знання переносяться з раніше вивченого об'єкта на інший, менш вивчений.
Тема "Усне додавання трицифрових чисел без переходу через розряд".
Бесіда. Ми вміємо додавати двоцифрові числа. Поясніть прийом додавання, користуючись розгорнутим записом:
26 + 43 = (20 + 6) + (40 + 3) = (20 + 40) + (6 + 3) = 60 + 9 = 69.
Подумайте, чи можна таким способом знайти суму трицифрових чисел 243 і 321 (учитель не показує розгорнутого запису). Скільки чисел додавали у першому прикладі? Як записували числа у першому прикладі? Які доданки додавали? Спробуйте іробити так само і при додаванні трицифрових чисел.
Евристично-дедуктивна бесіда. Застосовуючи евристично-дедуктивну бесіду, вчитель повідомляє загальне положення, а потім за допомогою запитань спрямовує учнів до з'ясування конкретних прикладів.
Тема "Розв'язування рівнянь на знаходження невідомого множника".
Підготовка та пояснення нового матеріалу. Прочитайте приклад: 6 ■ 3 = 18. Поділіть добуток на один із множників. Що ви помітили? Що отримали, коли добуток поділили па один із множників? (Учні повторюють правило знаходження невідомого множника). Знайти невідомий множник у прикладі: Ц ■ 3 = 15.
Задача. Невідоме число помножили на 4 й отримали 28. Знайти невідоме число.
Для розв'язування задачі позначимо невідоме число буквою х. Як тепер можна записати задачу? (Можна скласти рівняння: х ■ 4 = 28). Що відомо в цьому рівнянні? ІЦо невідомо? Як знайти невідомий множник?
Запишемо розв'язання рівняння і відповідь задачі: х = 28 : 4
Відповідь. Невідоме число дорівнює 7.
Евристично-індуктивна бесіда. Сутність евристично-індуктивної бесіди полягає в тому, що вчитель спочатку пропонує розглянути конкретні приклади (однотипні). На основі їх аналізу учні доходять загального висновку.
Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 70 Тема "Переставна властивість додавання".
 
| 1 2 4 |
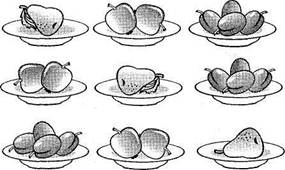
| 1+2+4=7 2+1+4=7 4+2+1=7 |
Мал. 25
Бесіда. На малюнку три групи предметів (1 груша, 2 яблука і 4 сливи). У кожному рядку ці предмети розміщені по-різному. За малюнком складено такі приклади: 1+2+4 2+1+4 4+2+1
Додати числа в кожному рядку і записати відповіді. Що однакового в прикладах? Чим відрізняються ці приклади між собою?
Обчислити ще такі суми: 5 + 3 і 3 + 5. Чи зміниться результат додавання, коли змінити порядок додавання чисел? Який з цього можна зробити висновок? (Додавати числа можна в будь-якому порядку).
Експериментально-практичний метод. За експериментально-практичним методом істинність нових знань стверджують зіставленням їх з реальною дійсністю. Застосування способу починається зі створення конкретного або уявного образу ситуації, що розглядається. Робота проводиться у вигляді інструктажу,
Тема "Розподільна властивість множення".
Опрацювання нового матеріалу. Вчитель пропонує учням покласти в один ряд 5 чорних і 2 білих кружечки, а потім викласти ще два таких самих ряди (мал. 26).

Мал. 26
Методика викладання математики в початкових класах 71
Спираючись на модель, знайдіть два способи обчислення кількості всіх кружечків. Потрібно скласти вирази. Обчислювати значення виразів не треба.
Учитель дає завдання учням обчислити такі вирізи:
(5 + 2) • 3 і 5 • 3 + 2 • 3.
Учні коментують, що означає кожна дія і що означає кожний вираз загалом.
Обидва вирази означають, скільки всього кружечків. Отже, значення виразів рівні. Можна записати так:
(5 + 2) • 3 = 5 • 3 + 2 • 3.
На основі аналізу рівності роблять висновок про те, що множити суму на число можна двома способами.
Самостійна робота учнів з підручником. Підручник — важливе джерело знань, тому вчитель має навчити учнів користуватися ним. Працюючи над підручником, діти вчаться сприймати математичний текст, розглядати малюнки, схеми, структурні записи; робити спочатку під керівництвом учителя, а потім і самостійно висновки, узагальнення. Робота з підручником сприяє розвитку математичного мислення, самостійності, інтересу до вивчення математики.
Значна частина матеріалу в підручнику з математики призначена для самостійної роботи в класі та вдома. Це репродуктивна робота на виконання обчислень та розв'язування задач. У діючих підручниках початкової школи у багатьох випадках подано повне пояснення нового матеріалу. Реалізується пояснення здебільшого за допомогою системи вправ. На основі виконаних прикладів діти роблять узагальнення. Рівень пізнавальної активності варіюється в широкому діапазоні: від здобування знань у готовому вигляді до здобування їх на основі дослідницької роботи.
Тема "Задачі на дворазове збільшення в кілька разів одиничного значення величини".
Задача. За годину роботи трактор витрачає 8 л пального. Скільки літрів пального потрібно для 5 таких тракторів на 10 год роботи ?
План розв'язування
1. Скільки літрів пального потрібно для 5 тракторів на 1 год?
2. Скільки літрів пального потрібно для 5 тракторів на 10 год?
Завдання: а) проаналізувати задачу й усно розв'язати її за поданим планом; б) самостійно скласти і розв'язати подібну задачу.
Перевірка правильності виконання самостійної роботи буде водночас прийомом первинного закріплення.
Самостійно-пошуковий метод. Самостійно-пошуковий метод, що застосовується в початкових класах, — це невеликі пошукові задачі, які розкривають основні етапи процесу дослідження: спостереження і вивчення математичних фактів, з'ясування незрозумілих явищ, котрі потрібно дослідити, висунення гіпотези (припущення), складання плану дослідження та його здійснення, формулювання висновку.
Самостійно-пошуковим методом можна вивчати математичні закономірності, способи виконання дій, правила й формули, пов'язані з деякими конкретними знаннями дітей.
Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 72
На додаток до розглянутих методів подамо ще коротке повідомлення про метод програмованого навчання, що набув певного поширення в 70-х роках XX століття. Його суть полягає в тому, що навчальний матеріал розподіляють на невеликі частини (кадри). Ознайомившись з матеріалом першого кадру і продумавши його, учень для самоконтролю дає відповідь на одне або кілька запитань, виконує вправу. Переконавшись у правильності відповіді, він працює над завданнями наступного кадру.
Методом програмованого навчання кожний учень вивчає матеріал індивідуально, за своїм темпом, виявляючи при цьому найбільший ступінь самостійності. Отже, використання деяких прийомів програмованого навчання доцільне. Його можна практикувати на основі дозування матеріалу підручника.
Застосовуючи той чи інший метод пояснення нового матеріалу, треба зважати на закономірності інформаційних процесів у психіці. Збільшення інформації посилює активність учнів, підвищує надійність сприйняття інформації. Отже, чим більше сигналів (зорових, слухових, дотикових тощо) надходить ззовні і чим більше органів чуття залучено до прийняття інформації, тим швидше й точніше відбувається сприймання. Однак , перевантаження органів сприймання повідомленнями уповільнює їх прийом і осмислення. Заважають сприймати нову інформацію і так звані шуми. У навчанні до них належать повторення відомого, яке нічого нового не містить, зайва деталізація, непотрібні відомості. Усунення шуму приховує в собі значні резерви для підвищення ефективності навчання.
Засвоєння знань охоплює і засвоєння інформації про способи дії. Щоб засвоїти способи діяльності, учень має багато разів застосовувати знання і навички у схожій ситуації, він повинен відтворювати їх. Треба, щоб цей спосіб став досконалим умінням, а його елементи — навичками.
Первинне закріплення
Первинне закріплення йде після пояснення нового матеріалу і здійснюється під безпосереднім керівництвом учителя. Основна його мета полягає в тому, щоб дізнатися, чи зрозуміли діти новий матеріал, і показати, як його застосовувати. Первинне закріплення здебільшого охоплює пряме відтворення виучуваного матеріалу та коментоване розв'язування математичних завдань. За методикою організації воно істотно залежить від методів пояснення нового матеріалу. Якщо для пояснення застосовувалась розповідь, то для відтворення краще скористатися бесідою. Коли вчитель пояснює за допомогою евристичної бесіди, для первинного закріплення можна організувати читання матеріалу підручника.
Щоб учні краще осмислили новий матеріал на етапі первинного закріплення, потрібно розчленовувати інформацію на невеликі частини, подавати зразки розв'язання прикладів і задач.
Одна з форм роботи — розв'язування задач і вправ, коли один учень працює біля дошки (і часто виконує завдання з коментуванням), а решта робить відповідні записи в своїх зошитах. Нерідко практикується коментований розбір вправ з подальшим розв'язуванням їх на дошці.
Методика викладання математики в початкових класах 73
Зауважимо, що коментоване розв'язування вправ — нелегка справа. Адже, щоб дати пояснення, треба не тільки знати правила, а.й уміти їх застосовувати. Тому при первинному закріпленні спочатку коментує вчитель, потім — сильніші учні, після цього — хто бажає і за викликом. Зрозуміло, що в цьому виникає потреба тоді, коли клас зовсім немає відповідних навичок.
Основна мета коментованого розв'язування вправ — довести знання учнів до повного усвідомлення, озброїти школярів способами виконання певних дій.
Тема "Розв'язування задач способом відношення" (4 клас). Первинне закріплення. 1. Розглянемо одну з розв'язаних задач. Задача. На пошиття трьох чоловічих костюмів витрачено 8 м тканини. Скільки метрів тканини потрібно на 12 таких костюмів?
З к. — 8 м. 12 к. - ?
Бесіда. Більше чи менше потрібно тканини на 12 костюмів, ніж на 3 костюми? Як дізнатися, у скільки разів більше потрібно тканини на 12 костюмів, ніж на З? Розгляньте розв'язання і поясніть, про що дізнавалися кожною дією:
1) 12 : 3 = 4 (рази);
2) 8 • 4 = 32 (м).
2. Складіть подібну задачу, знаючи, що на 2 сорочки потрібно 5 м тканини. Як видно, первинне закріплення вже охоплює елементи самостійних повідомлень учнів. Тому за ним здебільшого йде самостійна робота всього класу.
§14. Закріплення й узагальнення знань учнів
Розглянемо організацію навчальної діяльності учнів на останньому етапі комбінованого уроку, що охоплює закріплення і повторення, повідомлення домашньої роботи та підсумок уроку. В кожній з цих складових можуть бути елементи узагальнення.
На закріплення матеріалу не слід шкодувати часу. В середньому на цей пап уроку відводиться 15 хв. Важливо забезпечити максимальний вияв самостійності учнів. Для цього створюють різні ситуації щодо застосування шань, нові знання розглядаються в різних аспектах. Під час закріплення пдаються до конкретизації та узагальнення, порівняння, класифікації, і'ясування причинно-наслідкових зв'язків.
На етапі закріплення застосовуються знання під час фронтального ииконання різного роду навчальних завдань (під безпосереднім керівництвом учителя) та самостійної роботи.
При визначенні змісту повторення треба враховувати вимоги до знань, умінь і навичок на кінець навчання в кожному класі. Зважаючи на наявність дидактичних матеріалів, учитель уточнює зміст роботи, варіює завдання, мігшачає форму їх виконання (фронтальна, колективно-групова, індивідуальнії), способи диференційованого підходу до учнів з різною успішністю, засоби шоротного зв'язку тощо.
Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 74
Розглянемо організацію навчальної діяльності дітей за матеріалами підручника, індивідуальних карток та зошитів з друкованою основою. В організації роботи максимальну увагу треба приділити диференційованому підходу.
Робота за підручником та записами на дошці. Організацію навчальної роботи учнів будемо описувати одночасно з розкриттям різних способів диференційованого підходу.
Перший спосіб. Завдання для самостійної роботи пропонуються в одному чи двох варіантах. Для учнів, які виконають роботу раніше від інших, пропонуються додаткові завдання. Учитель записує їх на дошці або на окремих картках.
Додаткові завдання — це здебільшого завдання з логічним навантаженням. Невиконання учнем додаткових завдань не впливає на його оцінку в балах. Робота над ними оцінюється словесно і, як правило, в позитивному плані. Додаткові завдання можуть бути не тільки для сильних, а й для інших учнів. Вони мають бути цікаві, але неважкі. Такі варіанти зовні менше відрізняються один від одного, а отже, менш помітний поділ учнів на групи за успішністю. Наведемо приклад.
Тема (закріплення) "Віднімання двоцифрових чисел без переходу через десяток". Завдання для самостійної роботи. Знайдіть значення виразів (за підручником). 100 – 100-1 99-12 20 + 80 54 - 21
33 -3 30-1 87-33 29-9
Додаткове завдання. З поданих виразів обчисліть ті, які зможете:
23 + 49 87 - 29 33 + 33 75 - 15
Другий спосіб. Завдання для самостійної роботи добирають у двох варіантах, причому в кожному воно підпорядковане одній меті, але одне з них легше.
Тема (закріплення) "Знаходження частини числа".
I варіант. Розв'яжіть задачу (за підручником).
Задача. 1/5 маси картоплі становить крохмаль. Скільки кілограмів крохмалю отримаємо з 375 кг картоплі?
II варіант. Розв'яжіть задачу, записану на дошці.
Задача. У книжці 120 сторінок. Хлопчик прочитав першого дня 1/4 всіх сторінок ' книжки. Скільки сторінок прочитав хлопчик першого дня?
Тут використано прийом заміни числових даних. Для обох варіантів добирають аналогічні задачі як за складністю, так і за спрямуванням. В одній з них числові дані замінюють так, щоб прийоми обчислення в ході розв'язування були на той час ґрунтовно опрацьовані. У такому разі учні зосереджують увагу не на прийомах обчислення, а на зв'язках і відношеннях між величинами, про які йдеться в задачі.
Як спосіб полегшення в одному з варіантів можна повідомити відповіді до задач чи прикладів.
Третій спосіб. Завдання для всіх учнів пропонують в одному варіанті. Диференційований підхід проводять за допомогою відповідного інструктажу.
Тема (закріплення) "Розвиток в учнів умінь розв'язувати задачі, обернені до задач на знаходження суми двох добзптсів".
Методика викладання математики в початкових класах 75
До умови задачі подають 2—3 запитання. Кожному учневі пропонують знайти відповідь на стільки запитань, на скільки він зможе. Зрозуміло, що треба намагатися відповісти на всі запитання.
Умова. З 24 м тканини закрійниця викроїла 6 жіночих і З дитячі сукні. На кожну жіночу сукню вона витратила по 3 м тканини.
Запитання: 1. Скільки всього метрів тканини було витрачено на жіночі сукні? 2. Скільки метрів тканини було витрачено на кожну дитячу сукню? 3. На скільки більше метрів тканини витрачали на одну жіночу сукню, ніж на дитячу?
Четвертий спосіб. Завдання пропонують в одному чи двох варіантах. Слабшим учням надається допомога у вигляді індивідуальних карток.
Способи допомоги є різні: подання зразка розв'язання, плану або схеми розв'язування; інформації, потрібної для виконання завдання; конкретизація завдання; повідомлення початку розв'язання завдання.
Як спосіб диференційованого підходу застосовують також виконання завдань за визначений час. Учням пропонують один або кілька варіантів і зазначають тривалість роботи. Кожний школяр працює в своєму темпі. Для цього зручно давати приклади і задачі, що вже розв'язувались (пропонують відразу кілька задач).
Зауважимо, що повторне розв'язування задач доцільно практикувати частіше, оскільки воно поглиблює знання дітей про вид задачі, сприяє розвитку пам'яті. Повторне пояснення способу розв'язання задачі сприяє розвитку в учнів зв'язного мовлення, закріпленню раніше утворених зв'язків.
Навчальна робота за індивідуальними картками. Робота за індивідуальними картками є поширеною формою організації навчальної діяльності молодших школярів. її практикують на всіх етапах уроку, але здебільшого під час закріплення. За допомогою карток із завданнями неважко здійснювати диференційований підхід: допомагати учням, які повільніше сприймають матеріал, ставити підвищені вимоги до сильних учнів.
В умовах класно-урочної форми навчання програмний матеріал подається одночасно для всіх учнів, тому на уроці в різних варіантах пропонують завдання, що мають спільну пізнавальну мету, але відрізняються ступенем складності чи ступенем допомоги. У ході роботи за картками вчитель індивідуально допомагає тим учням, які звертаються для надання їм допомоги або тривалий час не починають розв'язувати завдання.
Щоб забезпечити чіткість етапів уроку та організований перехід від одного ниду навчальної роботи до іншого, потрібно добитися одночасного завершення роботи над картками всіма учнями класу. Цьому підпорядковано добір додаткових завдань і надання допомоги в ході розв'язування завдань.
Перевіряють правильність виконання завдань та підбивають підсумки самостійної роботи відразу на даному уроці. Форми перевірки такі, як і домашньої роботи. Однак доцільно збільшити роль взаємоперевірки.
Самостійну роботу всіх учнів класу за картками бажано практикувати хоч би раз на тиждень. Для цього використовують дидактичні матеріали. Якщо виникає потреба, то застосовують варіанти серій, які використовують для фронтальної роботи, дублюють.
Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 76
Подамо зразок індивідуальних карток для розв'язування задач на зведення до одиниці та з буквеними даними (перший варіант — полегшений, третій — ускладнений) (3-й клас).
/ варіант
1. 18 л томатного соку розлили порівну в 6 банок. Скільки таких банок потрібно, щоб розлити 12 л соку?
Вказівка. У першій дії треба дізнатися, скільки літрів соку наливали в одну банку.
2. До кожної сукні пришивали 6 ґудзиків. Усього пришили а ґудзиків. До скількох суконь пришили ґудзики? Скласти вираз для розв'язування задачі.
// варіант
1. 48 кг моркви розклали у 8 ящиків порівну в кожний. Скільки потрібно таких ящиків, щоб розкласти 54 кг моркви?
2. Перше число а, а друге — в 5 разів менше. Чому дорівнює друге число? /// варіант
1. За 3 год друкарка надрукувала 12 сторінок. За скільки годин вона надрукує 20 таких сторінок?
Вказівка. Розв'язати задачу окремими діями і складанням виразу.
2. В одному сувої а метрів тканини. Скільки метрів тканини в Отаких сувоях?
3. В Юрка й Оксани було порівну горіхів. Юрко дав Оксані 2 горіхи. На скільки більше горіхів стало в Оксани, ніж у Юрка?
Використання зошита з друкованою основою. Мета використання зошитів з друкованою основою на уроках математики — підвищити ефективність навчальної праці дітей, сприяти вихованню культури математичних записів, забезпечити умови для організації специфічних завдань (сполучити дві точки відрізком, побудувати трикутник за трьома даними точками та ін.).
На етапі закріплення зошити з друкованою основою доцільно використовувати насамперед для узагальнюючого повторення за темою. Розглянемо, наприклад, тему "Додавання двоцифрових чисел без переходу через десяток" (2-й клас).
Тема "Додавання двоцифрових чисел без переходу через десяток".
1. Обчисліть за зразком:
34 + 25 = ЗО + 4 + 20 + 5 = 50 + 9 = 59
55 + 12 = ______________________________________
37 + 62 = ______________________________________
2. 22 + 77 = ____ 36 + 20 = ____
/ \ / \ / \
20 + 2 70 + 7 30 + 6
63 + 4 = ____ 84 + 20 = ____
/ \ / \
60 + 3 80 + 4
Методика викладання математики в початкових класах 77
3.
| Доданок | ||||||||||
| Доданок | ЗО | |||||||||
| Сума |
Учитель пропонує спочатку виконати вправи 1 і 2. Коли більшість дітей впорається із завданням, роботу припиняють (необов'язково розв'язувати всі приклади). Учні мають прокоментувати розв'язання двох прикладів, наприклад: 37 + 62 і 84 + 5. Потім вони самостійно за певний час (2 хв) виконують вправу 3. Кожний працює у своєму темпі, розв'язує стільки прикладів, скільки встигне. Відповіді до прикладів учні читають в порядку їх запису.
| <== предыдущая лекция | | | следующая лекция ==> |
| Ігри та ігрові форми завдань | | | Подання домашнього завдання |