Зміна елементів задачі.

Дата добавления: 2014-10-22; просмотров: 2431

Зміна числових даних. Пропонують розв'язати задачу, аналогічну до розв'язаних на цьому чи попередніх уроках, але з іншими числовими даними. Здебільшого змінюють одне з даних.

Задача. Упертій бригаді 7 сівалок, а в другій — на 2 сівалки менше. Скільки сівалок в обох бригадах?

Завдання:

а) розв'язати таку саму задачу, але щоб в ній було сказано, що в другій бригаді на 4 сівалки більше;

б) розв'язати задачу, але число 7 замінити іншим числом;

в) розв'язати задачу, але числові дані замінити так, щоб шукане число збільшилось.

Виконуючи завдання, учні впевнюються, що задача розв'язується такими самими діями, якими й попередня. Відбувається процес узагальнення способу розв'язування. Це і є головна мета прийому зміни числових даних. У деяких випадках можна запропонувати дітям змінити числові дані так, щоб задачу можна було розв'язати іншим способом.

Методика викладання математики в початкових класах

Зміна запитання. Застосування цього прийому наголошує на спрямовуючій ролі запитання для вибору необхідних зв'язків, стимулює учнів до всебічного аналізу задачної ситуації. Зміну запитання використовують також для постановки нових задач, "розширення" задачі.

Задача. У першій каністрі 18 л бензину, а в другій —6 л. Скільки літрів бензину в двох каністрах?

Завдання. Розв'язати інші задачі з такою самою умовою, але іншими запитаннями:

а) на скільки літрів бензину в першій каністрі більше, ніж у другій?

б) у скільки разів менше бензину в другій каністрі, ніж у першій?

в) скільки літрів бензину потрібно долити, щоб в каністрах бензину стало порівну?

Зміна сюжету задачі. Пропонують розв'язати таку саму задачу, але з іншими величинами. При цьому учні вчаться з'ясовувати умови застосування в реальній дійсності тих чи інших залежностей.

Зміна, деяких зв'язків. Такий прийом привертає увагу дітей до значення окремих слів і виразів у контексті задачі. Вони поступово усвідомлюють, що незначні на перший погляд зміни ведуть до істотних змін у ході розв'язування, роблять висновок про можливість зміни характеру залежностей між величинами.

Задача. У білки 12 горіхів, а в хом 'яка — на 3 горіхи менше. Скільки горіхів у білки і хом 'яка разом ?

Завдання. Замінити в умові вираз "на 3 горіхи менше" іншим — "у 3 рази менше" ("на 3 горіхи більше", "у 3 рази більше") і розв'язати задачу.

Варто практикувати також поступове ускладнення умови задачі. Спочатку учням пропонують кілька змінених задач, в яких збільшується кількість числових даних, включаються додаткові зв'язки. Запитання задачі залишається без змін. Цей прийом дає змогу бачити, як ускладнення числових даних і зв'язків впливає на хід розв'язування задач.

Задача. Турист за день пройшов 10 км і проїхав на автобусі 180 км. Скільки кілометрів пройшов і проїхав турист за день?

Змінені задачі:

/. Турист ішов 2год по 5 км/год та їхав на автобусі 180 км. Скільки кілометрів пройшов і проїхав турист разом ?

2. Турист ішов 2 год по 5 км/год та їхав 3 год автобусом зі швидкістю 60 км/год. Скільки кілометрів пройшов і проїхав турист разом?

3. Пішки турист ішов 2 год, а автобусом їхав на 1 год більше. Він ішов зі швидкістю 5 км/год, а їхав в автобусі зі швидкістю 60 км/год. Скільки кілометрів пройшов і проїхав турист разом ?

Розв'язування задач різними способами. Деякі арифметичні задачі допускають два чи кілька способів розв'язування. Такі задачі є ефективним навчальним матеріалом, на основі якого в учнів пробуджується допитливість, самостійність мислення. Намагання знайти інший шлях розв'язування тієї самої задачі сприяє підвищенню емоційного стану школярів.

Розв'язування задач різними способами веде до розвитку вміння всебічно аналізувати задачну ситуацію. Проте тут важливий ще і сам факт існування266

РозділXI. Навчання учнів розв 'язувати текстові задачі

різних способів розв'язування. Усвідомлення цього є кроком до пошуку кращого способу, що водночас призводить до встановлення нових зв'язків між величинами або використання відомих зв'язків у нових умовах.

Задача. У хлопчика було 8 білих і 7 чорних кролів. 5 чорних кролів він передав шкільній кролефермі. Скільки кролів стало у хлопчика?

Розв'яжіть задачу двома способами.

Перший спосіб Другий спосіб

1) Скільки всього кролів як 1) Скільки чорних кролів у хлопчика? сії і. залишилося?

2) Скільки кролів стало чц,. 2) Скільки кролів стало у хлопчика? у хлопчика?

Зауважимо, що розв'язання, відмінні між собою лише порядком вико­нання дій, не є різними.

Складання виразів за умовою задачі. Як творчий вид роботи над задачею можна розглянути завдання, основна мета яких полягає не у знаходженні числового результату, а у складанні числових виразів. Роль завдань, що сприяють розвитку вмінь учнів записувати деяку конкретну життєву ситуацію математичною мовою, надзвичайно велика. Особливо корисні вони як засіб підготовки дітей до розв'язування задач складанням рівняння. Наведемо зразки таких завдань (див. також розділ XIII):

1. У шкільному хорі 42 учні, а в гуртку малювання — 14. Використовуючи ці числа і знак дії, записати, скільки учнів у хорі і в гуртку малювання разом. Відповідь. 42 + 14.

Змінюючи вимогу до тієї самої умови, можна показати її роль у виборі дії. Так, до розглянутої умови доцільно додати ще такі вимоги: записати у вигляді виразу, на скільки більше учнів у шкільному хорі, ніж у гуртку малювання (42 - 14); записати у вигляді виразу, в скільки разів у гуртку малювання менше учнів, ніж у шкільному хорі (42 : 14).

2. На дереві сиділо 28 галок. 14 галок полетіло, а 7 — прилетіло. Записати у вигляді виразу, скільки галок стало на дереві. Відповідь. 28 — 14 + 7.

3. Лінійка коштує 45 коп., косинець — 40 коп. і блокнот — 90 коп. (Цю умову подати у вигляді таблиці).

Завдання:

а) поясніть, що означають вирази:

45 + 40; 45-40; 45 + 40 + 90; 90:45; 90-45; 90 - (45 + 40).

Відповідь. 45 + 40 — вартість лінійки і косинця; 45 - 40 — на стільки копійок лінійка дорожча, ніж косинець; 45 + 40 + 90 — вартість лінійки, косинця і блокнота; 90 : 45 — у стільки разів лінійка дешевша, ніж блокнот і т. ін.;

б) складіть вирази, за допомогою яких можна визначити, скільки треба заплатити за лінійку і блокнот (45 + 90); на скільки копійок косинець дешевший, ніж блокнот (90 - 40); у скільки разів більше треба заплатити за блокнот, ніж за лінійку (90 : 45);

в) запишіть у вигляді виразів, яку здачу одержить учень з двох гривень, якщо купить лінійку (200 — 45); лінійку і блокнот (200 - (45 + 90)).

> 4. Купили 4 м тканини по 8 грн. за метр. Усього заплатили 32 грн.

Методика викладання математики в початкових класах

Використовуючи умову, поясніть, які величини можна знайти за допомо­гою виразів: 8 • 4; 32 : 4; 32 : 8. Відповідь. 8 • 4 — вартість всієї тканини; 32 : 4 — ціна 1 м тканини; 32 : 8 — кількість куплених метрів тканини.

5. Мотоцикліст їхав 3 год зі швидкістю 60 км/год і проїхав 180 км. Складіть вирази для знаходження швидкості, часу і відстані. Відповідь.

180 : 3 — швидкість; 180 : 60 — час; 60 • 3 — відстань.

6. Турист ішов пішки 3 год зі швидкістю 4 км/год та їхав велосипедом 2 год зі швидкістю 16 км/год. Поясніть, які з поданих виразів мають зміст, а які — ні: 4 • 3; 16 • 2; 16 - 4; 16 + 4; 16 : 2; 2 • 3; 3 + 2; 4 - 3; 4 • 3 + 16 - 2; 16 • 2 - 4 • 3.

Складання задач. Завдання на складання задач ефективні насамперед для розвитку уявлень учнів про структуру задач та узагальнення способу їх розв'язування. Цей вид роботи корисний і для досягнення багатьох інших цілей, зокрема для того, щоб виявити, як діти усвідомлюють способи розв'язування задач певного виду. Якщо учень самостійно складає задачу з певними залежностями між величинами, то він добре розуміє ці залежності і легко сприйматиме відповідний зв'язок у заданій задачі.

У спеціальних дослідженнях з методики математики і досвіду роботи самих учителів обґрунтовано доцільність застосування багатьох прийомів складання задач, кожен з яких має свою функцію. Подамо їх перелік:

• складання задач на зазначену дію;

• складання задач за виразом чи розв'язком;

• складання задач на задану зміну величин чи залежність між величинами. Наприклад, скласти задачу про збільшення маси кроля; скласти задачу на зменшення числа в кілька разів; скласти задачу на знаходження ціни (вартості чи кількості товару; відстані, швидкості чи часу; норми витрат продуктів, урожайності тощо);

• складання задач певного виду. Наприклад, скласти задачу на знаходже­ння невідомого зменшуваного; на знаходження третього доданка за відомою сумою і двома доданками; на різницю двох добутків; на зустрічний рух, в якій потрібно було би знайти час руху;

• складання обернених задач.

Заслуговує на увагу складання і розв'язування задач за числовими даними, що подаються в поєднанні з відповідними малюнками (мал. 135).

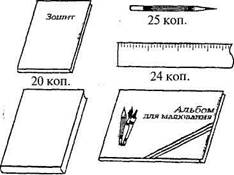
60 коп.

Мал. 135

40 коп. 268

РозділХІ. Навчання учнів розв'язувати т<

Запитання: 1. На скільки копійок олівець дешевший від альбому для малювання? 2. Скільки копійок коштують 2 зошити і книжка разом? 3. У скільки разів книжка та альбом дорожчі за зошит? 4. Скільки копійок заплатять за 3 олівці і 2 лінійки разом?

Як вид творчої роботи практикується також порівняння задач з тією чи іншою метою: звернути увагу учнів на те, що ті самі слова можуть бути як визначальними для вибору дій, так і не визначальними; визначити, яка з двох задач проста, а яка — складена; з'ясувати, яка з даних задач належить до зазначеного виду.

Навчання дітей розв'язувати задачі — це не ізольований процес, він безпосередньо пов'язаний із загальною атмосферою в класному колективі. Слід виховувати інтерес до самостійного розв'язування задач, заохочувати учнів знаходити раціональні прийоми обчислення.