
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Підготовка вчителя до уроку
Дата добавления: 2014-10-22; просмотров: 2134
|
|
З огляду складових частин уроку випливають і вимоги до його підготовки.
Хід уроку має бути відображений у плані-конспекті та достатньо забезпечений дидактичними матеріалами. Кожний учитель має розробити свою методику (технологію) підготовки до уроку. Насамперед треба глибоко продумати тему і цільове спрямування уроку. (Тема зазначена в календарному плані). Після перегляду в підручнику матеріалів для даного уроку і плану-конспекту попереднього уроку (стану його виконання) формулювання теми уточнюється і нерідко доповнюється відповідно до дійсного стану опра-
Методика викладання математики в початкових класах 81
цювання програмного матеріалу. Основна дидактична мета, що здебільшого випливає з теми уроку, має відображати результат дальності учня. Наприклад: "Засвоєння учнями таблиці віднімання числа 5 з переходом через десяток", "Усвідомлення учнями зв'язку між діями додавання і віднімання", "Набування учнями вмінь і навичок письмового додавання трицифрових чисел" та ін.
Намітивши навчальну мету уроку, вчитель продумує, як її найкраще реалізувати на конкретному дидактичному матеріалі з певним складом учнів, іірахувавши їх загальні психологічні та індивідуальні можливості. При цьому потрібно ґрунтовно проаналізувати матеріал підручника: чи достатньо його па урок; чи повністю його використовувати, чи щось опустити; чим і звідки доповнити матеріал підручника; що є в підручнику для опитування, усних обчислень або актуалізації знань; яким методом передбачено опрацювання нового матеріалу в підручнику; що краще учні засвоюють під керівництвом учителя, а що самостійно.
Визначивши методику опрацювання нового матеріалу, час, потрібний для його пояснення і первинного закріплення, треба продумати, скільки можна виділити часу на інші складові частини уроку. З урахуванням часу визначають методику перевірки домашньої роботи, зміст завдань і запитань для опитування учнів та усних обчислень. Ці завдання і запитання, якщо їх нзято не з підручника, варто записати у плані-конспекті. Крім цього, записують відповіді громіздких прикладів, складних задач та формулювання тих правил чи висновків, яких не подано у підручнику.
Добираючи матеріал для закріплення та повторення, продумують також способи диференційованого підходу чи організації виконання завдань за двома нмріантами.
Абстрактний характер математичного матеріалу потребує використання нідиовідних наочних засобів, роздаткового матеріалу, іншого обладнання (ігор, цікавих вправ).
Працюючи над планом уроку, треба враховувати всю систему уроків із 'літальної теми, вимоги до рівня її засвоєння.
Виконанню виховних завдань на уроці сприяють весь навчальний процес шалом, методи навчальної роботи, чітка організація уроку. Проте в системі уроків з теми варто планувати матеріал для виховання в учнів спостережливості, сумлінності та ініціативності, чіткості та охайності в роботі. Зндачі, які розв'язують і складають на уроці, мають бути практичного, Пізнавального характеру, що сприяє встановленню зв'язку з життям.
У ході проведення уроку вчитель додержується плану, але при цьому зважає іііі псі обставини. У разі відхилення від плану важливо зорієнтуватися, як це може вплинути на всю передбачену роботу. Майстерність учителя проявляється в умінні відреагувати на те, як сприймають діти його поясііення, які в них виникають труднощі. Може виникнути потреба в додатковому поясненні, заміні методу роботи, використанні предметної Ілюстрації та ін.
Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 82
§15. Огляд інших різновидів уроків математики
в початкових класах
До інших різновидів уроків математики в початкових класах належать такі уроки: застосування знань, умінь і навичок; узагальнення знань; письмових контрольних робіт.
Ми розглянемо два останніх уроки.
Урок узагальнення знань. У початкових класах у чистому вигляді уроків на узагальнення знань з математики майже не буває. Здебільшого вони вміщують також завдання на формування вмінь і навичок та їх застосування.
Структура уроку узагальнюючого повторення може бути така сама, як і комбінованого уроку. Для цього достатньо в структурі комбінованого уроку опрацювання нового матеріалу замінити на повторення та аналіз основних понять і узагальнення з даної теми. Плануючи уроки на узагальнення, можна об'єднати теми за принципом взаємозв'язку, добирати вправи на комплексне застосування раніше набутих знань, умінь і навичок, широко використовувати стимули, що викликають пізнавальні інтереси учнів до вивченого матеріалу. Розглянемо приклади уроків на узагальнення знань.
Тема "Додавання і віднімання двоцифрових чисел (закріплення та узагальнення)"
(2-й клас).
1. Контроль, корекція та закріплення знань учнів.
1. Перевірка домашньої роботи: а) Скласти і розв'язати задачі (табл. 12).
Повідомити умову і відповідь до кожної задачі.
Таблиця 12
| Було | Відрізали | Залишилося | |
| 1. | ? | 14 м | 36 м |
| 2. | ЗО м | ? | 12 м |
б) Пояснити, як знайшли різницю 70 — 38.
2. Завдання для опитування: а) Обчислити суму 23 + 49 з коментуванням, б) Від найбільшого двоцифрового числа відняти найбільше число четвертого десятка.
3. Усні обчислення. Усно розв'язати задачі: а) Для виготовлення пляшкового скла взяли 10 кг вапна, 30 кг піску, а соди — на 22 кг менше, ніж піску. Скільки кілограмів
суміші отримали?
Учитель повідомляє задачу на основі короткого запису:
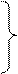 |
Вапна — 10 кг.
Піску — 30 кг. ?
Соди — на 22 кг менше, ніж піску.
б) 3 двох пунктів, відстань між якими 80 м, вийшли одночасно назустріч один одному хлопчик і дівчинка. Хлопчик пройшов 35 м, а дівчинка — ЗО м. Скільки метрів їм залишилося пройти до зустрічі?
На дошці подано графічну ілюстрацію задачі (мал. 27).
Методика викладання математики в початкових класах 83

Мал. 27
II. Узагальнення знань учнів про додавання і віднімання двоцифрових чисел?
1. Випишіть вирази, які обчислено неправильно, й обчисліть їх правилу
23 + 41 = 54 64 - 12 = 62 34 + 51 = 85
52 + 8 = 58 70 - 3 = 67 43 + 9 = 52
58 + 28 = 78 70 - 43 = 37 43 + 30 = 73
2. Бесіда. Ми вивчили усне й письмове додавання і віднімання двоцифрових чисел. Маємо чотири групи випадків додавання і віднімання без переходу через десяток і з переходом через десяток (вирази записано на дошці).
34 + 52 28 + 59 57-34 40-8
54 + 30 38 + 4 79-40 53-8
54 + 3 76 + 4 72-2 63-28
20 + 47 38 + 52 2 + 47 50 - 34
Учні пояснюють обчислення одного-двох виразів з кожного стовпчика, а вчитель узагальнює, що в усіх випадках треба додавати десятки до десятків, одиниці до одиниць і віднімати десятки від десятків, одиниці від одиниць, а також звертає увагу, що в складніших випадках дії можна виконувати письмово.
III. Розвиток математичних знань учнів.
1. Фронтальне опрацювання завдання (на повторення зв'язку компонентів і результату дії віднімання):
а) Зменшуване 26, від'ємник 9. Знайти різницю.
б) Що отримаємо, якщо додамо від'ємник і різницю?
в) Усні обчислення за табл. 13.
Таблиця 13
До чисел другого стовпчика додати числа третього стовпчика. Від чисел п'ятого ОТішпчика відняти числа третього стовпчика. Додати числа першого і четвертого рядків.
2. Завдання додому (за матеріалами підручника).
Підсумок уроку. Розглянули всі випадки додавання і віднімання двоцифрових Чисел в межах 100. Усі випадки Поділяються на такі групи: додавання і віднімання всі переходу через десяток та додавання і віднімання з переходом „через десяток.
Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 84
Додавання і віднімання без переходу через десяток виконували усно, з переходом через десяток — усно і письмово.
Тема "Повторення матеріалу та узагальнення таблиць множення і ділення" (3-й клас).
І. Контроль, корекція та закріплення знань учнів.
Перевірка домашньої роботи. Перша задача — розповісти план розв'язання і повідомити відповідь; друга задача — записати розв'язання на дошці.
Завдання для опитування: 1. Знайти три значення а, при яких правильна нерівність: 6 • а < ЗО. 2. Скласти задачу за виразом: (15 + 12) : 3.
Усні обчислення: 1. Називання результатів таблиць множення. Почергова розповідь таблиць ділення. 2. Знаходження в кожному рядку зайвого числа (за вправою з підручника) (табл. 14).
Таблиця 14
| ЗО | |||||||||
II. Узагальнення знань про таблиці множення і ділення. Ми закінчили вивчати таблиці множення і ділення. Таблиць множення є вісім: множення чисел 2, 3, 4, 5, 6, 7, 8 і 9; стільки ж є таблиць ділення.
Складаючи таблиці множення, ми користувалися означенням дії множення як дії додавання однакових доданків: 7-3 — це 7 + 7 + 7.
При складанні таблиць ділення ми спиралися на зв'язок дій множення і ділення. Так, з приклад
4 • 7 = 28 можна скласти два приклади на ділення: 28 : 4 = 7 і 28 : 7 = 4. Знаючи таблицю множення числа, можна скласти таблицю ділення на це число. Наприклад:
3-2 = 6 6 : 3 = 2
3-3 = 9 9 : 3 = 3
З • 4 = 12 12 : 3 = 4
З • 5 = 15 15 : 3 = 5
Коротко таблиці множення і ділення можна записати в одній зведеній таблиці (таблиці Піфагора).
Потім учні виконують кілька вправ за таблицею Піфагора і за запитаннями вчителя повторюють, як складають таблиці множення і ділення.
III. Розвиток математичних знань учнів.
1. Розв'язування задач (самостійно за варіантами).
І варіант
У швейну майстерню завезли кілька сувоїв тканини по 9 м у кожному. За день використали 45 м, залишилося 27 м тканини. Скільки сувоїв завезли в-1 майстерню?
// варіант
Мати купила 27 кг помідорів. Третю частину маси помідорів вона залишила свіжими, а решту засолила. Скільки кілограмів помідорів мати засолила?
Розв'язання задач записати окремими діями. ,;
2. Обчислення виразів (самостійно за варіантами).
/ варіант. 100-5-5; 5-3 + 4-7; (45 - 27) : 9.
Методика викладання математики в початкових класах 85
11 варіант. 10 + 8-3; 9-4 + 8-6; 8 • (13 - 6).
3. Бесіда про застосування дужок у записах математичних виразів. Виконати вправу: розставити дужки, щоб рівності були правильними.
12 - 4 • 2 = 16; 27 : 3 + 6 = 3; 24 : 6 : 2 = 8.
Якщо буде час, то опрацювати за підручником завдання на побудову квадратів та на розв'язування рівнянь.
4. Підсумок уроку. Розглянули питання, пов'язані зі складанням таблиць множення і ділення. Серед арифметичних дій виділяють табличні й позатабличні випадки. Табличні випадки арифметичних дій учні повинні знати напам'ять.
З наведених зразків уроків видно, що в процесі узагальнення і повторення матеріалу активну участь беруть самі учні.
Уроки письмових контрольних робіт. Контроль і корекція знань, умінь і навичок учнів здійснюються на кожному уроці. А через кожних 10-15 уроків проводяться письмові контрольні роботи. Формуючи їх зміст, учитель враховує результати поточного опитування, він має бути впевненим, що учні в більшості засвоїли відповідний програмовий матеріал. Ступінь складності роботи має бути середнім.
Письмові контрольні роботи бувають комбіновані й одновидові.
Комбінована робота охоплює не більш ніж три види завдань: одну задачу, чотири-десять виразів на виконання арифметичних дій, одну-дві вправи іншого математичного характеру (порівняння виразів, складання й обчислення виразів, перетворення іменованих чисел, побудова геометричних фігур та ін.). Комбінована робота розрахована на один урок.
Наведемо зразки контрольних (самостійних) робіт одного варіанта.
2 клас
1. У першому поїзді 38 вагонів, у другому — на 7 більше, а в третьому — на 12 менше, ніж у другому. Скільки вагонів у третьому поїзді?
2. 28 + 65 68-23 92-20 13-8 + 22 37 + 9 75-4 45+15 89 - (12 - 6)
3 клас
1. За 5 днів на заводі виготовлено 45 телевізорів. Радіоприймачів завод за день випускав на 3 менше, ніж телевізорів. Скільки радіоприймачів ииготовляють на заводі за 7 днів?
2. 8-6 + 72: 8 592-(318-89) 32-49:7 652-374-158 746-328 1кг-370 г
608 - 329 4 м - 70 см
3. Накресліть відрізок завдовжки 85 мм.
4 клас
1. З кожного з 14 га зібрали по 38 ц зерна кукурудзи, а з 1 га — 53 ц. Чпайдіть середню врожайність кукурудзи.
2. 2 555:35 1031-17 5080 : 5 + (3 010 - 817) 6 468:21
6 ц 80 кг: 4 51280:40-5
3. Перше число Ь, друге — у 5 разів більше від нього. Запишіть вираз для (находження суми цих чисел.
Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 86
Розгляньмо організаційні питання проведення і перевірки контрольних робіт. Контрольні роботи проводять на другому або третьому уроці. Протягом тижня учням одного класу пропонують з різних навчальних предметів не більше, як дві письмові роботи, а протягом дня — лише одну.
У початкових класах контрольні чи самостійні роботи з математики практикують в двох варіантах. Добре, коли буде і третій варіант, записаний на окремих аркушах. Його пропонують учням, які навчаються з математики на "З" або взагалі не встигають. Завдання контрольної чи самостійної роботи записують на дошці до початку уроку (на перерві). Щоб вмістити весь текст, використовують переносні дошки.
Поточні контрольні чи самостійні роботи діти виконують в окремих зошитах, а інспекторські роботи — на окремих подвійних аркушах. На першій сторінці аркуша учень зазначає клас і своє прізвище, а завдання він розв'язує на другій (внутрішній) сторінці аркуша.
Перш ніж діти почнуть працювати, вчитель читає вголос текстові завдання; дає вказівки щодо розміщення записів на сторінці аркуша, щодо перевірки правильності розв'язання завдань.
Текстові завдання учні не переписують. Необов'язково також скорочено записувати задачу, оскільки це не входить до змісту контрольної роботи.
Якщо контрольна робота передбачає математичний диктант, то його проводять на початку виконання завдань (спільно для всіх учнів класу). Вчитель диктує вирази, відводячи для запису кожної відповіді 10 с. Діти записують тільки відповіді, а якщо не знають, то проставляють риску.
Час, який відводиться на безпосереднє виконання завдань контрольної (самостійної) роботи, не має перевищувати 20-25 хв у 2 класі, 25-30 хв у З класі і 30—35 хв у 4 класі. Резерв часу уроку використовується для розв'язування задач і вправ.
Під час проведення контрольної роботи необхідно забезпечити повну самостійність виконання учнями завдань. Дітям, які виконають завдання раніше, учитель пропонує додаткові вправи з підручника або на окремих картках. їх розв'язання вони записують у своєму зошиті для класних і домашніх завдань.
Контрольні (самостійні) роботи всі учні здають учителеві одночасно. Перевіряти контрольні роботи бажано в день їх проведення. Оцінюючи їх, учитель керується нормами оцінок, поданими у відповідному методичному листі Міністерства освіти і науки України.
Проаналізувати результати контрольної роботи треба на наступному уроці. Аналіз охоплює загальну характеристику результатів контрольної роботи і аналіз помилок. Спочатку вчитель оцінює роботу класу загалом (чи достатній рівень знань виявили учні класу). Загальна оцінка підтверджується кількістю учнів, які правильно розв'язали задачу та виконали обчислення. Аналіз помилок проводиться у вигляді бесіди. Учитель вказує на помилки у розв'язуванні і пропонує з'ясувати їх причини, розв'язати завдання правильно. Після розбирання помилок у задачах учні розв'язують їх самостійно, обмінявшись варіантами. Як правило, під час аналізу
Методика викладання математики в початкових класах 87
повторюється теоретичний матеріал, який є основою завдань контрольної роботи.
Домашні завдання на цьому уроці подаються з урахуванням результатів контрольної роботи. Зміст домашньої роботи визначається з урахуванням диференційованого підходу.
Більшість контрольних письмових робіт, які проводить вчитель, є тематичною. Директорські та інспекторські роботи за своїм спрямуванням ближчі до підсумкових. Вони охоплюють ту тему, яку учні завершили вивчати на час перевірки, а також найважливіші питання з попередніх тем.
Зауважимо, що інспекторську контрольну роботу в початкових класах повністю організовує (за винятком добору текстів) і проводить сам учитель. Він не тільки записує і ознайомлює учнів із завданнями, а й стежить за їх діяльністю; морально підтримує дітей, які не впевнені в своїх знаннях; пропонує додаткові завдання школярам, які достроково виконали вправи. Важливо добитися спокійного і певною мірою піднесеного настрою під час виконання контрольної роботи.
Відкритий урок
Головна мета відкритих уроків — підвищення майстерності вчителів на основі безпосереднього показу творчих знахідок педагогів і результатів досліджень педагогічної науки. Бажано, щоб у школі була організована постійно діюча система відкритих уроків, що розкриває технологію уроку загалом і певний прийом чи сукупність прийомів навчальної роботи зокрема.
Відкритий урок — це не засіб контролю, а засіб допомоги колегам. Організовувати відкритий урок доцільно в тому разі, коли є впевненість, що пін буде ефективним для присутніх учителів.
За навчально-методичною метою відкриті уроки можна поділити на дві групи.
До першої групи належать уроки, що характеризують технологію уроку загалом. Вони будуть корисні для вчителів-початківців. Тут особливо доцільні уроки в першому класі, уроки на певний вид програмового матеріалу, на певний етап засвоєння знань учнями.
До другої групи належать уроки, що розкривають спосіб організації навчальної діяльності учнів: навчальний прийом, методику застосування того чи іншого методу, використання засобу навчання та ін.
Планувати відкриті уроки можна тільки з урахуванням кадрового складу ичителів певної школи чи району.
Визначимо орієнтовну тематику уроків:
1. Колективно-групові форми організації навчальної діяльності учнів на уроках математики (на різних етапах засвоєння знань). Окремими темами тут можуть бути: навчальні колективно-групові ігри на уроках математики; групові форми виконання учнями самостійної роботи; парне виконання математичних завдань; групова форма контролю знань.
2. Методика використання підручника на різних етапах уроку (в кожному класі окремо).
Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 88
3. Засоби зворотного зв'язку вчителя з учнями і методика їх використання на різних етапах уроку.
4. Прийоми і засоби реалізації диференційованого підходу в організації навчальної діяльності учнів на різних етапах уроку.
5. Застосування методу випереджаючого навчання на уроках математики в роботі зі слабовстигаючими учнями.
6. Застосування нового методу опрацювання програмового матеріалу.
7. Прийоми засвоєння учнями таблиць арифметичних дій.
8. Творча робота над задачею (окремо за класами).
9. Урок закріплення та узагальнення матеріалу з теми (назва теми).
10. Прийоми закріплення та корекції знань учнів у процесі опитування. На відкритих уроках варто розкрити особливості виховної роботи, зв'язок
навчання з життям.
Тему і мету відкритого уроку вчитель має знати заздалегідь. Краще, коли на одну й ту саму тему з однаковою метою готують відкритий урок одночасно два вчителі.
На нашу думку, відкритий урок не слід аналізувати так само, як і урок, відвіданий в порядку контролю. Його не варто оцінювати. Достатньо заслухати самого вчителя про те, що він хотів показати, що вдалося; що вийшло не так, як планувалося; що він може порадити. Далі проводиться бесіда у формі запитань (до вчителя, який проводив урок) і відповідей, обмін думками.
§16. Форми організації навчання учнів математики на уроці
Навчання учнів математики на уроці організовують у формі колективної фронтальної або індивідуальної самостійної роботи, застосовують також і групову форму навчання.
Колективна форма роботи має характер бесіди вчителя й учнів з елементами зв'язного пояснення. В роботі над конкретним математичним матеріалом бесіда використовується на різних етапах його опрацювання.
Особливою формою фронтальної роботи є така, коли учитель сам ставить запитання і сам відповідає на них (за суттю це метод зв'язного викладу, розповіді). Застосування такої форми в початкових класах доцільне, оскільки молодші школярі великою мірою у навчанні наслідують учителя. Коментоване розв'язування завдань учителем призначене найчастіше не для ознайомлення з новим матеріалом, а для подання учням зразків міркування.
У практиці навчання є багато ситуацій, коли необхідно, щоб те саме завдання діти розв'язали одночасно із записом його розв'язання на дошці. Це напівсамостійна робота: один з учнів розв'язує завдання на дошці або коментує розв'язання з місця, а решта розв'язує його в зошитах. Звичайно, вчитель рекомендує дітям працювати самостійно, але учень у будь-який час може побачити запис розв'язання чи почути пояснення ходу розв'язування і звірити його зі своїм.
Напівсамостійна форма роботи може бути застосована: а) у процесі первинного закріплення, тобто під час розв'язування перших після показу
Методика викладання математики в початкових класах 89
вчителем завдань на ознайомлення з новими поняттями чи новими видами задач;
б) під час розв'язування завдань підвищеної складності; в) для порівняння різних способів розв'язування того самого завдання; г) для аналізу помилок, допущених учнями під час самостійного розв'язування завдань; г) у ході підготовки дітей до сприймання нового матеріалу, в тому числі задач нового виду.
Індивідуальна самостійна робота передбачає розв'язування завдання кожним учнем окремо. Вона застосовується на будь-якому з етапів навчання, але найчастіше в процесі розвитку вмінь виконувати завдання того чи іншого виду. Самостійне розв'язування завдань у початкових класах майже завжди для учнів є творчим процесом. Отже, в організації такої роботи слід враховувати вимоги щодо проблемного навчання. Вчитель спрямовує дітей на самостійне розв'язування завдань за допомогою відповідних підготовчих вправ або засобів унаочнення, своєчасно виявляє помилкові міркування учнів у процесі розв'язування завдань і допомагає їм, підтримує при цьому емоційний тонус і впевненість у тому, що кожен з учнів спроможний самостійно розв'язати завдання.
В організації діяльності учнів щодо розв'язування того чи іншого завдання ичитель завжди ставить певну мету і залежно від неї визначає форму роботи. Зрозуміло, що колективна й індивідуальна форми роботи можуть змінюватись навіть у процесі виконання одного завдання. Наприклад, ознайомлення зі змістом задачі було проведено у формі колективної фронтальної роботи, а аналіз задачі, складання плану і її розв'язування вчитель пропонує здійснити самостійно.
Практикуються також групові форми навчання. Здебільшого це парні, ланкові або диференційовано-групові. У початкових класах найчастіше використовують диференційовано-групову форму, що передбачає організацію роботи груп з різними навчальними можливостями. Найчастіше учнів поділяють натри групи: сильнішу, середню і слабку. За диференційовано-груповою формою навчання всі діти здебільшого працюють за завданнями, що мають спільну пізнавальну мету. Для різних за навчальними можливостями груп учнів завдання відрізняються за обсягом, рівнем складності, мірою допомоги.
Під час ознайомлення, наприклад з новою задачею, застосовують два способи диференціації. За першим способом диференційовану роботу організовують у комплексі з фронтальною. Ознайомлення зі змістом нової задачі проводиться фронтально. Наявність різних груп учнів учитель враховує під час первинного закріплення матеріалу. Діти першої і другої груп працюють самостійно за картками або з підручником. З учнями третьої групи вчитель повторно аналізує задачі, розглядає окремі питання, в яких висвітлюється суть задачі, її новизна.
За другим способом учням першої групи надається можливість спробувати самостійно розв'язати задачу нового типу. Вчитель повідомляє мету роботи. Потім роздає їм картки з текстами задач нового виду, а з учнями другої і третьої груп працює над задачами фронтально.
Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 90
Організовуючи самостійну роботу учнів, найчастіше застосовують такі три види диференціації: індивідуалізацію вимог до спільного завдання; надання допомоги в одному з варіантів самостійної роботи (індивідуальна допомога); спрощення одного з двох варіантів самостійної роботи.
Індивідуалізація вимог до спільного завдання. Для всіх учнів учитель записує на дошці або вказує в підручнику одне й те саме завдання, але інструкція його виконання передбачає й деякі прийоми диференціації.
Вимоги до розв'язання завдань. Усім учням пропонується, наприклад, та сама задача, причому одразу подається й додаткове завдання щодо цієї задачі. Такими додатковими завданнями можуть бути: розв'язати задачу іншим способом; скласти вираз за розв'язанням задачі окремими діями; змінити запитання й знайти на нього відповідь, скласти подібну задачу; скласти і розв'язати обернену задачу, записати план розв'язування задачі та ін.
Якщо учням пропонується вправа, наприклад на обчислення виразів, то додатковими завданнями можуть бути: знайти значення виразу іншим способом, всіма можливими способами; записати подібний вираз і обчислити його значення; обчислити значення виразів і записати їх значення в зростаючому (спадному) порядку та ін.
Постановка кількох запитань до умови задачі. Вчитель записує на дошці умову задачі і до неї 2—3 запитання. Кожен учень знаходить відповідь на стільки запитань, на скільки зможе. Зрозуміло, що бажано відповісти на всі запитання.
Додаткове завдання, не пов'язане з основним. Учитель зазначає: "Учням, які першими розв'яжуть завдання, треба спробувати виконати ще й додаткове". Ним може бути: обчислення виразів, розв'язування нової задачі, а найчастіше — завдання з логічним навантаженням. Робота над додатковим завданням припиняється одразу, як тільки вчитель організує учнів на інший вид діяльності. Дітям, які не встигли чи не змогли виконати додаткове завдання, пропонується подумати над ним вдома. Невиконання його не впливає на оцінку роботи учня.
Індивідуальна допомога. Завдання для самостійної роботи пропонується у кількох варіантах. В одному чи двох з них міститься додаткова інформація, розрахована на допомогу в розв'язуванні задач. Реалізується цей вид диференціації найчастіше через індивідуальні картки. Розгляньмо прийоми допомоги.
Конкретизація задачі. До задачі додається малюнок або її короткий запис.
Задача. Довжина першої смужки 10 см, а другої — 8 см. На скільки сантиметрів довша перша смужка від другої? (Мал. 28).
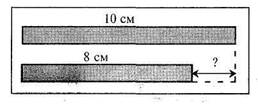
Мал. 28
Методика викладання математики в початкових класах 91
Прочитати задачу, розглянути до неї малюнок і обґрунтувати дію, якою вона розв'язується. Розв'язання записати в зошит.
Повідомлення відповіді до задачі або числових значень виразів. Коли розв'язують задачу на 2-3 дії або знаходять значення виразу, то знання відповіді допомагає аналізувати хід роботи. Знаючи відповідь, учень самостійно виправляє допущену помилку.
Навідні вказівки чи запитання. Вказівки безпосередньо пов'язані з конкретним змістом задач, але взагалі вони бувають на зразок таких: це задача на три дії; для розв'язання задачі буде потрібно виконати дію віднімання, а потім дію множення; подумай, як знайти ціну за вартістю і кількістю товару; будь уважний: блокнотів купили стільки, скільки зошитів; якою дією дізнаємось, у скільки разів одне число більше від іншого?
Початок розв'язування завдання, задачі. У картці подається виконання першої дії або початок аналізу числових даних і запитання для першої дії.
Задача. Якщо шматок дроту розрізати на 4 частини по 16 му кожній, то залишиться ще 6 м. Однак дріт розрізали на частини по 5 м у кожній. На скільки частин розрізали дріт ?
Аналіз. Щоб знайти відповідь, треба знайти довжину всього шматка дроту. Знайдемо довжину за першою частиною умови. Залишилося 6 м. Отже, потрібно ще знайти, скільки метрів дроту розрізали на 4 частини.
Закінчити аналіз задачі, скласти план її розв'язування і розв'язати.
Зразок розв'язання. На картці подано дві задачі одного виду, одна з яких вже розв'язана.
/. Доярка надоїла 96 л молока. 16 л вона віддала телятам, а решту розлила порівну в 4 бідони. Скільки літрів молока доярка налила в один бідон?
1)96— 16 = 80(л);
2)80: 4 = 20(л).
Відповідь. 20 літрів.
2. Виготовили 40 л томатного соку. 13 л соку вилили в сулію, а решту розлили порівну в 9 банок. Скільки літрів соку налили в одну банку?
Перевірити розв'язання першої задачі та розв'язати другу. Подання пояснень чи плану розв'язування задачі.
Задача. На першій ділянці посадили 240 сосен по 20 сосен у кожному ряду, а на другій — 360 акацій по 40 акацій у кожному ряду. На скільки рядів сосен більше, ніж рядів акацій?
Рядів сосен ...
Рядів акацій ...
Більше рядів сосен, ніж рядів акацій на ...
Заповнити пропуски потрібними виразами, виконати обчислення і записати повну відповідь до задачі.
Подання схеми розв'язування чи графічного зображення результату аналізу задачі.
1. На складі було 48 березових і 36 соснових колод. На дошки розпиляли всі березові колоди і четверту частину соснових. Скільки всього колод розпиляли на дошки ?
Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 92
Користуючись схемою, розв'язати задачу, склавши вираз.
2. У магазин привезли 70 кг груш і 3 ящики яблук по 15 кг у кожному. Скільки кілограмів фруктів привезли?
Розв'язати задачу, користуючись вказівками. На мал. 29 показано, що першу дію треба виконувати над даними числами 15 і 3, а другу — над знайденим числом і числом 70.

Мал. 29
Подання інформації, потрібної для розв'язування завдання. Такою інформацією є правила, тлумачення залежностей між величинами та ін.
Наприклад: а) щоб знайти невідоме зменшуване, до різниці слід додати від'ємник; б) щоб за відомою площею прямокутника і його довжиною знайти ширину, треба площу поділити на довжину; в) щоб скласти обернену задачу, потрібно одне з даних (яке саме?) вважати невідомим.
Задача. У минулому році з дослідної ділянки зібрали 14 ц 4 кг ярої пшениці. У цьому році посіяли новий сорт пшениці і з тієї самої ділянки зібрали на 1/6 більше всієї маси пшениці, ніж у минулому. Скільки кілограмів пшениці зібрали з ділянки в цьому році?
Вказівка. Щоб знайти шосту частину числа, треба це число поділити на 6.
Наведені прийоми допомоги, полегшення чи ускладнення завдань за умови неодноразового застосування кожного з них забезпечать практичну основу для реалізації принципу диференційованого підходу в навчанні молодших школярів.
Застосовуючи принцип диференційованого підходу, вчитель має бути тактовним, спиратися на позитивні риси характеру дитини. Не слід оперувати словами "сильні учні", "слабкі учні". Краще відзначити ступінь просування дітей в опануванні вмінь, а також самостійність, оригінальність розв'язку і т. ін.
§17. Перевірка й оцінювання знань, умінь і навичок учнів з математики
Знання, уміння і навички учнів з математики оцінюють за результатами усного опитування, поточних і підсумкових письмових робіт.
Під час перевірки письмових робіт з математики слід розрізняти грубі і негрубі помилки.
До грубих помилок належать:
• обчислювальні помилки в прикладах і задачах;
• помилки у визначенні порядку виконання арифметичних дій:
Методика викладання математики в початкових класах 93
• неправильне розв'язування задачі (пропуск дій (дії)), неправильний добір дій (дії), зайві дії;
• незакінчене розв'язання задачі чи прикладу;
• невиконане завдання (учень не приступив до його виконання). Негрубими помилками є:
• нераціональні прийоми обчислення, якщо ставилась вимога скористатися такими прийомами;
• неправильна побудова чи постановка запитання до дій (дії) під час розв'язування задачі;
• неправильне чи неграмотне з точки зору стилістики або за змістом формулювання відповіді задачі;
• неправильне списування даних (чисел, знаків) задачі з правильним її розв'язанням;
• не доведене до логічного кінця (незакінчене) перетворення. Дві негрубі помилки вважають за одну помилку.
Знання, уміння і навички учнів з математики перевіряються в усній та письмовій формах.
Спільними наказами Міністерства освіти і науки України та Академії педагогічних наук України від 04.09.2002 р. № 428/48 впроваджено 12-бальну шкалу оцінювання навчальних досягнень учнів у системи загальної середньої освіти, а наказом від 12.07.2002 р. затверджено критерії оцінювання навчальних досягнень учнів початкових класів. Ці критерії опубліковано в "Інформаційному збірнику Міністерства освіти і науки України", а також у журналі "Початкова школа" (2002 р., № 8).
Оцінювання навчальних досягнень учнів 1—2 класів здійснюється пербально, 3—4 класів — за 12-бальною шкалою.
За рішенням педагогічної ради загальноосвітнього навчального закладу навчальні досягнення учнів 2 класів можуть оцінюватися в балах.
Впровадження нової системи контролю та критеріїв оцінювання ідійснюється з метою гуманізації та демократизації навчально-виховного процесу, реалізації завдань особистісно орієнтованого навчання. Визначення ріння навчальних досягнень учнів важливе тому, що навчальна діяльність у кінцевому підсумку має дати не тільки суму знань, умінь і навичок, а й сформувати компетентність людини як самоздатність до оптимальних дій.
Оцінювання — це процес встановлення рівня навчальних досягнень учня и оволодінні змістом предмета порівняно з вимогами чинних програм. Об’єктивність і точність оцінок забезпечуються критеріями оцінювання. І якими критеріями є: якість знань, рівень сформованості вмінь, рівень оволодіння досвідом творчої діяльності.
На основі вказаних критеріїв виділяються чотири інтегрованих рівні досягнень учнів початкових класів:
I рівень — початковий — 1 — 3 бали;
II рівень — середній — 4 - 6 балів;
I11 рівень — достатній — 7 — 9 балів;
IV рівень — високий — 10 — 12 балів.
Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 94
Подамо рекомендації для оцінювання усних відповідей.
Високий рівень — учень правильно відповідає на всі запитання, самостійно застосовує на практиці окремі теоретичні положення; без помилок і доволі швидко обчислює, свідомо використовуючи властивості арифметичних дій; самостійно розв'язує задачі й пояснює хід розв'язування; безпомилково називає відомі геометричні фігури, вміє виконати практичне завдання — виміряти чи накреслити; виконує прості вправи, пов'язані з буквеною символікою (читання буквених виразів, знаходження їх значень за даними числовими значеннями букв, розв'язування рівнянь відповідно до програми).
Достатній рівень — коли відповідь загалом задовольняє попередні вимоги, але учень допускає окремі неточності у поясненні математичних фактів, прийомів обчислень; не завжди використовує в обчисленнях раціональні прийоми, часом припускається негрубих помилок; працюючи над задачею, не зовсім точно пояснює хід розв'язування чи результати дій; допускає огріхи, виконуючи вимірювання і креслення. Усі ці недоліки школярі легко виправляють за вказівкою вчителя.
Середній рівень — якщо учень правильно розв'язує більшість запропонованих прикладів, але не вміє пояснити прийом обчислення; допускає в обчисленнях помилки, які виправляє за допомогою вчителя; хоч і помиляється у розв'язуванні задачі, поясненні, проте за допомогою вчителя виконує завдання.
Початковий рівень — учень не засвоїв більшої частини програмового матеріалу, не може впоратися з розв'язуванням задачі та обчисленнями навіть за допомогою класовода.
Для зразка за журналом "Початкова школа" подамо норми оцінювання письмових робіт з математики.
| Рівень навчальних досягнень | Бали | Норми оцінювання навчальних досягнень учнів |
| Початковий | Робота виконана, але допущено 9 і більше помилок. | |
| Робота виконана, але допущено 8 грубих помилок або правильно виконано 1/3 запропонованих завдань. | ||
| Робота виконана, але допущено 7 грубих помилок. | ||
| Середній | Робота виконана, але допущено 6 грубих помилок. | |
| Робота загалом виконана, але допущено 5 грубих помилок або правильно виконано 1/2 запропонованих завдань. | ||
| Робота виконана в повному обсязі, але допущено 4 грубі помилки. | ||
| Достатній | Робота виконана в повному обсязі, але допущено 3 грубі помилки. |
Методика викладання математики в початкових класах 95
| <== предыдущая лекция | | | следующая лекция ==> |
| Підсумок уроку | | | Підсумкове оцінювання знань, умінь і навичок |