Інструменти, прилади й моделі, технічні засоби навчання

Дата добавления: 2014-10-22; просмотров: 2914

В монографии применен системный под­ход к рассмотрению психического разви­тия человека как динамического, целост­ного, хотя и внутренне противоречивого процесса. Дана характеристика психи­ческого развития индивида на протяжении всего жизненного цикла, включая раннее детство, дошкольный и школьный периоды, а также периоды взрослости и старения. Показана диагностическая значимость ос­новных закономерностей психического развития человека, позволяющая созна­тельно управлять этим процессом.

Предназначена для широкого круга психологов, медиков, педагогов.

Заказы, направлять по адресу:

191186, Ленинград, Невский пр., д. 28. Магазин № 1 «Дом книги». Отдел «Книга — почтой».

Інструменти, прилади й моделі, технічні засоби навчання

Вивчення чисел і величин ґрунтується на практичній діяльності учнів, пов'язаній з оволодінням уміннями і навичками вимірювання довжини відрізка, площі фігури, маси тіла, місткості посудини, часу. Вимірювати ці величини можна за допомогою інструментів. Вони поділяються на демонстраційні та індивідуальні. Деколи замість самих інструментів використовують їх моделі (моделі циферблата годинника, терезів, малки тощо).

Класна рахівниця (мал. 8) служить необхідним наочним посібником для вивчення нумерації чисел в межах 1 000 000. Нею користуються з І класу, поступово збільшуючи кількість дротинок. На рахівниці під час вивчення чисел у межах 10 можна ознайомити учнів з тим, як отримати наступне і попереднє числа, як порівнювати числа (кількість кісточок на двох дротинках); демонструвати склад числа; проводити лічбу, додавати і віднімати числа; розкривати поняття "збільшити (зменшити) на кілька одиниць"; складати таблиці додавання і віднімання.

Мал. 8

Методика викладання математики в початкових класах 39

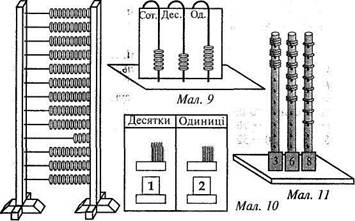
Для ознайомлення з письмовою нумерацією чисел можна використати рахівниці з вертикальними дротинками (мал. 9), предметний абак (мал. 10).

Для вивчення нумерації чисел та окремих випадків додавання і віднімання застосовуються різноманітні демонстраційні абаки (мал. 11, 12). Індивідуальні абаки (мал. 13) побудовані так само, як демонстраційні (мал. 12).

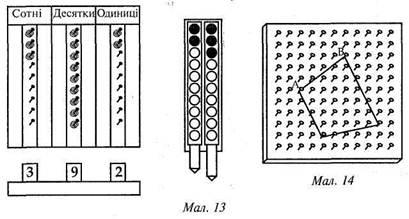
Велике значення в навчанні математики мають моделі і набори геометричних фігур. Значну частину задач геометричного змісту можна відтворити на посібнику, який являє собою дошку (фанеру) із вбитими в неї гвіздками на відстані 5 см один від одного (гвіздки над поверхнею дошки виступають на 1—2 см) (мал. 14).

Для роботи з посібником використовують кольорові гумки. За допомогою такого посібника можна швидко відтворювати, змінювати геометричні фігури, розв'язувати як прості, так і складені задачі геометричного змісту.

До технічних засобів навчання математики належать кінопроектори, діапроектори, епідіаскопи, кодоскопи. Вони допомагають у багатьох випадках замінити записи на класній дошці під час пояснення вчителем нового матеріалу.

Найпоширенішими серед різних екранних засобів навчання є діафільми. Вони розраховані на вивчення учнями нового матеріалу і служать ілюстрацією до пояснення. Окремі фрагменти можуть бути використані на етапах закріплення, повторення й узагальнення знань та з метою контролю знань, умінь і навичок.

Діапозитиви — це своєрідні окремі кадри діафільму. Проте вони можуть бути виготовлені самим учителем. На плівку наносяться потрібні записи чи малюнки. Діапозитиви демонструють за допомогою епідіаскопа.

Кодоскоп поєднує в собі можливості класної дошки і діапроектора. Матеріал для кодоскопа, як і для епідіаскопа (епікадри і епістрічки), за змістом і художнім оформленням може добирати і виготовляти сам учитель.

Розділ III. Засоби навчання математики в початкових клас 40

У 3—4 класах учням варто показати застосування комп'ютера для розв'язування задач.

Під час підготовки до уроку з використанням технічних засобів навчання слід визначити місце і час демонстрації екранного посібника; зазначити місце зупинок для проведення бесіди, самостійної або інших видів роботи, а також місця, коли треба дати додаткові пояснення під час демонстрації екранного посібника; продумати зміст цих пояснень.

§11. Засоби зворотного зв'язку

Виконуючи завдання з усних обчислень, учні піднімають руку і з дозволу вчителя усно повідомляють відповідь. Нерідко вчителі пропонують дітям показати відповіді за допомогою розрізних цифр. Це допомагає залучати до роботи всіх учнів, а вчитель бачить, як діти впорались із завданням. Зас­тосування розрізних цифр зручне для випадку дій у межах 10. За межами десятка повідомлення відповідей за допомогою розрізних цифр дещо ускладнюється. Тому в практиці розроблені й інші засоби зворотного зв'язку. Розглянемо деякі з них.

Віяло (мал. 15). Розрізні цифри скріплені у вигляді віяла.

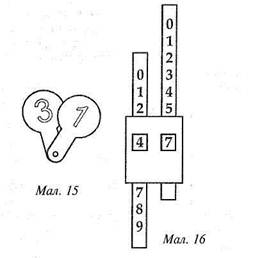
Числовий абак (мал. 16). Цей пристрій складається з двох стрічок, на кожній з яких записані одноцифрові числа. Вони можуть рухатись у картонній рамці. У рамці зроблені віконця для чисел. Для повідомлення відповіді, наприклад 47, учень має розмістити стрічки так, щоб це число з'явилося в рамочці.

Методика викладання математики в початкових класах 41

Таблиця чисел першої сотні. Числа першої сотні записують на подвійному аркуші з учнівського зошита: у першому рядку числа 1—10, у другому — 11—20 і т. д. Висота цифри 17 мм. На зворотному боці всі числа можна записати висотою в одну клітинку. Малі цифри записують навпроти відповідних великих.

Повідомляючи відповідь, учень піднімає аркуш і паличкою (олівцем, ручкою) показує потрібне число.

Таблиця 8

Кодування відповіді. Для швидкого оцінювання правильності відповіді достатньо, якщо учень повідомить не саму відповідь, а стовпчик, в якому є шукане число. У такому разі учневі достатньо мати тільки розрізні цифри.

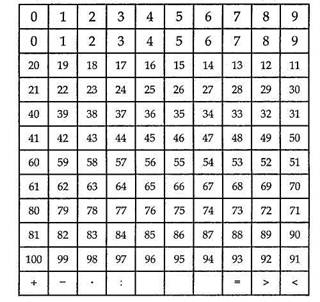
Для кодування відповіді можна також використати таблицю чисел першої сотні (табл. 8). Ця таблиця доповнена верхнім рядком (цифровим кодом) і нижнім рядком (для знаків арифметичних дій і знаків порівняння). Числа в таблиці записані "змійкою".

Нехай учні 2-го класу виконали такі завдання:

57+14 = 71(9) 51-17 = 34(6)

З • 7 = 21 (0) 36 : 4 = 9 (8)

Учні записують відповідь, а поряд у дужках кодовані відповіді. На прохання вчителя вони показують кодовані відповіді цифрами. Цифра 9 означає, що шукана відповідь (71) знаходиться у дев'ятому стовпчику.

РОЗДІЛ IV

СКЛАДОВІ ЧАСТИНИ УРОКУ МАТЕМАТИКИ. МЕТОДИ ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ

Урок математики — основна форма організації навчальної діяльності молодших школярів. В уроці реалізується освітня, виховна та розвивальна мета навчання математики.

Освітня мета полягає в засвоєнні учнями математичних понять та у формуванні в них специфічних для математики вмінь і навичок. У початковій школі учні засвоюють елементарні математичні поняття про число і дії, задачу, величини і вимірювання, про геометричні фігури. Крім математичних, формуються також загальнотрудові знання, вміння і навички. До них належать: організаційні (опанування способів організації свого навчання, зокрема вміння планувати роботу і користуватися підручником); загальнопізнавальні (вміння спостерігати, міркувати, запам'ятовувати і відтворювати матеріал); загальномовленнєві (основні елементи культури слухання і мовлення); контрольно-оцінні (засвоєння способів перевірки та самоперевірки, оцінювання здобутих результатів).

Виховна мета передбачає формування в учнів уявлення про світ загалом, місце людини в ньому і способи його пізнання; вказує загальні орієнтири засвоєння нагромадженого людством соціального досвіду, магістральні шляхи перетворення дійсності.

У процесі навчання математики виховуються вольові якості людини: наполегливість у доведенні справи до кінця, охайність, самостійність, кмітливість, ініціативність.

Розвивальна мета полягає в тому, щоб добитися розвитку в учнів пізнавальних здібностей (сприймання, пам'яті, уяви, мови), мотивів і потреб навчання, творчих можливостей, емоційної сфери.

У педагогіці визначено такі вимоги до уроку: його чітка цілеспрямованість, теоретична й практична повноцінність змісту; правильне застосування та поєднання різних форм організації пізнавальної діяльності учнів (класної, групової, індивідуальної); виразне формулювання основних висновків; достатнє закріплення і повторення нового матеріалу; оперативне з'ясування лупеня оволодіння знаннями.

Для ефективного уроку математики характерні такі особливості: широке застосування фронтальних форм перевірки знань, надання опитуванню навчального спрямування, поєднання функцій контролю і закріплення;

Методика викладання математики в початкових класах 43

проведення на уроці самостійної роботи, спрямованої на оволодіння новим матеріалом; посилення ролі первинного закріплення, збільшення обсягу практичних робіт і тренувальних вправ.

На кожному уроці передбачені встановлення свідомої трудової дисципліни, живе спілкування з учнями, емоційне мотивування навчальної діяльності школярів.

За основною дидактичною метою виділяють такі типи уроків: 1)урок засвоєння нових знань; 2) урок засвоєння навичок і вмінь; 3)урок застосування знань, навичок і вмінь; 4) урок узагальнення і систематизації знань; 5) урок перевірки, оцінювання і корекції знань, умінь і навичок; 6) комбінований урок.

У початкових класах немає уроків, повністю присвячених вивченню нового матеріалу. Новий матеріал невеликими частинами розглядають майже на кожному уроці. Тому найпоширенішими в початкових класах є комбіновані уроки.

Комбінований урок містить такі компоненти: 1) перевірка домашнього завдання; 2) опитування учнів; 3) усні обчислення; 4) підготовка до вивчення нового матеріалу і повідомлення теми заняття; 5) опрацювання нового матеріалу; 6) первинне закріплення; 7) закріплення й повторення; 8) до­машнє завдання та підбиття підсумків уроку.

У структурі комбінованого уроку його компоненти можна об'єднати в такі три частини:

1. Контроль, корекція та закріплення знань учнів (перевірка домашнього завдання, опитування учнів та усні обчислення).

2. Опрацювання нового матеріалу (підготовка до вивчення нового матеріалу, його вивчення та первинне закріплення).

3. Закріплення та узагальнення знань учнів (закріплення і повторення матеріалу, завдання додому, підбиття підсумків уроку). Цю частину часто називають "розвиток математичних знань учнів".

Розгляд окремих частин і компонентів комбінованого уроку подаємо в наступних трьох параграфах. У решті параграфів цього розділу розглянемо інші різновиди уроків, форми навчальної діяльності учнів і нормативи оцінювання їхніх знань.

§12. Контроль, корекція та закріплення знань учнів

Компоненти першої частини уроку — перевірка домашньої роботи, опитування учнів і усні обчислення — взаємопов'язані. Ці компоненти уроку використовують як для контролю, так і для закріплення знань. Нерідко їх важко розрізнити, визначити момент переходу від одного до іншого. Проте кожний зі згаданих видів робіт має свою специфіку, тому методику проведення кожного з них розглядатимемо окремо.