
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Стаття 42. Підозрюваний
Дата добавления: 2015-08-27; просмотров: 691
|
|
Для получения данных в целях ответа на первый вопрос требуется подсчитать общее количество решенных задач, предшествующее устойчивому осуществлению испытуемыми оптимального поиска в случае предъявления первого и второго набора гипотез.
Как уже указывалось, оптимальным способом поиска для I набора гипотез будет опробование любой карточки с вероятностью получения положительного ответа 1/2. Для II набора гипотез необходимо опробовать уже две карточки: первую – с вероятностью получения ответа «да» – 1/2, и вторую, вероятность получения ответа «да» которой будет 1/2 после осуществления первого выбора.
В табл. 1 показано распределение вероятностей получения положительного ответа для I набора гипотез при расположении карточек первой части опыта.
Для получения данных по второму вопросу требуется проследить, каким образом испытуемый осуществляет поиск в каждой конкретной задаче, для чего требуется подсчитать количество информации, получаемой им при осуществлении каждого выбора.
При предъявлении I набора гипотез это делается просто, так как из приведенных выше формул ясно, какое количество информации получает испытуемый в каждом выборе. Экспериментатор должен фиксировать, на каком этапе испытуемым получена требуемая информация 1 дв. ед. и как долго продолжается после этого последующий поиск. При каждом выборе в этом случае испытуемый будет получать нулевую информацию.
При предъявлении II набора гипотез дело несколько усложняется, так как после первых выборов по–разному будет изменяться статистическая характеристика обследуемого поля, и экспериментатор должен сам научиться ее определять. Покажем на примере, как это делается. Предположим, что испытуемый первым назвал объект «3 синих круга на желтом фоне». Из табл. 2 видно, что вероятность получения положительного ответа при выборе этой карточки равна 0, и полученная информация, следовательно, тоже равна 0; статистическая характеристика поля остается неизменной.
Допустим теперь, что испытуемый назвал карточку «3 черных квадрата на белом фоне». Вероятность получения положительного ответа в этом случае равна 1 и, следовательно, полученная информация также равна 0 при неизменной статистической характеристике поля. Возьмем, наконец, случай первого выбора испытуемым карточки, характеризующейся некоторой средней вероятностью получения положительного ответа о принадлежности ее к задуманной группе, например карточки «1 черный круг на белом фоне». Из табл. 2 видно, что вероятность ее равна 0,5. Следовательно, при ее выборе испытуемый получает 1 дв. ед. информации. Экспериментатор должен рассуждать следующим образом: если ответ положительный, следовательно, искомыми могут оставаться или группа «все черные фигуры», или группа «черные фигуры на белом фоне», а группы «3 квадрата» и «3 черные фигуры» быть не могут. Если же ответ отрицательный, напротив, остаются возможными последние две гипотезы. Исходя из этих соображений составляется новая статистическая характеристика поля: при положительном ответе (табл. 3) и отрицательном ответе (табл. 4).
1. Матрица вероятностей получения ответа «да» при проверке каждого объекта для I набора гипотез

2. Матрица вероятностей получение ответа «да» при проверке каждого объекта для II набора гипотез
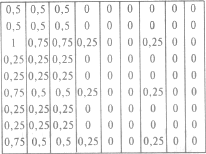
3. Измерение значений вероятности получения ответа «да» при проверке каждого объекта перед вторым выбором после получения положительного ответа на первый выбор (II набор гипотез)
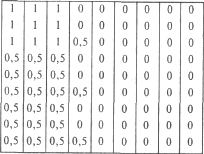
4. Измерение значений вероятности получения ответа «да» при проверке каждого объекта перед вторым выбором после получения отрицательного ответа на первый выбор (II набор гипотез)

Экспериментатор может не чертить в каждом случае новую статистическую характеристику поля, а вычислять устно получаемую информацию при каждом выборе. Данные о количестве информации, получаемой испытуемым при каждом выборе, заносятся в табл. 19. После заполнения таблицы экспериментатором строится график (для первого выбора по I набору гипотез и для первого и второго выбора в отдельности по II набору гипотез), на котором по горизонтальной оси откладывается номер решаемой задачи, а на вертикальной оси – количество информации, полученной испытуемым (рис. 13).
 № задания
№ задания
Рис. 13.График изменения количества информации, получаемой испытуемым.
| <== предыдущая лекция | | | следующая лекция ==> |
| Оперуповноважений ГУБОЗ | | | ПОВІДОМЛЕННЯ |