Перша світова війна закінчилася.

Дата добавления: 2015-08-31; просмотров: 703

Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции из­держек производства, в макроэкономических расчетах и целого ряда других вопросов эконометрики. В настоящее время множе­ственная регрессия - один из наиболее распространенных мето­дов в эконометрике. Основная цель множественной регрессии - построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.

Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Она включает в себя два круга вопросов: отбор фак­торов и выбор вида уравнения регрессии. Их решение при пост­роении модели множественной регрессии имеет некоторую спе­цифику, которая рассматривается ниже.

Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требова­ниям.

1. Они должны быть количественно измеримы. Если необхо­димо включить в модель качественный фактор, не имеющий ко­личественного измерения, то ему нужно придать количествен­ную определенность (например, в модели урожайности качество почвы задается в виде баллов; в модели стоимости объектов не­движимости учитывается место нахождения недвижимости: рай­оны могут быть проранжированы).

2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.

Включение в модель факторов с высокой интеркорреляцией, когда R_yx1 < R_x1x2 для зависимости у = а + b₁∙ х₁ + b₂ ∙ х₂ + может привести к нежелательным последствиям — система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.

Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми. Так, в уравнении у = а + b₁ · х₁ +b₂ · х₂ + предполагается, что факторы х₁ и х₂ независимы друг от друга, т. е. r_x1x2 = 0. Тогда можно говорить, что параметр b₁ измеряет си­лу влияния фактора х₁ на результат у при неизменном значении фактора х₂. Если же r_x1x2 = 1, то с изменением фактора x_l фактор х₂ не может оставаться неизменным. Отсюда b₁ и b₂ нельзя интер­претировать как показатели раздельного влияния х₁ и х₂ и на у.

Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором ρ факторов, то для нее рассчитывается показа­тель детерминации R², который фиксирует долю объясненной ва­риации результативного признака за счет рассматриваемых в ре­грессии p факторов. Влияние других не учтенных в модели фак­торов оценивается как 1 — R² с соответствующей остаточной дис­персией S².

При дополнительном включении в регрессию p+ 1 фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться:

Если же этого не происходит и данные показатели практиче­ски мало отличаются друг от друга, то включаемый в анализ фак­тор x_p+1 не улучшает модель и практически является лишним фактором. Так, если для регрессии, включающей пять факторов, коэффициент детерминации составил 0,857 и включение шесто­го фактора дало коэффициент детерминации 0,858, то вряд ли це­лесообразно дополнительно включать в модель этот фактор.

Насыщение модели лишними факторами не только не снижа­ет величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по t-критерию Стьюдента.

Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости. Отбор факторов производится на основе качест­венного теоретико-экономического анализа. Однако теоретичес­кий анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков и це­лесообразности включения фактора в модель. Поэтому отбор факторов обычно осуществляется в две стадии: на первой подби­раются факторы исходя из сущности проблемы; на второй — на основе матрицы показателей корреляции определяют t-стати­стики для параметров регрессии.

Коэффициенты интеркорреляции (т. е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменных явно коллинеарны, т. е. находятся между собой в линейной зависимости, если r_хixj. > 0,7.

Поскольку одним из условий построения уравнения множе­ственной регрессии является независимость действия факторов, т. е. R_хixj. = 0, коллинеарность факторов нарушает это условие. Ес­ли факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочте­ние при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множест­венной регрессии как метода исследования комплексного воз­действия факторов в условиях их независимости друг от друга.

Пусть, например, при изучении зависимости у =f(x, z, ν) мат­рица парных коэффициентов корреляции оказалась следующей:

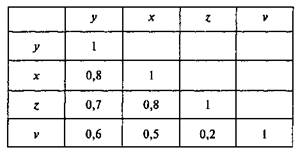
Очевидно, что факторы xи z дублируют друг друга. В анализ целесообразно включить фактор z, а не x, так как корреляция z с результатом у слабее, чем корреляция фактора x с у (r_yz < r_yx), но зато слабее межфакторная корреляция r_zv < r_xv. Поэтому в данном случае в уравнение множественной регрессии включаются факто­ры z, ν.

По величине парных коэффициентов корреляции обнаружи­вается лишь явная коллинеарность факторов. Наибольшие труд­ности в использовании аппарата множественной регрессии воз­никают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимос­тью, т. е. имеет место совокупное воздействие факторов друг на друга.

Наличие мультиколлинеарности между признаками приводит к:

· Искажению величины параметров модели, которые имеют тенденцию к завышению;

· Изменению смысла экономической интерпретации коэффициентов регрессии;

· Слабые обусловленности системы нормальных равнений;

· Осложнению процесса определения наиболее существенных факторных признаков.

В решении проблемы мультиколлинеарности моно выделить несколько этапов:

· Установление наличия мультиколлинеарности;

· Определение причин возникновения мультиколлинеарности;

· Разработка мер по её устранению.

Причинами возникновения мультиколлинеарности между призанками являются:

· Изучаемые факторные признаки, характеризующие одну и ту же сторону явления или процесса. Например, показатели объема производимой продукции и среднегодовой стоимости основных фондов одновременно включать в модель не рекомендуется, так как они оба характеризуют размер предприятия;

· Использование в качестве факторных признаков показателей, суммарное значение которых представляет собой постоянную величину;

· Факторные признаки, являющиеся составными элементами друг друга;

· Факторные признаки, по экономическому смыслу дублирующие друг друга.

Одним из индикаторов определения наличия мультиколлинеарности между признаками является превышение парным коэффициентом корреляции величины 0,8 (r_{xi xj}) и др.

Устранение мультиколлинеарности может реализовываться через исключение из корреляционной модели одного или нескольких линейно-связанных факторных признаков или преобразования исходных факторных признаков в новые, укрупненные факторы.

Вопрос о том, какой из факторов следует отбросить, решается на основании качественного и логического анализов изучаемого явления.

Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования методов рег­рессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии соответственно к разным методикам. В зависимости от того, какая методика построения уравнения ре­грессии принята, меняется алгоритм ее решения на ЭВМ.

Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:

• метод исключения;

• метод включения;

• шаговый регрессионный анализ.

Каждый из этих методов по-своему решает проблему отбора факторов, давая в целом близкие результаты — отсев факторов из полного его набора (метод исключения), дополнительное введе­ние фактора (метод включения), исключение ранее введенного фактора (шаговый регрессионный анализ).

На первый взгляд может показаться, что матрица парных ко­эффициентов корреляции играет главную роль в отборе факто­ров. Вместе с тем вследствие взаимодействия факторов парные коэффициенты корреляции не могут в полной мере решать во­прос о целесообразности включения в модель того или иного фактора. Эту роль выполняют показатели частной корреляции, оценивающие в чистом виде тесноту связи фактора с результа­том. Матрица частных коэффициентов корреляции наиболее широко используется в процедуре отсева факторов. При отборе факторов рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6—7 раз меньше объема совокупности, по которой строится регрессия. Если это соотно­шение нарушено, то число степеней свободы остаточной вариа­ции очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а F-критерий меньше табличного значения.