
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Було взято курс на утворення єдиної соціалістичної держави.
Дата добавления: 2015-08-31; просмотров: 663
|
|
У функции ЛИНЕЙН() следующая синтаксическая запись
ЛИНЕЙН (известные_значения_y; известные_значения_x;ИСТИНА;ИСТИНА)
Если третий аргумент равен ЛОЖЬ, в уравнении отсутствует константа. Изменение четвёртого аргумента на ЛОЖЬ приведет к пропуску расчёта большого числа параметров регрессии, и функция ЛИНЕЙН() вернёт только уравнение множественной регрессии.
Для применения функции ЛИНЕЙН() к m независимым переменным на рабочем листе А удалены выделите диапазон F5:H9.
Введите формулу =ЛИНЕЙН(B4:B22; C4:D22; ИСТИНА; ИСТИНА). Затем нажмите <Ctrl>+<Shift>+<Enter>. Результат представлен на рис. 7.
В строке 5 находится описание уравнения прогнозирования (коэффициенты приводятся справа налево, начиная с константы):
Прогнозируемые месячные расходы = 35475.3+
+  (Произведенные В)+
(Произведенные В)+  (Произведенные изделия С).
(Произведенные изделия С).
В строке 6 содержатся стандартные ошибки приближенного расчёта всех коэффициентов, но они не слишком важны. В ячейке F7 приведено значение R2=0.61, а в ячейке G7 – стандартная ошибка регрессии, равная 1274. В строках 8 и 9 содержится информация (F-статистика, степени свободы, регрессионная сумма квадратов и остаточная сумма квадратов), которая тоже не имеет большого значения.
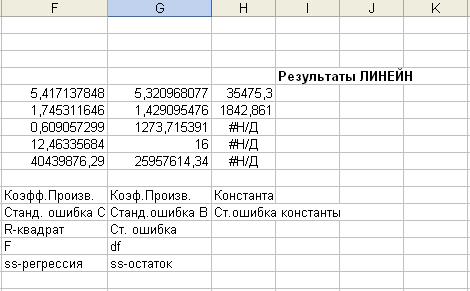
Рис. 7. Применение функции ЛИНЕЙН() для вычисления параметров множественной регрессии
Оценка параметров множественной регрессии с использованием метода обратной матрицы
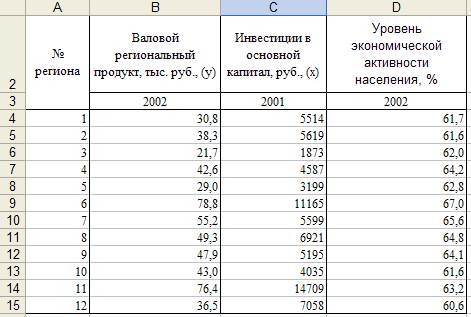
Условие. Имеются данные по 12 регионам одного из федеральных округов России о валовом региональном продукте (ВРП), инвестициях в основной капитал в расчете на душу населения и уровне экономической активности населения, представленные в виде электронной таблицы в MS EXCEL (рис. 1).
1. Исходные данные
Требуется, используя средства MS EXCEL:
1. представить исходные данные в матричной форме и найти оценки параметров уравнения множественной регрессии с использованием метода обратной матрицы;
2. рассчитать и оценить показатели тесноты связи между признаками;
3. дать оценку значимости уравнения в целом и его параметрам, провести интерпретацию коэффициентов чистой регрессии;
4. проверить правильность проведенных расчетов, построив множественную модель с использованием встроенного инструмента «Регрессия»;
5. рассчитать и оценить прогнозное значение валового внутреннего продукта для округа.
.
Методические указания.
1. Постановка проблемы. Уровень ВРП в расчете на душу населения является основным показателем эффективности экономики региона, уровня жизни населения. Аналогом данного показателя на уровне страны является валовой внутренний продукт (ВВП), увеличение которого является общенациональной задачей.
2. Информационной базой являются данные по 12 регионам РФ из 89. Исследуемая совокупность регионов является выборкой. Число наблюдений в расчете на фактор удовлетворяет минимальным требованиям (напомним, что, по мнению разных ученых, на каждый фактор, включенный в модель должно приходиться от 6-7 до 10 наблюдений как минимум).
3. Спецификация модели (отбор факторов и установление формы связи между ними).
Известно, что уровень ВРП на душу населения – основной показатель уровня жизни, зависит от множества факторов. По имеющимся эмпирическим данным построим множественную модель связи уровня ВРП (у) с инвестициями в основной капитал (х1) в расчете на душу населения и уровнем экономической активности (х2). Предположим, что связь линейная:
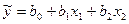 .
.
4.1. Представим исходные данные в матричной форме и дадим оценку параметров уравнения регрессии.
Метод обратной матрицы в приложении к множественному регрессионному анализу позволяет найти вектор оценок коэффициентов чистой регрессии следующим образом:
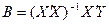 .
.
Умножение на транспонированную матрицу производится для того, чтобы получить квадратную матрицу 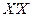 и матрицу
и матрицу 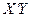 размера (р+1)×1 (р равно числу факторов, р+1 – число параметров уравнения, включая свободный член), одинаковую по размерам с матрицей В (метод применим только в этом случае).
размера (р+1)×1 (р равно числу факторов, р+1 – число параметров уравнения, включая свободный член), одинаковую по размерам с матрицей В (метод применим только в этом случае).
Представим исходные данные в матричной форме:
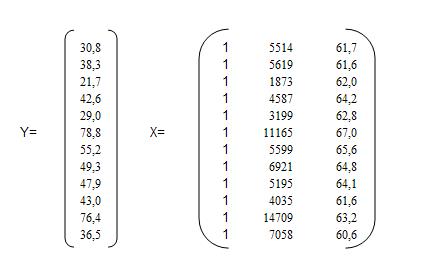
Единичный столбец в матрице Х – это фиктивная переменная, все значения которой равны единице. Он необходим для оценки значения свободного члена.
Последовательно найдем транспонированную матрицу 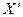 , произведение матриц
, произведение матриц 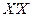 и
и 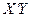 , обратную матрицу
, обратную матрицу 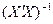 и вектор В как произведение матриц
и вектор В как произведение матриц 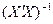 и
и 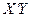 . Для умножения, нахождения обратной матрицы будем использовать встроенные математические функции: «МУМНОЖ(массив1 (первая матрица); массив 2 (вторая матрица))» и «МОБР(массив (матрица))». Вводятся они как формулы массива, т.е. сначала выделяется выходной диапазон, затем вводится формула, делаются соответствующие ссылки на исходные диапазоны, а для завершения нажимается комбинация клавиш – Ctrl+Shift+Enter.
. Для умножения, нахождения обратной матрицы будем использовать встроенные математические функции: «МУМНОЖ(массив1 (первая матрица); массив 2 (вторая матрица))» и «МОБР(массив (матрица))». Вводятся они как формулы массива, т.е. сначала выделяется выходной диапазон, затем вводится формула, делаются соответствующие ссылки на исходные диапазоны, а для завершения нажимается комбинация клавиш – Ctrl+Shift+Enter.
Напомним, что обратную можно найти только к квадратной матрице, т.е. при нахождении обратной матрицы выходной диапазон будет такого размера, что и исходная матрица. При умножении матриц нужно помнить, что число столбцов первой матрицы должно быть равно числу строк второй матрицы, т.е. можно умножить только матрицу размером m×k на матрицу размером k×n, при этом будет получена матрица – m×n.
Транспонирование в EXCEL можно произвести путем копирования исходной матрицы, а затем с помощью пункта «Специальная вставка» контекстного меню. При этом, если исходная матрица получена расчетным путем с использованием ссылок на ячейки, то необходимо установить маркер на «Значения»:
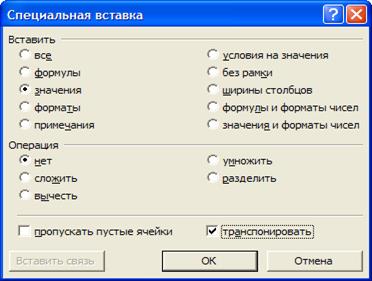
А также можно использовать встроенную формулу массива «Трансп(массив)».
Итак, в ходе решения задачи были получены матрицы:

Выборочная модель множественной линейной регрессии может быть записана в виде:


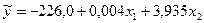 .
.
4.2 Определим показатели тесноты связи.
Коэффициент множественной детерминации:

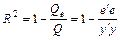 ,
,
где 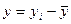 ;
;
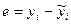 ,
, 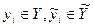 .
.
В свою очередь 
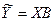 .
.
Множественный коэффициент корреляции (R) и скорректированный коэффициент детерминации ( 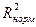 ):
):
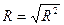 ,
,
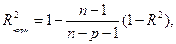
где n – число наблюдений (n=12), p – число регрессоров (факторов) в уравнении, в нашем случае p=2).
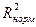 чувствителен к увеличению числа регрессоров и уменьшению числа наблюдений, чем больше факторов включено в модель и чем меньше число наблюдений, тем больше различия между множественным коэффициентом детерминации и скорректированной его величиной.
чувствителен к увеличению числа регрессоров и уменьшению числа наблюдений, чем больше факторов включено в модель и чем меньше число наблюдений, тем больше различия между множественным коэффициентом детерминации и скорректированной его величиной.
Сначала найдем среднее значение 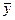 , определим векторы
, определим векторы 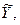
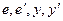 и объемы вариации
и объемы вариации 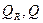 через произведение векторов, а затем рассчитаем показатели связи:
через произведение векторов, а затем рассчитаем показатели связи:

Между коэффициентом детерминации и скорректированным коэффициентом существуют различия (1,6%), так как число наблюдений не велико. Поскольку различия не столь существенны, можно использовать R2 и R для оценки тесноты связи. Множественный коэффициент корреляции (R = 0,963) свидетельствует об очень тесной связи между факторами и результатом, множественный коэффициент детерминации показывает, что 92,7 % вариации ВРП на душу населения связано с включенными в модель факторами. Полученные выводы следует оценить: насколько они существенны для генеральной совокупности, поскольку мы получили лишь выборочные показатели связи и выборочное уравнение регрессии.
4.3 Дадим оценку значимости уравнения в целом, условного начала и коэффициентов чистой регрессии.
Оценка значимости уравнения в целом проводится на основе дисперсионного анализа.
Предположим, что уравнение не значимо для генеральной совокупности (Н0: 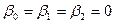 ) в качестве альтернативной гипотезы выдвинем предположение о значимости уравнения (НА:
) в качестве альтернативной гипотезы выдвинем предположение о значимости уравнения (НА: 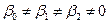 ). Проверим эти гипотезы на 5% уровне значимости. В качестве критерия выберем критерий F-Фишера, определим его фактическое значение:
). Проверим эти гипотезы на 5% уровне значимости. В качестве критерия выберем критерий F-Фишера, определим его фактическое значение:
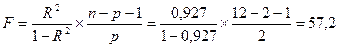 .
.
Сравним его с критическим значением 
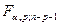 , которое можно найти, используя встроенную функцию FРАСПОБР(
, которое можно найти, используя встроенную функцию FРАСПОБР( 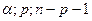 ). В нашем случае:
). В нашем случае: 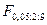 =FРАСПОБР(0,05;2;9)=4,3.
=FРАСПОБР(0,05;2;9)=4,3.
Поскольку фактическое значение превышает критическое, принимаем гипотезу о значимости уравнения в целом.
Можно также найти значимость критерия (фактического значения), используя функцию FРАСП ( 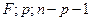 ). Критерий значим уже при 0,0008% области, что гораздо меньше принятой нами 5%.
). Критерий значим уже при 0,0008% области, что гораздо меньше принятой нами 5%.
Следовательно, уравнение в целом значимо, но возможно не значим какой-либо из его параметров для генеральной совокупности.
Выдвинем рабочую гипотезу о равенстве нулю всех параметров уравнения в генеральной совокупности и альтернативную ей:
H0: HА:
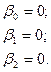
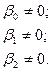
Гипотезы проверим на 5% уровне значимости.
Для проверки гипотез воспользуемся критерием t-Стьюдента, фактические значения которого определим по формуле:
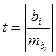 ,
,
где 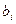 – элемент матрицы B, т.е. параметр выборочного уравнения регрессии, соответственно i принимает значения 0, 1, 2;
– элемент матрицы B, т.е. параметр выборочного уравнения регрессии, соответственно i принимает значения 0, 1, 2;

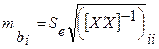 ,
,
где 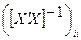 – диагональный элемент обратной матрицы, в нашем случае элементы с индексами 00, 11 и 22 (необходимы для нахождения ошибок параметров b0, b1, b2 ) выделены серым цветом:
– диагональный элемент обратной матрицы, в нашем случае элементы с индексами 00, 11 и 22 (необходимы для нахождения ошибок параметров b0, b1, b2 ) выделены серым цветом:


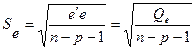 .
.
В нашей модели среднее квадратическое отклонение остатка будет равно:
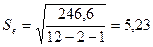 .
.
Фактическое значение критерия t-Стьюдента, его значимость и критическое значение приведены в табл.2. Напомним, что значимость фактического значения критерия можно определить, используя функцию СТЬЮДРАСП(t (фактическое значение);n-p-1;p), найти критическое значение – СТЬЮДРАСПОБР( 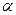 ;n-p-1).
;n-p-1).
2. Оценка значимости. Точечная и интервальная оценки параметров уравнения регрессии
| Пара-метры | Выборочная оценка параметров | Диагональный элемент обратной матрицы (Х'Х)-1 | Средняя ошибка, m | Значение критерия t-Стьюдента | Значимость фактического значения критерия t-Стьюдента | Доверительный интервал | ||
| факти-ческое | крити-ческое | нижняя граница | верхняя граница | |||||
| в0 | -226,0 | 109,187601482 | 54,6956 | 4,13 | 2,26 | 0,00255 | -349,7 | -102,2 |
| в1 | 0,004 | 0,000000008 | 0,0005 | 7,56 | 2,26 | 0,00003 | 0,003 | 0,005 |
| в2 | 3,935 | 0,028235156 | 0,8796 | 4,47 | 2,26 | 0,00155 | 1,945 | 5,925 |
Как видно из табл. 2 все параметры оказались значимы на уровне от 0,003% до 0,255%, а задавали мы 5% уровень. Следовательно, можно дать точечную и интервальную оценку параметрам в генеральной совокупности.
Точечная оценка позволяет предположить, что генеральное уравнение будет иметь параметры:
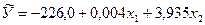 , при соответствующих размерах средних ошибок (табл. 2).
, при соответствующих размерах средних ошибок (табл. 2).
Проведем интервальную оценку:
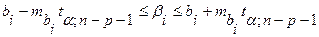 .
.
Для нашей модели с уровнем вероятности суждения 95% можно утверждать, что параметры генерального уравнения множественной регрессии попадут в интервалы:
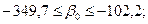
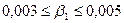 ;
;
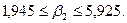
Поскольку все параметры уравнения регрессии оказались значимыми, возможна их интерпретация. Коэффициенты чистой регрессии показывают, что:
- при увеличении уровня инвестиций на душу населения на 1 рубль уровень ВРП возрастет в среднем на 4 рубля (с уровнем доверия 95% можно утверждать, что он возрастет от 3 до 5 рублей), при условии, что уровень экономической активности останется зафиксированным на среднем уровне;
- при увеличении уровня экономической активности на 1%, ВРП на душу населения возрастет в среднем почти на 4 тыс. руб. (с уровнем доверия 95% можно утверждать, что он возрастет от 2 до 6 тысяч рублей), если второй фактор не изменится.
Условное начало интерпретации не подлежит.
Следует отметить, что модель можно использовать в целях прогнозирования, поскольку при высоком коэффициенте детерминации все параметры уравнения оказались значимы.
5. Построим модель с использованием инструмента «Регрессия», предусмотрев вывод остатков, в итоге получим выходные данные:
| ВЫВОД ИТОГОВ | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,963 | |||||
| R-квадрат | 0,927 | 
| ||||
| Нормированный R-квадрат | 0,911 | |||||
| Стандартная ошибка | 5,23 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 3132,5 | 1566,2 | 57,2 | 0,000008 | ||
| Остаток | 246,6 | 27,4 | ||||
| Итого | 3379,1 | |||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | -226,0 | 54,6956 | -4,13 | 0,00255 | -349,7 | -102,2 |
| Переменная X 1 | 0,004 | 0,0005 | 7,56 | 0,00003 | 0,003 | 0,005 |
| Переменная X 2 | 3,935 | 0,8796 | 4,47 | 0,00155 | 1,945 | 5,925 |
| ВЫВОД ОСТАТКА | 
| |||||
| Наблюдение | Предсказанное Y | Остатки | ||||
| 36,8 | -6,0 | |||||
| 36,8 | 1,5 | |||||
 3 3
| 24,8 | -3,1 | ||||
| 43,3 | -0,7 | |||||
| 32,8 | -3,8 | |||||
| 78,2 | 0,6 | |||||
| 52,5 | 2,7 | |||||
| 54,1 | -4,8 | |||||
| 45,1 | 2,8 | |||||
| 31,1 | 11,9 | |||||
| 76,1 | 0,3 | |||||
| 38,1 | -1,6 |
Проводя сравнение всех определенных ранее в процессе анализа величин с полученными в автоматическом режиме, приходим к выводу о правильности проведенных расчетов.
6. Определим прогнозное значение ВРП на душу населения. Предположим, что в изучаемом округе удастся повысить уровень вложений с 6290 руб. до 7000 (в трех регионах уже достигнуты и более высокие уровни), т.е. запланируем прирост на уровне 10-11%; а уровень экономической активности увеличить на 1 % по сравнению со средним, т.е. предположим, что он достигнет 64,3%.
Прогнозные значения запишем в виде матрицы:
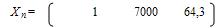 , тогда
, тогда 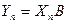 =52,4 тыс. руб. в расчете на душу населения, что на 6,6 тыс. руб., или 14,5%, больше достигнутого среднего уровня. И если давать точечную оценку прогноза для генеральной совокупности, то величина средней ошибки составит:
=52,4 тыс. руб. в расчете на душу населения, что на 6,6 тыс. руб., или 14,5%, больше достигнутого среднего уровня. И если давать точечную оценку прогноза для генеральной совокупности, то величина средней ошибки составит:
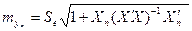 .
.
Последовательно найдем матрицы:
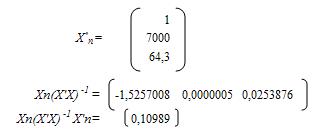
Тогда 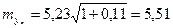 тыс. руб. Средняя ошибка прогноза велика вследствие большой дисперсии остатка, на величину которой в свою очередь оказывает влияние число степеней свободы, которое равно всего 9 регионам. Поэтому при увеличении числа наблюдений качество прогноза повысится.
тыс. руб. Средняя ошибка прогноза велика вследствие большой дисперсии остатка, на величину которой в свою очередь оказывает влияние число степеней свободы, которое равно всего 9 регионам. Поэтому при увеличении числа наблюдений качество прогноза повысится.
Доверительный интервал прогноза имеет вид:
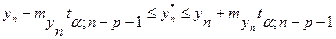 .
.
Прогнозное значение в генеральной совокупности при уровне вероятности суждения 95% будет находиться в пределах:
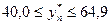 , т.е. от 40 до 65 тыс. руб.
, т.е. от 40 до 65 тыс. руб.
| <== предыдущая лекция | | | следующая лекция ==> |
| Татари і башкири | | | Політичні процеси поклали початок масовим репресіям проти радянських людей. |