Так звану Версальсько-Вашингтонську систему.

Дата добавления: 2015-08-31; просмотров: 670

Практическая значимость уравнения множественной регрес­сии оценивается с помощью показателя множественной корре­ляции и его квадрата - коэффициента детерминации.

Показатель множественной корреляции характеризует тесно­ту связи рассматриваемого набора факторов с исследуемым при­знаком, или, иначе, оценивает тесноту совместного влияния факторов на результат.

Независимо от формы связи показатель множественной кор­реляции может быть найден как индекс множественной корре­ляции:

где σ²_у — общая дисперсия результативного признака;

σ²_ост - остаточная дисперсия для уравнения y =f(x₁ , x₂,..., x_p).

Расчет индекса множественной корреляции предполагает оп­ределение уравнения множественной регрессии и на его основе остаточной дисперсии:

Можно пользоваться следующей формулой индекса множе­ственной корреляции:

При линейной зависимости признаков формула индекса кор­реляции может быть представлена следующим выражением:

где β_xi - стандартизованные коэффициенты регрессии;

r_уxi -парные коэффициенты корреляции результата с каждым фактором.

Формула индекса множественной корреляции для линейной регрессии получила название линейного коэффициента множест­венной корреляции,или, что то же самое, совокупного коэффици­ента корреляции.

В рассмотренных показателях множественной корреляции (индекс и коэффициент) используется остаточная дисперсия, ко­торая имеет систематическую ошибку в сторону преуменьшения, тем более значительную, чем больше параметров определяется в уравнении регрессии при заданном объеме наблюдений n. Если число параметров при xjравно т и приближается к объему на­блюдений, то остаточная дисперсия будет близка к нулю и коэф­фициент (индекс) корреляции приблизится к единице даже при слабой связи факторов с результатом. Для того чтобы не допус­тить возможного преувеличения тесноты связи, используется скорректированный индекс (коэффициент) множественной кор­реляции.

Скорректированный индекс множественной корреляции со­держит поправку на число степеней свободы, а именно остаточ­ная сумма квадратов делится на число степеней свободы остаточной вариации (n - т - 1), а общая сумма квадра­тов отклонений - на число степеней свободы в целом по совокупности (n - 1).

Формула скорректированного индекса множественной детер­минации имеет вид:

где т - число параметров при переменных х;

n - число наблюдений.

Поскольку , то величину скорректированного индекса детерминации можно представить в виде

Чем больше величина m, тем сильнее различия и R².

Для линейной зависимости признаков скорректированный коэффициент множественной корреляции определяется по той же формуле, что и индекс множественной корреляции, т.е. как корень квадратный из . Отличие состоит лишь в том, что в линейной зависимости под m подразумевается число факторов, включенных в регрессионную модель, а в криволинейной зависимости m – число параметров при x и их преобразованиях (x², ln х и др.), которое может быть больше числа факторов как экономических переменных. Так, если у=f(х₁, х₂), то для линейной регрессии m=2, а для регрессии вида

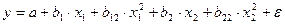
число параметров при х равно 4, т.е. m=4. При заданном объеме наблюдений при прочих равных условиях с увеличением числа независимых переменных (параметров) скорректированный коэффициент множественной детерминации убывает. Его величина может стать и отрицательной при слабых связях результата с факторами. В этом случае он должен считаться равным 0. При небольшом числе наблюдений скорректированная величина коэффициента множественной детерминации R² имеет тенденцию переоценивать долю вариации результативного признака, связанную с влиянием факторов, включенных в регрессионную модель.

Парные коэффициенты корреляции.Для измерения тесноты связи между двумя из рассматриваемых переменных(без учета их взаимодействия с другими переменными) применяются парные коэффициенты корреляции. Методика расчета таких коэффициентов и их интерпретации аналогичны линейному коэффициенту корреляции в случае однофакторной связи.

Частные коэффициенты корреляции. Однако в реальных условиях все переменные, как правило, взаимосвязаны. Теснота этой связи определяется частными коэффициентами корреляции, которые характеризуют степень влияния одного из аргументов на функцию при условии, что остальные независимые переменные закреплены на постоянном уровне. В зависимости от количества переменных, влияние которых исключается (элиминируется), частные коэффициенты корреляции могут быть различного порядка. При исключении влияния одной переменной получаем частный коэффициент корреляции первого порядка; при исключении влияния двух переменных – второго порядка и т.д. Парный коэффициент корреляции между функцией и аргументом обычно не равен соответствующему частному коэффициенту.

Частный коэффициент корреляции первого порядка между признаками у и х₁ при исключенном влиянии признака х₂ вычисляется по формуле

где r – парные коэффициенты корреляции между соответствующими признаками.

Для уравнения регрессии с тремя факторами частные коэффициенты корреляции второго порядка определяются на основе частных коэффициентов корреляции первого порядка. Так по уравнению

возможно исчисление трех частных коэффициентов корреляции второго порядка:

каждый из которых определяется по рекуррентной формуле. Например, при i = 1 имеем формулу для расчета r_yx1*x2x3 , а именно

В эконометрике частные коэффициенты корреляции обычно не имеют самостоятельного значения. В основном их используют на стадии формирования модели, в частности в процедуре отсева факторов. Так, строя многофакторную модель, например, мето­дом исключения переменных, на первом шаге определяется урав­нение регрессии с полным набором факторов и рассчитывается матрица частных коэффициентов корреляции. На втором шаге отбирается фактор с наименьшей и несущественной по t-крите­рию Стьюдента величиной показателя частной корреляции. Ис­ключив его из модели, строится новое уравнение регрессии. Про­цедура продолжается до тех пор, пока не окажется, что все част­ные коэффициенты корреляции существенно отличаются от ну­ля. Если исключен несущественный фактор, то множественные коэффициенты детерминации на двух смежных шагах построе­ния регрессионной модели почти не отличаются друг от друга, т. е. R²_p+1≈ R²_p где p — число факторов.

Методические рекомендации к лабораторной работе.