Утворення міжнародних організацій.

Дата добавления: 2015-08-31; просмотров: 772

Как и в парной зависимости, возможны разные виды уравне­ний множественной регрессии: линейные и нелинейные.

Ввиду четкой интерпретации параметров наиболее широко используются линейная и степенная функции. В линейной мно­жественной регрессии парамет­ры при xназываются коэффициентами «чистой» регрессии.Они характеризуют среднее изменение результата с изменением соот­ветствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.

Пример.Предположим, что зависимость расходов на продук­ты питания по совокупности семей характеризуется следующим уравнением:

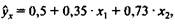
где у — расходы семьи за месяц на продукты питания, тыс. руб.;

х₁ — месячный доход на одного члена семьи, тыс. руб.;

х₂ - размер семьи, человек.

Анализ данного уравнения позволяет сделать выводы — с рос­том дохода на одного члена семьи на 1 тыс. руб. расходы на пита­ние возрастут в среднем на 350 руб. при том же среднем размере семьи. Иными словами, 35 % дополнительных семейных расхо­дов тратится на питание. Увеличение размера семьи при тех же ее доходах предполагает дополнительный рост расходов на питание на 730 руб. Параметр a не подлежит экономической интерпре­тации.

Выбор форм связи затрудняется тем, что, используя математический аппарат, теоретически зависимость между признаками может быть выражена большим числом различных функций.

Выбор типа уравнения осложнен тем, что для любой формы зависимости выбирается целый ряд уравнений, которые в определенной степени будут описывать эти связи. Некоторые предпосылки для выбора определенного уравнения регрессии получают на основе анализа предшествующих аналогичных исследований или на базе анализов подобных работ в смежных отраслях знаний. Поскольку уравнение регрессии строится главным образом для объяснения и количественного выражений взаимосвязей, оно должно хорошо отражать сложившиеся между исследуемыми факторами фактические связи.

Наиболее приемлемым способом определения вида исходного уравнения регрессии является метод перебора различных уравнений.

Сущность данного метода заключается в том, что большое число уравнений (модели) регрессии, отобранных для описания связей какого-либо социально-экономического явления или процесса, реализуется на ЭВМ с помощью специально разработанного алгоритма перебора с последующей статистической проверкой, главным образом, на основе t – критерия Стьюдента и F – критерия Фишера – Снедекора.

Способ перебора является достаточно трудоемким и связан с большим объемом вычислительных работ.

Практика построения многофакторных моделей взаимосвязи показывает, что все реально существующие зависимости между социально экономическими явлениями можно описать используя пять типов моделей:

1) Линейная:

2) Степенная

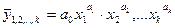
3) Показательная

4) Параболическая

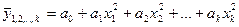
5) Гиперболическая

Основное значение имеют линейные модели в силу простоты и логичности их экономической интерпретации. Нелинейные формы зависимости приводятся к линейным путем линеаризации.

Параметры уравнения множественной регрессии оценивают­ся, как и в парной регрессии, методом наименьших квадратов (МНК). При его применении строится система нормальных уравнений, решение которой и позволяет получить оценки пара­метров регрессии.

Так, для уравнения у = а + b₁ · х₁ + b₂ · х₂ + ··· + b_р · х_р + ε сис­тема нормальных уравнений составит:

Ее решение может быть осуществлено методом определителей:

где Δ — определитель системы;

Δа, Δb₁,..., Δb_p — частные определители.

Возможен и иной подход к определению параметров множе­ственной регрессии, когда на основе матрицы парных коэффи­циентов корреляции строится уравнение регрессии в стандарти­зованном масштабе:

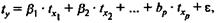
где — стандартизованные переменные:

для которых среднее значение равно нулю:

а среднее квадратическое отклонение равно единице:

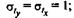
β -стандартизованные коэффициенты регрессии.

Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, после соответствующих преобра­зований получим систему нормальных уравнений вида

Решая ее методом определителей, найдем параметры — стан­дартизованные коэффициенты регрессии (β-коэффициенты).

Стандартизованные коэффициенты регрессии показывают, на сколько сигм изменится в среднем результат, если соответст­вующий фактор x_j, изменится на одну сигму при неизменном среднем уровне других факторов. В силу того, что все перемен­ные заданы как центрированные и нормированные, стандартизо­ванные коэффициенты регрессии β_j сравнимы между собой. Сравнивая их друг с другом, можно ранжировать факторы по си­ле их воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от ко­эффициентов «чистой» регрессии, которые несравнимы между собой.

Пример.Пусть функция издержек производства у (тыс. руб.) характеризуется уравнением вида

у = 200+ 1,2·x₁ + 1,1 ·x₂ + ε,

где x₁ — основные производственные фонды (тыс. руб.);
х₂ — численность занятых в производстве (чел.).

Анализируя его, мы видим, что при той же занятости дополнительный рост стоимости основных производственных фондов на 1 тыс. руб. влечет за собой увеличение затрат в среднем на 1,2 тыс. руб., а увеличение численности занятых на одного человека способствует при той же технической оснащенности предприятий росту затрат в среднем на 1,1 тыс. руб. Однако это не означает, что фактор х₁ оказывает более сильное влияние на издержки производства по сравнению с фактором х₂. Такое сравнение воз­можно, если обратиться к уравнению регрессии в стандартизованном масштабе. Предположим, оно выглядит так:

Это означает, что с ростом фактора х₁ на одну сигму при не­изменной численности занятых затраты на продукцию увеличи­ваются в среднем на 0,5 сигмы. Так как β₁< β₂ (0,5 < 0,8), то мож­но заключить, что большее влияние оказывает на производство продукции фактор х₂, а не x₁, как кажется из уравнения регрессии в натуральном масштабе.