Тригер на біполярних транзисторах

Дата добавления: 2014-12-06; просмотров: 740

Широкое применение на предприятиях машиностроения и других отраслей промышленности функционально-стоимостного анализа требует постоянного совершенствования методологических подходов и приемов, используемых в процессе его проведения. Особенно важное значение это имеет по отношению к одной из ключевых процедур ФСА – анализу и классификации функций. В методике ФСА, созданной Л. Майлсом эта процедура сводится к формулированию функций объекта анализа и их подразделению на основные, вспомогательные, ненужные, эстетические и др. Существующий подход не позволяет достаточно четко установить взаимосвязи между различными функциями, которые рассматриваются и анализируются изолированно, в отрыве друг от друга.

За рубежом неоднократно предпринимались попытки модификации методики анализа и классификации функций с целью сделать её более целенаправленной и формализованной. Наиболее удачной оказалась методика систематизированного анализа функций (FAST), основы которой были разработаны Чарльзом Байтуэем в 1965г. (В переводе на русский язык FAST – методика систематизированного анализа функций).

Методика FAST предусматривает построение для каждого конкретного случая функциональной модели или диаграммы функций, по внешнему виду напоминающие сетевой график. В СШа и других зарубежных странах методика FAST быстро получила "права гражданства", она все более широко применяется при проведении ФСА. В отечественной литературе сущность методики FAST и правила построения диаграмм впервые были изложены в аналитическом обзоре Е.А.Гампом и л.м. Сорокиной, опубликованном в ИНФОРМЭЛЕКТРО в 1978 г. /6/.

концепции, лежащие в основе методики, базируются на применении принципов детерминированной логики в процессе анализа и классификации функций. методика позволяет не только выявить и сформулировать основные и вспомогательные функции, а также так называемые функции более высокого и более низкого уровней, но и проверить правильность проведенной классификации и принятых формулировок, установить взаимосвязь между функциями. Для определения правильности местоположения каждой функции на диаграмме используется цепочка логически связанных ответов на ряд вопросов. Существует несколько модификаций методики FAST, в которых используются различные наборы таких вопросов. Число вопросов может быть 2, 3 ,9 и т.д. В простейшем случае по отношению к каждой функции задаются два вопроса: "Как?", "Почему?" ("Зачем?")."Как осуществляется данная функция?" и "Почему (зачем) осуществляется данная функция?". Может быть также задан и третий вопрос "Когда осуществляется данная функция?".

Для построения диаграммы необходимо выполнить следующее:

На небольших карточках записываются все функции анализируемого объекта. Из этих карточек выбирается карточка с той функцией, которая, по мнению специалистов, является основной. Из оставшихся карточек выбираются карточки с функцией более высокого уровня по отношению к основной функции. Эта функция должна отвечать на вопрос "Почему осуществляется данная (основная) функция?". На диаграмме карточка с этой функцией всегда располагается слева от основной функции (Рис. 4.1).

Рис. 4.1. Анализ функций с помощью вопросов "Как?" и "Почему?"

Далее отбирается карточка с функцией, которая является функцией более низкого уровня по отношению к основной. Эта функция должна быть ответом на второй вопрос " Как осуществляется данная (основная) функция?". Функция более низкого уровня всегда располагается на диаграмме справа от анализируемой функции. Последовательно задавая вопросы по отношению ко всем функциям, можно построить полную диаграмму для анализируемого объекта.

Основные правила построения диаграммы формулируются следующим образом:

1.Рамки проблемы, подлежащей исследованию, ограничиваются на диаграмме двумя вертикальными пунктирными линиями (Рис. 4.2). Функции, которые являются объектом анализа, располагаются между этими двумя граничными линиями. Левая граничная линия находится между анализируемой основной функцией и основной функцией более высокого уровня. Она расположена слева от левой граничной линии и не является объектом анализа.

2. На всех диаграммах FAST так называемые функции критического пути располагаются на горизонтальной линии, пересекающей граничные линии. Каждая из этих функций показывает "как" или почему" осуществляется какая-нибудь другая расположенная рядом функция критического пути.

3. На линии критического пути располагаются только основные, необходимые вспомогательные функции и функции более высокого и более низкого уровней.

4. Основная анализируемая функция всегда располагается непосредственно справа от левой граничной линии.

5. Все остальные функции критического пути располагаются справа от основной анализируемой функции.

6. Функции более низкого уровня всегда располагаются справа от правой граничной линии.

7. Все вспомогательные функции, не являющиеся функциями критического пути, располагаются либо над, либо под функциями критического пути. Это могут быть необходимые вспомогательные функции, эстетические функции или ненужные функции.

8. Те функции, которые осуществляются одновременно с какой-либо функцией критического пути или обусловлены ею, располагаются на диаграмме под этой функцией.

9. Функции, которые осуществляются объектом анализа постоянно, располагаются над линией критического пути в верхнем правом углу диаграммы.

10. целевые ориентиры располагаются в правом верхнем углу диаграммы над линией критического пути, они указывают технические характеристики или показатели, которые необходимо достигнуть.

11. Функции одноразового действия располагаются над линией критического пути в центре диаграммы.

12. Для установления приоритетности функций, их взаимосвязи (а также для проверки правильности их расположения на диаграмме) рекомендуется пользоваться логическими тестами, основанными на вопросах: "Как?", "Почему?", "Когда?".

13. С помощью первого теста получают ответ на вопрос: "Как осуществляется данная функция?". Вопрос должен состоять из трех слов: слова "как", глагола и существительного. Ответ на этот вопрос должен содержаться в формулировке функции, расположенной непосредственно справа от рассматриваемой функции. Если эта функция не дает ответа на поставленный вопрос, значит или функция неправильно сформулирована, или она неправильно размещена на диаграмме.

14. Второй тест проводится аналогичным образом, но в противоположном направлении. Вопрос: "Почему осуществляется данная функция?". Этот вопрос состоит из слова "почему", глагола и существительного. ответ должен содержаться в формулировке функции, расположенной непосредственно слева от рассматриваемой функции.

15. При проведении третьего теста в отношении каждой функции ставится вопрос: "Когда осуществляется данная функция?" ответы на этот вопрос содержат формулировки тех функций, которые осуществляются одновременно с той или иной функцией критического пути или обусловлены ею. Вспомогательные функции, формулировки которых получаются при ответе на этот вопрос, соединяются с соответствующими функциями критического пути пунктирными линиями.

16. Ответы на вопросы всех трех указанных выше тестов должны быть логичными и не противоречить здравому смыслу.

17. На линии критического пути располагаются те функции, которые должны быть обязательно осуществлены для реализации основной анализируемой функции. Все остальные функции, располагаемые на диаграмме FAST, являются как бы подчиненными по отношению к функциям критического пути.

18.На диаграмму FAST можно дополнительно нанести наименования деталей, выполняющих ту или иную функцию, помещая их непосредственно под соответствующими формулировками функций. Примерная диаграмма FAST коллекторного магнитоэлектрического двигателя постоянного тока представлена на рис. 4.3.

Ниже рассматриваются основные понятия и формулировки диаграммы FAST /7/.

Степень охвата анализируемой проблемы (или отдельного ее аспекта) характеризуется функциями, расположенными на диаграмме между двумя граничными вертикальными пунктирными линиями.

Функция высшего уровня. Цель, которую должна выполнить основная функция (т.е. объект анализа), называется функцией высшего уровня. На диаграмме она находится между левой граничной линией и основной функцией. Любая функция, находящаяся на диаграмме слева от любой другой функции, является функцией более высокого уровня.

Функция низшего уровня. Эта функция, находящаяся справа от правой граничной линии, является как бы первопричиной существования анализируемого объекта и называется функцией низшего уровня. Любая функция, находящаяся на диаграмме справа от любой другой функции, является функцией более низкого уровня.

Основная функция. Эта функция, находящаяся непосредственно слева от левой граничной линии, характеризует цель, для реализации которой предназначен объект анализа.

Концепция. Все функции, находящиеся справа от основной функции, описывают подход, выбранный для реализации основной функции, или концепцию, которая либо отражает существующее положение, либо формируется на базе внесенных аналитиками новых предложений. А какой подход (концепцию) выбрать (уже существующий или новый, предложенный), зависит от характера исследуемой проблемы и решения группы, проводящей анализ.

Целевые ориентиры или технические условия. Это конкретные параметры или ограничения, которые должны быть достигнуты и соблюдены для реализации функции высшего уровня. Хотя сами по себе целевые ориентиры и технические условия не являются функциями, они могут повлиять на концепцию, выбранную с целью наиболее эффективной реализации основной функции и удовлетворения требований потребителя. Использование целевых ориентиров или технических условий в процессе построения диаграмм FAST не является обязательным.

Функции критического пути. Любая функция, формулировка которой умещается в логическую схему, определяемую вопросами "как" или "почему?", является функцией критического пути.

Если линия, выходящая из прямоугольника с формулировкой какой-либо функции, подходит к основной функции в направлении, определяемом вопросом "почему?", она называется линией главного критического пути. Во всех остальных случаях, когда на линии, проходящей в направлении вопроса "почему?", будут находиться независимые (вспомогательные) функции, она называется линией малого критического пути. Вспомогательные функции всегда являются второстепенными, они служат либо для достижения требований, указанных для основных функций в целевых ориентирах или технических условиях, либо непосредственно для реализации основных функций. Формулировки независимых функций (находящихся над линией критического пути) и действий (расположенных под ней) получаются в результате постановки вопроса "когда?".

Зависимые функции. Начиная с первой функции, расположенной справа от основной, каждая последующая функция "зависит" от функции, находящейся непосредственно слева от нее, т.е. от функции более высокого уровня. Эта зависимость становится еще более очевидной, когда задается вопрос "как?" и следуют в направлении, определяемом этим вопросом.

Независимые (вспомогательные) функции. Эти функции не зависят от какой-либо другой функции или от способа, выбранного для реализации этой функции. Независимые функции располагаются над функциями критического пути. Они считаются вспомогательными по отношению к анализируемой проблеме и к функциям критического пути.

Функция. Конечный результат или цель, для достижения или реализации которой предназначается объект анализа (им может быть предмет, процесс или действие). Этот результат или цель формулируется двумя словами: глаголом и существительным.

Действия. Способ, выбранный для реализации функции (или ряда функций).

Если рассматривать диаграмму FAST с точки зрения системного анализа, может показаться, что она строится в обратном направлении, поскольку при схематическом изображении системы "вход", как правило, расположен слева, а "выход" – справа. Однако следует иметь в виду, что в случае изменения способа, выбранного для реализации той или иной функции критического пути, изменение претерпевают все функции, находящиеся справа от этой функции, т.е. (если говорить на языке FAST) – все зависимые функции. Следовательно, направления "как?" (слева направо) и "почему?" (справа налево) полностью соответствуют логике FAST.

Прежде чем приступить к комплектованию рабочей группы для построения диаграммы FAST, ее будущий руководитель досконально изучает все аспекты рассматриваемой проблемы. Если такая группа уже имеется, после изучения проблемы ее состав может быть соответствующим образом скорректирован. При подборе состава группы рекомендуется руководствоваться следующими соображениями: в ней должны быть специалисты, имеющие отношение ко всем частям диаграммы FAST, а именно к правой ее части, т.е. к функции низшего уровня, к средней части, расположенной между двумя вертикальными граничными линиями, и к левой части, т.е. к функции высшего уровня.

Так, на предприятии, занимающемся разработкой и производством изделий машиностроения, в рабочую группу ФСА должны входить представители производственных служб (левая часть диаграммы – выход системы), представители служб маркетинга и сбыта (правая часть диаграммы – вход системы) и конструкторских служб (средняя часть диаграммы, расположенная между вертикальными граничными линиями).

Перед тем, как приступить к построению диаграммы FAST, все члены укомплектованной рабочей группы должны прийти к единому мнению относительно формулировки проблемы, подлежащей исследованию. Это очень важно по следующим причинам:

1. Внимание всех членов группы должно быть сконцентрировано на основных, а не на второстепенных аспектах проблемы.

2. Совместными усилиями легче правильно сформулировать проблему, которая должна обязательно включать в себя формулировки основной функции высшего уровня.

Перед тем как группа приступает к непосредственному построению диаграммы FAST, рекомендуется задать ее членам три вопроса.

1. Что представляет собой рассматриваемая проблема?

2. Почему Вы считаете это проблемой?

Этот вопрос преследует две цели:

а) он позволяет выявить наиболее вероятные причины возникновения проблемы и степень важности ее решения;

б) слово "почему?" в этом вопросе определяет еще и направление (). Поэтому с помощью этого вопроса можно проверить правильность формулировок основной функции и функции высшего уровня, сформулированных при постановке первого вопроса.

3. Почему Вы полагаете, что есть необходимость в решении этой проблемы?

Ответ на этот вопрос должен подтвердить, дополнить или видоизменить ответ на предыдущий вопрос.

С помощью диаграммы FAST можно произвести оценку стоимости функции критического пути и вспомогательных функций. для этого функции оцениваются в стоимостном выражении, и производится суммирование функций. Это позволяет сразу же выявлять распределение стоимостей по функциям и областям диаграммы FAST, чтобы на творческой стадии ФСА определять те направления, по которым следует вести работу для сведения к минимуму излишних стоимостей, заложенных в той или иной функциональной зоне.

4.3. Компьютерная графика и экономико-математические методы при проведении функционально-стоимостного анализа

Компьютерная графика в настоящее время сформировалась как наука об аппаратном и программном обеспечении для разнообразных изображений от простых чертежей до реалистичных образов естественных объектов. Компьютерная графика используется почти во всех научных, инженерных и экономических исследованиях для наглядности восприятия и передачи информации. Конечным продуктом компьютерной графики является изображение. Это изображение может использоваться в различных сферах, например, оно может быть техническим чертежом, иллюстрацией с изображением детали в руководстве по эксплуатации, диаграммой или топограммой, проектным заданием или сетевым графиком.

В компьютерной графике рассматриваются следующие задачи:

1. Представление изображения.

2. Подготовка изображения к визуализации.

3. Создание изображения.

4. Осуществление действий с изображением.

Под компьютерной графикой обычно понимают автоматизацию процессов подготовки, преобразования, хранения и воспроизведения графической информации с помощью ЭВМ. Под графической информацией понимаются модели объектов и их изображения.

Интерактивная компьютерная графика – это также использование ЭВМ для подготовки и воспроизведения изображений, но при этом пользователь имеет возможность оперативно вносить изменения в изображение непосредственно в процессе его воспроизведения, т.е. предполагается возможность работы с графикой в режиме диалога в реальном масштабе времени.

Интерактивная графика представляет собой важный раздел компьютерной графики, когда пользователь имеет возможность динамически управлять содержимым изображения, его формой, размером и цветом на поверхности дисплея с помощью интерактивных устройств управления.

Достоинства графики:

• наиболее естественные средства общения с ЭВМ;

• хорошо развитый двухмерный и трехмерный механизм распознавания образов позволяет очень быстро и эффективно воспринимать и обрабатывать различные виды данных;

• позволяет разумно использовать сочетания текста, статических и динамических изображений по сравнению со случаями, когда можно работать только с текстами. Это расширение существенно влияет на возможность понимать данные, выявлять тенденции и визуализировать существующие или воображаемые объекты при обработке.

Компьютерная или машинная графика применяется, когда исходной является информация не изобразительной природы, например, визуализация экспериментальных данных в виде графиков или гистограмм. Можно сказать, что компьютерная графика рисует, опираясь на формульные представления, и имеет набор средств.

Иллюстративное направление компьютерной графики можно понимать расширенно, начиная с представления результатов эксперимента и заканчивая созданием рекламных роликов. Во многих исследованиях инструментарий компьютерной графики начинает играть роль во многом подобную той, которую в свое время сыграл микроскоп.

Вывод изображения на экран компьютера является неотъемлемым, но всего лишь первым шагом на пути становления машинной графики. Довольно стремительно пройдя иллюстративный отрезок пути своего развития, компьютерная графика сосредоточилась на двух генеральных направлениях: придание изображению необходимой динамики и придание изображению необходимой реалистичности. Достижения компьютерной графики мы видим на экранах телевизоров, на рекламных заставках. Реклама в этом случае выступает как мощный стимул к развитию все более совершенного графического инструментария. Он существует в виде разнообразных графических пакетов, начиная от простеньких графических редакторов и заканчивая специальным программным обеспечением.

Из доступных универсальных графических редакторов можно назвать Компас-график, Paint, Corel Draw, Adobe Photoshop, AutoCAD, а также графические средства текстового редактора Word, позволяющие успешно и быстро осуществлять статистико-экономическое графирование.

Графические средства служат задаче наглядного изображения какого-либо организационного процесса. Любой график, как правило, включает в себя ряд обязательных элементов и линий, создающих пространственное представление об определенных предметах или процессах, основные и вспомогательные линии, а также надписи и знаки условного характера. Однако от графических изображений вообще, к которым относятся, например, географические карты или топографические схемы, график отличается тем, что он, как правило, не отображает самого предмета, а лишь выражает языком условного характера известную мысль об этом предмете.

В соответствии с этим и способы графирования (изображения) организационных чертежей можно разделить на две группы:

- геометрические (прямые линии, кривые и т.д.);

- идеографические (условные знаки, символы, надписи).

Обозначения первой группы выражают преимущественно количественные, а второй - качественные различия.

В процессе ФСА выделяют графические приемы, позволяющие:

- выявить или сформировать заново определенные связи, пропорции, структурные взаимоотношения (оргаграммы, схемы потоков информации, структурные и функциональные модели и др.);

- моделировать процессы по управлению (оперограммы, сетевые графики и др.);

- наиболее наглядно представить информацию (диаграммы, различные кривые);

- лучше осуществить контроль и учет (циклограммы, сетевые графики);

- производить расчетные операции, операции по нахождению различных нормативных данных и коэффициентов (шкалограммы, номограммы);

- группировать и классифицировать события и явления (классификационные схемы, морфологические матрицы).

Во всяком графике различают его содержание, т.е. что именно графиком выражается, и его форму – способы и приемы, с помощью которых содержание визуализируется.

Наряду со средствами компьютерной графики для проведении ФСА привлекаются экономико-математические и статистические методы, подразделяющиеся на субъективные, эвристические и использующие точные процедуры принятия решений. Хорошие результаты в данной ситуации дает соединение графических средств с экономико-математическими методами.

Субъективные методы:

коллективные балльные оценки;

частичное и полное попарное сравнение;

индексные коэффициенты и различные их модификации;

комбинирование сопоставления функций и их классификаций с разработкой соответствующих коэффициентов.

Эвристические методы:

метод Дельфи в различных модификациях;

эвристическое программирование;

анализ перекрестных взаимодействий в сочетании с методом Дельфи;

морфологический анализ и морфологическое программирование.

Точные методы:

нормативно-параметрический метод на базе статистических регрессионных моделей (регрессионный анализ);

оптимизация, представленная некоторыми задачами линейного программирования;

многомерный статистический анализ;

моделирование на основе генерирования случайных последовательных состояний марковских цепей;

проектирование оптимизационных экспериментов;

кластерный анализ и др.

Поскольку основная цель ФСА направлена на достижение наивысшей эффективности функционирования (полезности) изделий при минимуме затрат на их производство и эксплуатацию, то результаты деятельности должны отражаться, прежде всего, в ценообразовании. Опыт предприятий электротехнической промышленности показывает, что возникает необходимость использования нормативно-параметрических методов формирования рыночной цены. Становится возможным применение статистических методов для оценки связи между техническим уровнем и ценами изделия на мировом рынке. Тогда, исходя из опытных и прогнозируемых цен, а также коэффициентов соотношений технического уровня и цен зарубежных образцов, можно установить цену на новое изделие. Так, например, известна разработанная и опробованная методика параметрической оценки, основанная на построении математической модели и графическом представлении получившихся зависимостей.

Общая оценка выражена матрицей А, элементы которой а_ij – нормированные оценки n параметров m сравниваемых изделий, включая возможные экспертные оценки не измеряемых количественно свойств изделий, и вектором W_i, элементы которого w_i есть количественная оценка относительной весомости каждого из оцениваемых n параметров (коэффициенты значимости). В результате умножения получаем вектор V_j, каждый член которого представляет количественную комплексную оценку технического уровня j-го изделия. Таким образом, математическая модель имеет вид

. =

После выбора параметров на основе функциональной модели рассчитываются количественные оценки их относительных величин.

Имея информацию о ценах, можно построить на графике зависимость их от производственных оценок. На рис. 4.4 показана взаимосвязь между ценами и техническим уровнем изделий.

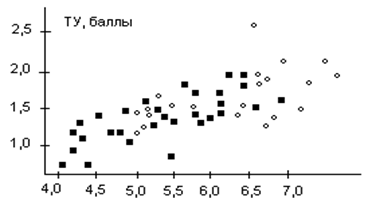
Рис. 4.4. Зависимость цены асинхронных двигателей от их технического уровня

- мощность двигателя 1000 кВт; ○ – мощность двигателя 1600 кВт.

При наборе данных более 50 возможно применение статистических методов для характеристики аналитической зависимости цен от технического уровня изделий. Исследование параметров и цен асинхронных двигателей показало, что такая зависимость выражается экспоненциальной кривой:

y = a · e^bx, (4.1)

где у – цена изделия;

x – технический уровень, рассчитанный методом наилучших оценок.

Цена нового изделия с использованием коэффициентов цен зарубежных образцов:

VC_n = VC_p · k_zr , (4.2)

где VC_p – цена первоначального изделия;

- коэффициент средних зарубежных цен, рассчитываемый по соотношению цен в ряде стран (k_crj ) по m параметрам.

Предположим, что первоначальный технический уровень изделия оценен в 65 баллов (А=65). Учитывая тенденции научно-технического развития и показатели лучших мировых образцов, выбирают вариант нового изделия с оценкой максимального уровня в 85 баллов (В=85). На основе графиков зависимости цен от технического уровня аналогичных изделий разных стран составляется таблица для расчета коэффициентов цен, куда заносятся данные об уровне цен, учитывающем их снижение против среднего на 12-14% (нижний уровень цен). На основе данных таблицы рассчитывается среднее значение коэффициента соотношения цен: k_zr = 1,866.

Анализ зависимости цен от оцениваемого технического уровня позволяет с достаточной степенью точности прогнозировать цену нового изделия, конкурентоспособного на мировом рынке.

В ходе проектирования электроизделий, отработки конструкции на технологичность, проведения ФСА возникает необходимость установления прямых затрат на изготовление изделий и их конструктивных элементов. Для определения размеров прямых затрат могут быть рекомендованы следующие методы: расчетно-аналитический, статистический, экспертный.

Расчетно-аналитический метод основан на использовании разработанной технической и экономической документации на детали и сборочные единицы изделия.

Стоимость материалов S_м рассчитывается по формуле:

S_м = В_расч Ц_м К_тз, (4.3)

где В_расч – чистый вес материала, кг;

Ц_м – цена 1 кг материала, руб.;

К_тз – коэффициент, учитывающий транспортно-заготовительные расходы, равный 1,03 - 1,05.

Заработную плату на выполнение операций, связанных с изготовлением детали или сборочной единицы, S_з.п. можно определить по формуле:

S_з.п. = t_оп l_т K_д.п., (4.4)

где t_оп – норма времени на выполнение комплекса операций, ч;

l_т – часовая тарифная ставка соответствующего разряда, р.;

K_д.п. – коэффициент, учитывающий дополнительную зарплату, отчисления на социальное страхование и доплату часового фонда.

Метод удельных показателей используется для определения и анализа себестоимости (цены) изделий, характеризующихся наличием одного основного параметра, величина которого и определяет общий уровень себестоимости (цены) изделия.

Удельные параметры определяются по формуле

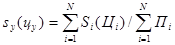, (4.5)

где s_y (ц_y) – удельная величина себестоимости (цены) на единицу основного параметра, р.;

i – номер изделия параметрического ряда;

N – количество изделий в исследуемом параметрическом ряду, шт.;

S_i (Ц_i) – себестоимость (цена) i - го изделия, р.;

П_i – значение основного параметра i - го изделия в соответствующих единицах измерения.

Применение метода удельных показателей предполагает наличие линейной зависимости между себестоимостью (ценой) и основным параметром изделия. Так, взаимосвязь между оптовой ценой и массой асинхронных электродвигателей, показанная на корреляционном поле (рис. 4.5), носит линейный характер. Чем более нелинейна функциональная зависимость между себестоимостью (ценой) и основным параметром изделия, тем выше ошибка в обосновании себестоимости (цены).

Таким образом, при решении каждой проблемы, возникающей при проведении функционально-стоимостного анализа, на практике используются различные экономико-математические методы, дающие хорошие результаты при совмещении с современными средствами компьютерной графики, позволяющей наглядно и подробно отображать получившиеся зависимости.