Правові основи утворення та функціонування підприємства

Дата добавления: 2014-12-06; просмотров: 699

Стремление к повышению точности измерений — одно из направлений постоянных метрологических работ. Наряду с этим следует особо подчеркнуть, что в повседневной практи­ке, в обиходе, в технических и технологических измерениях нужно стремиться не к наивысшей точности, цена которой, как правило, велика, а к целесообразной, оптимальной в смысле технико-экономических показателей.Основной целью метрологического обеспечения является не достиже­ние высокой точности, а гарантия единства и достоверности результатов измерений.

Научно-технический прогресс всегда обеспечивался адек­ватной точностью измерений. История науки содержит немало примеров того, как повышение точности измерений приводи­ло к фундаментальным научным открытиям. Многие техно­логические процессы в промышленности стали возможны только потому, что точность технических измерений достиг­ла соответствующего уровня. Под углом зрения обеспечения высоких темпов научно-технического прогресса и должен рассматриваться вопрос о точности измерений.

На рис. 160 приведены результаты анализа точности об­работки линейных размеров механических деталей электрон­ных изделий и оптических устройств за большой истори­ческий отрезок времени с прогнозом на обозримое буду­щее. Заштрихованная область относится к производству интегральных микросхем. Обобщение данных об их тополо­гических размерах и требованиях к допускам по совме­щению при литографических операциях показывает, что создание интегральных схем основывается на высокоточной обработке и прецизионных измерениях, точность которых примерно на порядок выше точности обработки обычных изделий, В перспективе ожидается создание нанотехнологии, представляющей комплексную технологию промышленной обработки изделий с точностью около 1 нм. При этом имеет­ся в виду объединение в единую взаимосогласованную систему многочисленных обрабатывающих инструментов, конт­рольно-измерительных и управляющих устройств с использо­ванием ЦЭВМ.

В режиме формообразования точность обработки традицион­ными способами принципиально ограничена областью 0,3 ... 1 нм, соответствующей размерам отдельных молекул и расстояни­ем в кристаллической решетке. Более отдаленная перспектива связана, поэтому с развитием молекулярной электроники. Приборы молекулярной элект­роники опираются на техноло­гию, использующую процессы само сборки. Подобная принципи­ально новая технология с атомной детализацией не может сравниваться с традиционной технологией формообразования и потребует развития нового подхода к оценке точности на молекулярном уровне.

Выход на уровни точности, близкие к предельно достижи­мой, ставит вопрос о потенци­альной точности измерений. Ответ на него зависит от уров­ня развития науки и техники.

Наиболее просто ответ на вопрос о потенциальной точ­ности измерений формулируется следующим образом: точ­ностьизмерений не может быть выше точности воспроиз­ведения единицы государственным первичным или специаль­нымэталоном (по определению). Никакое техническое уст­ройство не может рассматриваться в качестве измеритель­ного прибора, если ему установленным порядком не переда­на информация о размере единицы. А передача этой инфор­мации от государственного эталона всегда сопровождается потерей точности. Кроме того, точность измерений зависит от множества других факторов.

Не в последнюю очередь она зависит от количества апри­орной информации об объекте измерения. Чем ее больше, тем выше точность измерений. Априорная информация об объекте измерения позволяет сконструировать адекватную его модель, синтезировать оптимальную измерительную про­цедуру, правильно выбрать или синтезировать средство из­мерений. Важное значение для синтеза имеет априорная ин­формация о свойствах полезного сигнала и помех на входе средства измерений. Дефицит априорной информации огра­ничивает точность измерений и любые меры, направленные на его преодоление, приближают точность к потенциально возможной.

В свою очередь, как бы удачно не было синтезировано средство измерений оно не будет совершенным из-за недос­татков при изготовлении: конструктивных, технологических, дефектов комплектующих изделий, неточности настройки и регулировки, поддержания режимов работы и т.д. и т.п., а также вследствие нестабильности элементов и материалов, обусловленной старением, износом и другими причинами. Невозможно создать измерительный прибор, метрологи­ческие характеристики которого абсолютно точно соответ­ствовали бы проектным, а определение их эксперименталь­ным путем имеет ограниченную точность. Таким образом, несовершенство средств измерений и некоторая неопреде­ленность их реальных метрологических характеристик вно­сят свой вклад в ограничение точности результатов измере­ний.

На точности измерений сказываются также внешние и внутренние влияющие факторы. К внутренним относятся взаимные электромагнитные влияния элементов и их соеди­нений друг на друга, паразитные ТЭДС, тепловыделение, трение, акустическая эмиссия и т. д. Внешние влияющие фак­торы включают в себя изменение параметров окружающей среды (температуры, влажности, давления), напряжения в сети питания, наводки от расположенных поблизости электри­ческих машин и механизмов, всевозможные вибрации и сотря­сения, влияние электрических, магнитных, электромагнитных и гравитационных полей, ускорений и т. п. Их исключение, компенсация и учет в рабочих условиях измерений с помощью функций влияния далеки еще от совершенства.

В процессе измерения объект и средство измерений всту­пают во взаимодействие. В процессе этого взаимодействия средство измерений оказывает влияние на объект, прояв­ляющееся в изменении измеряемой величины. Результат измерения оказывается искаженным по сравнению с тем, каким он должен был бы быть, если бы средство изме­рений не влияло на объект. Как бы ни учитывалось это обстоятельство (а во многих случаях им просто пренебре­гают), оно снижает точность результата измерения.

Нельзя, наконец, не отметить и несовершенство самой измерительной процедуры (неточность установки прибора и снятия показаний, конечное время выполнения измере­ния, в течение которого происходит изменение внешних условий и ряда влияющих факторов, зависимость качест­ва измерения от квалификации оператора и многое другое). Это также обусловливает недостижимость потенциальной точности измерений.

Все вышеперечисленные факторы, влияющие на точность измерений, учитываются при разработке, стандартизации и аттестации методик выполнения измерений. В стандартах на методики (или в соответствующих разделах стандартов тех­нологических процессов, методов испытаний и контроля, методов и средств поверки) согласно ГОСТ 8.010—72 ука­зываются:

назначение и область применения стандартизованной методики выполнения измерений;

требования к средствам измерений и вспомогательным устройствам, необходимым для выполнения измерений (в том числе к уровню их автоматизации);

метод измерений;

порядок подготовки и выполнения измерений;

нормы на показатели точности измерений и зависимости, выражающие связи между этими показателями и всеми фак­торами, существенно влияющими на них при выполнении измерений, а также диапазоны значений влияющих величин, для которых эти зависимости справедливы. Указанные зави­симости могут быть представлены в виде таблиц,графиков, уравнений;

способы обработки результатов измерений и оценки по­казателей точности измерений;

требования к квалификации операторов;

требования к. технике безопасности.

В аттестатах на методики выполнения измерений указы­вают:

назначение и область применения методики;

типы и номера экземпляров средств измерений, используемых для проведения измерений. Номер экземпляра сред­ства измерений в аттестате не указывается, если значения показателей точности измерений, указанные в аттестате, оп­ределены с учетом возможности применения любого экземп­ляра средства измерений данного типа;

технические характеристики вспомогательных устройств, необходимых для выполнения измерений;

метод измерений;

порядок подготовки и выполнения измерений;

численные значения показателей точности измерений;

межповерочные интервалы для средств измерений и но­менклатуру нормативных документов, согласно которым должна проводиться их поверка;

требования к квалификации операторов;

требования техники безопасности.

Точность измерений во многом зависит также от алго­ритма обработки экспериментальных данных. Этим обуслов­лено требование аттестации алгоритмов.

В отдельных областях и видах измерении при совре­менной эталонной базе достигнута точность, обеспечивающая возможность выполнения измерений намолекулярном уровне. Формальным отражением этого служит появление пос­тоянной Больцмана k = 1,38 • 10 ^-23 Дж/К в выражениях, опи­сывающих влияющие факторы, с которыми нужно считаться. Частицы вещества — атомы, молекулы, а также электричес­кие заряды совершают непрерывные хаотические движения, интегральная интенсивность которых характеризуется тер­модинамической температурой Т. Чем интенсивнее движе­ния, называемые флюктуациями, тем выше абсолютная температура Т. Флюктуации создают шумовой эффект, ог­раничивающий точность измерения физических величин. Мощность шума Р_Ш определяется уравнением Найквиста:

,

где 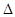f — ширина полосы пропускания прибора. Иногда это выражение дополняется спектральным коэффициентом N, учитывающим дробовый эффект в электронных приборах и другие явления.Тогда

.

Вместо мощности Р_Ш можно рассмотреть энергию шума G_Ш , причем

G_Ш = 4 k N Т.

Если исходить из того, что энергия полезного сигнала Р × t, где Р — мощность, a t — время измерения, должна быть боль­ше энергии шума, то возможность выполнения измерений на молекулярном уровне будет ограничиваться требованием выполнения неравенства

Р × t 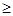G_Ш .

Используя различия в статистической природе шумов и полезных сигналов, во многих случаях удается преодолеть ограничения, обусловленные законами термодинамики. В частности, не когерентность шума позволяет при многократ­ном измерении, накоплении, оптимальной фильтрации и пу­тем использования других приемов обеспечить выполнение

измерений при отношении .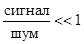

Принциальные ограничения следующего уровня обуслов­лены дискретностью измеряемых величин (нельзя, например, измерить заряд, меньший заряда электрона) или флюктуация­ми, определяемыми дискретностью вещества и энергии. Точ­ность измерений на этом уровне ограничивается законами квантовой механики.

Формальным отражением выхода на квантовомеханический уровень точности измерений служит появление в ма­тематическом описании факторов, которыми нельзя пренеб­регать, постоянной Планка h = 6,63ּ10 ^{- 34} Дж/Гц. Одним из таких факторов является принцип неопределенности Гейзенберга, связывающий (через постоянную Планка) точность измерения координаты и импульса частицы, времени и энер­гии, а также других пар физических величин. Точность измерений в таких условиях становится предметом разум­ного компромисса.

8.2. ОПРЕДЕЛЕНИЕ ТОЧНОСТИ ИЗМЕРЕНИЙ РАСЧЕТНЬМ ПУТЕМ

Потенциальная точность измерений, определяемая на любом уровне развития науки и техники точностью госу­дарственных эталонов, в обиходе недостижима. Поэтому естественно встает вопрос о реально достижимой точности измерений. При решении этого вопроса всегда исходят из анализа конкретной измерительной задачи и стараются, как можно полнее учесть всевозможные ограничения.

Пусть, предположим, apriori известно, что сигнал X(t) на выходе линейного измерительного преобразователя с ко­эффициентом преобразования, равным 1, будет представлять собою смесь полезного сигнала X(t) = Q = const и шумовой помехи N(t) в виде нормального стационарного случайного процесса со средним значением, равным нулю, обусловлен­ной внешними и внутренними влияющими факторами. Воз­можны следующие способы измерения неизвестного значе­ния Q:

усреднение Х (t) по времени (в течение одной реализа­ции);

усреднение Х (t) по множеству значений, относящихся в каждой реализации к одному и тому же моменту вре­мени;

усреднение Х (t) и по множеству, и по времени. Наряду с этим метрологическое обеспечение измерений мо­жет быть организовано по-разному. В одном из вариантов (см. рис. 161, а) информация о размере единицы передает­ся только измерительному преобразователю. В этом слу­чае в сигнал на выходе измерительного преобразователя

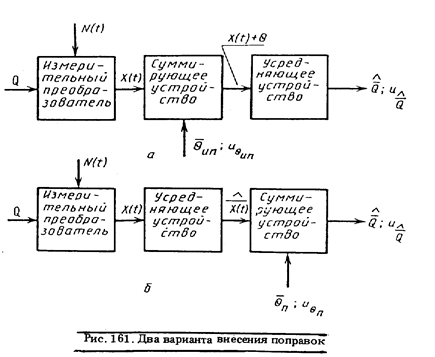
может вноситься поправка. Точное значение ее обычно не­известно, что учитывается ситуационной моделью поправ­ки. Усредняющее устройство затем выполняет необходимые математические операции.

Во втором варианте информация о размере единицы пе­редается измерительному прибору в целом, включающему в себя и измерительный преобразователь и усредняющее устройство. Поправка в таком случае вносится при необ­ходимости в показание прибора— рис. 161, б.

Показателем точности служит аналог стандартного откло­нения результата измерения 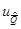. Выражения для него при­ведены в табл. 50, где — дисперсия шумовой помехи;

— аналог среднего квадратического отклонения в ситуа­ционной модели поправки; 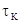— интервал корреляции нор­мального стационарного случайного процесса Х (t) ; Т_P — дли­тельность реализации того же процесса; п — число реализа­ции. При составлении табл. 50 учтено, что в первом ва­рианте поправка вносится в мгновенные значения X(t) с последующим цифровым усреднением полученного массива. Поправка на неточность дискретного усреднения имеет дисперсию .

Табл. 50 позволяет проанализировать зависимость точ­ности измерений от множества факторов. Так, например, очевидна зависимость точности от объема экспериментальных данных (п, Тр). Ограничение объема экспериментальных дан­ных ограничивает точность измерений. Видна зависимость точности от конструктивных и схемотехнических решений (способа усреднения, значения ). Есть возможность аль­тернативного выбора, а в случае ограничений на выбор — непосредственного расчета точности измерений. Двумя вариантами представлены подходы к метрологическому обеспечению, качество которого определяется значениям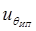и и 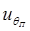. Весьма наглядна зависимость точности от априорной

ной информации о влияющих факторах ( , 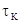). Если точ­ной информации о параметрах помехи нет, а известен лишь закон распределения их вероятности, то

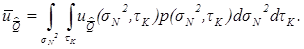
При 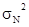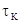р( 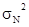, ) = р( ) р( 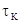) этот двойной интеграл в каж­дом конкретном случае вычисляется просто.

По табл. 50 в каждом конкретном случае легко найти минимальное значение 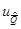, т.е. определить максимально воз­можную точность при выбранных условиях и ограничениях.

Подобным образом рассчитывается и анализируется точ­ность измерений и в более сложных случаях, отличающих­ся тем, что приходится учитывать большее количество фак­торов.